Скалярное произведение векторов

Конспект урока

Скалярное произведение векторов

Урок 27. Скалярное произведение векторов

Цели урока:

• Ввести понятия угла между векторами и скалярного произведения векторов

• Сформулировать и доказать необходимое и достаточное условие произведения

векторов

• Воспитывать математическую культуру

• Развивать интерес к математике

Ход урока

1. Организационный момент.

Учащимся сообщается тема и план урока.

1. Повторение. Проверка домашнего задания

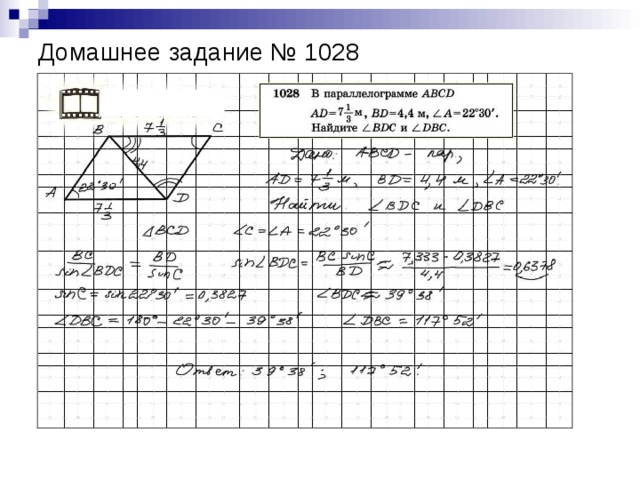
Проверить № 1028 из домашней работы. Учитель вызывает двоих учащихся : один решает № 1028, другой задачу под № 6. Остальные отвечают на вопросы.

1. Что называется вектором? Как изображается нулевой вектор?

2. Что мы называем длиной вектора?

3. Чему равна длина нулевого вектора?

4. Какие два вектора наз. коллинеарными, сонаправленными, противоположно

направленными?

1. Какие два вектора наз. равными?

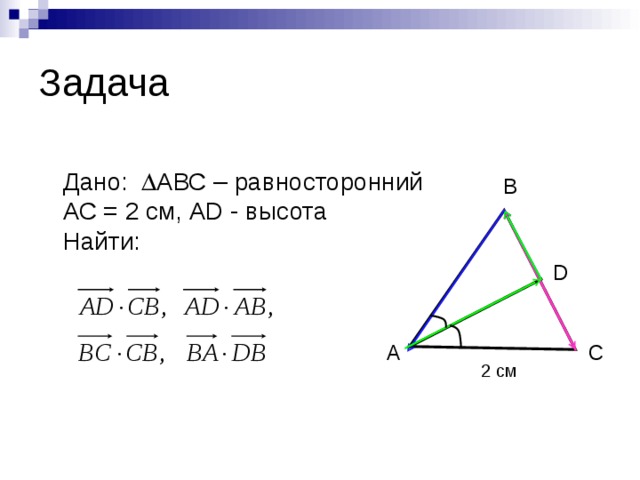
2. Решите задачу:  АВС – равносторонний, со стороной 2 см, АD - высота. Найдите

длину вектора .

1. Какие действия над векторами вы знаете?

1. Изучение нового материала.

Учитель в лекционной форме излагает теоретический материал по теме «Угол между векторами», опираясь на слайды №№ 1 – 4.

Учитель. Сегодня мы изучим еще одно действие над векторами: скалярное произведение векторов. Это понятие тесно связано с таким понятием как угол между векторами, поэтому мы сначала изучим это понятие.

Слайд 2. (Анимация на слайде позволяет продемонстрировать построение угла между векторами в случае не сонаправленных векторов)

Пусть даны два вектора и . Рассмотрим сначала, случай, когда векторы не являются сонаправленными. От произвольной точки О отложим векторы , . Лучи ОА и ОВ образуют угол АОВ. Градусную меру этого угла обозначим буквой  и будем говорить, что угол между векторами и равен . Угол между векторами и обозначается так( , ).

Слайд 3. (используя этот слайд учитель вводит понятие угла между сонаправленными векторами и понятие перпендикулярных векторов)

Если векторы а и b сонаправлены, в частности один из них или оба нулевые, то угол между векторами равен 0°.

Два вектора называются перпендикулярными, если угол между ними равен 90°.

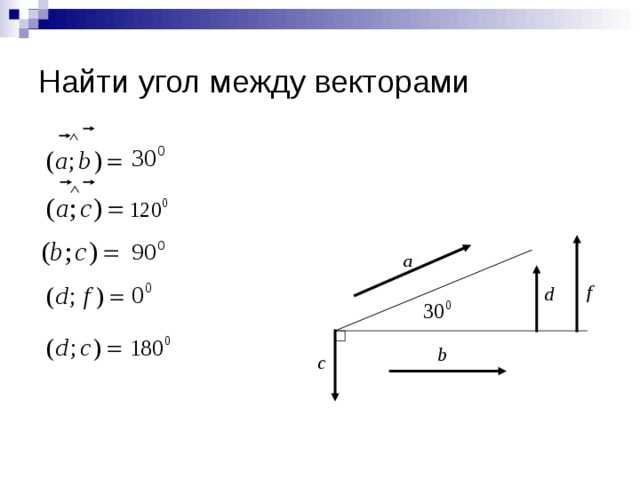
Слайд 4. Найдите углы между векторами указанными на слайде.

Слайд 5.

Используя данный слайд, учитель вводит определение скалярного произведения векторов и приводит пример вычисления скалярного произведения векторов. Учащиеся записывают в тетрадь.

Далее учащиеся под руководством учителя решают задачу на нахождение скалярного произведения векторов, отраженную на слайде 6.

Слайд 6

При решении задачи учитель обращает внимание учащихся на результат скалярного произведения векторов . Обсуждается вопрос, почему скалярное произведение оказалось равным нулю. При выполнении какого условия скалярное произведение ненулевых векторов будет равно нулю? Справедливо ли обратное утверждение?

Далее используя слайды

№№ 7,8,9 учитель формулирует и доказывает необходимое и достаточное условие равенства нулю скалярного произведения векторов, вводит понятие скалярного квадрата.

Слайд 7

Слайд 8 (доказательство на слайде появляется поэтапно, что позволяет учителю

с помощью наводящих вопросов учащимися самим прийти к доказательству)

Слайд 9

Выполнить задание из учебника № 1050

Решение:

5. Подведение итогов. Домашнее задание.

Слайд 10

Слайд 12

Домашнее задание № 1028

Скалярное произведение векторов

Угол между векторами

О – произвольная точка

А

 АОВ = 



В

О

= 

3

Угол между векторами

• Если векторы и сонаправлены, в частности один из них или оба нулевые, то угол между векторами равен 0 °.
• Два вектора называются перпендикулярными , если угол между ними равен 90°

= 0 °

= 0 °

= 90 °

4

Найти угол между векторами

5

Скалярное произведение векторов

Определение. Скалярным произведением векторов называется произведение их длин на косинус угла между ними

Пример:

Задача

Дано:   АВС – равносторонний

АС = 2 см, АD - высота

Найти:

В

D

А

С

2 см

Необходимое и достаточное условие равенства нулю скалярного произведения

Скалярное произведение ненулевых векторов равно нулю тогда и только тогда когда эти векторы перпендикулярны

Скалярный квадрат

Скалярное произведение

называется скалярным квадратом вектора

Свойство.

Скалярный квадрат вектора равен квадрату его длины.

Самое главное

• Скалярным произведением векторов называется произведение их длин на косинус угла между ними
• Скалярное произведение ненулевых векторов равно нулю тогда и только тогда когда эти векторы перпендикулярны
• Скалярное произведение вектора самого на себя называется скалярным квадратом вектора
• Скалярный квадрат вектора равен квадрату его длины.

Применение скалярного произведения в физике

• Работа А постоянной силы F при перемещении тела из точки М в точку N, равна произведению длин векторов силы и перемещения на косинус угла между ними.
• Т.е. работа силы F равна скалярному произведению векторов силы и перемещения

Домашнее задание

• Пп. 101-102
• № 1040
• № 1041
• № 1042