Система работы по подготовке учащихся к огэ по математике.

СИСТЕМА РАБОТЫ ПО ПОДГОТОВКЕ УЧАЩИХСЯ

К ОГЭ ПО МАТЕМАТИКЕ.

Государственная итоговая аттестация по математике в 9 классе – это результат работы ученика и учителя на протяжении пяти лет обучения в школе, и подготовка к ней является важной составляющей учебного процесса.

Принимая учащихся в 5 класс от разных учителей начальных классов, иногда с низким темпом продвижения в обучении, испытывающих затруднения при усвоении нового материала, имеющих пробелы в знаниях, учитель вынужден решать сложную педагогическую задачу: достижения всеми учениками уровня обязательных результатов обучения. В этих условиях ориентация на максимальный объем усвоения учебного материала приводит к заметной перегрузке более слабых учащихся. Они находятся в дискомфортном положении не справляющихся с учебой; развивается чувство собственной неполноценности, которое по законам психологии требует вытеснения, поиска удовлетворения в других сферах.

Выходом из этой ситуации является дифференцированный подход к обучению учащихся на основе выделения уровня математической подготовки, обязательного для каждого ученика школы, при этом ограничение требований к части учащихся, связанное с ориентацией на обязательный минимум знаний, не означает ослабления учебной дисциплины или снижения требовательности к сильным учащимся.

Успешнее сдает экзамен тот, кто

• в полном объеме владеет материалом,

• хорошо знаком с процедурой проведения экзамена,

• психологически готов к экзамену и адекватно реагирует на нестандартные ситуации.

Задача учителя помочь ученику как можно лучше решить первые две проблемы, и уменьшить, насколько это возможно, третью. Экзамен в новой форме не похож на обычные школьные контрольные, к которым привыкли и ученики, и учителя, и родители. Именно поэтому к нему надо специально готовить даже тех, кто неплохо пишет обычные контрольные работы, а уж тем более тех, кто испытывает затруднения в математике.

Для того чтобы достичь хороших результатов, нужно:

1) на каждом уроке проводить обязательный устный счет;

2) включать в изучение текущего учебного материала задания, соответствующие экзаменационным, которых нет в учебнике;

3) в содержание текущего контроля включать экзаменационные задачи;

4) итоговое повторение строить исключительно на отработке умений и навыков, необходимых для получения положительной отметки на экзамене;

5) изменить систему контроля над уровнем знаний учащихся по математике.

При подготовке учащихся к государственной итоговой аттестации по математике за курс основной школы в новой форме необходимо придерживаться следующих рекомендаций:

1. Начинать подготовку к ОГЭ по математике надо с арифметики. Даже способный ученик, набирающий в итоге максимальные баллы, допускает от недостатка внимания к вычислениям не вынужденные ошибки, а на первых уроках иногда даже путается со сложением дробей, положительных и отрицательных чисел. Большой вред арифметическим навыкам наносит использование микрокалькулятора при выполнении домашних заданий, а без них невозможно изучение таких понятий, как корни, степени, квадратные и даже линейные уравнения и т.д.

2. Главная цель работы любого учителя – научить ученика самостоятельно решать задачу, проанализировать ее:

• за нестандартной формулировкой увидеть алгоритм или несколько алгоритмов решения;

• четко видеть, что известно и что из этого можно найти (что нужно найти в задаче и что для этого должно быть известно);

• прикинуть количество ответов, а так же в каких пределах они находятся;

• записать решение;

• проконтролировать его правильность проверкой, если это возможно;

• записать ответ, в соответствии с основным вопросом;

• если это задание с выбором ответа, то исключить те варианты, которые категорически не подходят, а далее либо решить, либо сделать логическое заключение.

Читая условие, ученик должен видеть ситуацию, которая ему предлагается, а, решив задачу, четко ответить на поставленный вопрос.

3. Некоторые задания, входящие в экзаменационную работу, отличаются по форме от стандартных упражнений, содержащихся в популярных учебниках по алгебре и геометрии, а по некоторым заданиям в учебниках представлено недостаточное количество упражнений.

В первой части работы такими «непривычными» заданиями являются задания, в которых предлагается:

• выразить из формулы одну величину через другие;

• выполнить действия с числами, представленными в стандартном виде (на эту тему отводится всего 2 урока алгебры в 8 классе);

• проанализировать графические зависимости, отражающие реальные процессы (речь идет не о заданиях, где туристы ушли в поход, а потом вернулись обратно, а о заданиях, где по графику надо определить, кто из кандидатов получил больше голосов в период с 20-й до 40-й минуты);

• ответить на вопросы по теории вероятностей.

Во второй части работы следует обратить внимание на задания по теме «Прогрессии», а также на задания, в которых предлагается исследовать, при каких значениях k прямая пересекает в трех различных точках график функции, которая задана кусочно. Некоторые задания предполагают знание формул из курса физики, и умение выражать рассматриваемые величины в разных единицах измерения. Самым сложным заданием является геометрическая задача (№ 26).

4. В экзаменационную работу включено 9 заданий по геометрии (6 заданий в первой части и 3 задания во второй части). Поскольку геометрию в школе проходят по остаточному принципу, ей надо уделить особое внимание. Начиная изучать геометрию в 7 классе, дети, зачастую, сталкиваются с рядом трудностей и непонимания требований к ним. Ведь до 7 класса они привыкли видеть другую математику. Бόльшая часть школьников не любит этот предмет из-за необходимости выучивать наизусть немалое количество теорем, а без знания теории невозможно научиться решать геометрические задачи. Поэтому многие школьники путают медиану, биссектрису и высоту, не знают определение синуса и косинуса в прямоугольном треугольнике, не умеют вычислять площадь треугольника, не видят сходственные стороны в подобных треугольниках. Эти термины и определения необходимо повторять во время дополнительных занятий и на индивидуальных консультациях.

5. Обязательное знание правил, формул, теорем. Проводить опросы, проверки знаний обучающихся теоретических фактов во время

• уроков;

• во внеурочное время в виде зачетов.

6. В устной работе (проводить на каждом уроке), кроме заданий, соответствующих теме урока, использовать задания вычислительного характера и задания, связанные с особо трудно усваиваемыми темами:

• действия с дробями,

• процентами,

• графиками функций,

• решение геометрических задач по готовым чертежам.

7. В каждом классе есть темы, которые являются основополагающими и очень важными, например,

• тема решения квадратных уравнений в 8 классе;

• теорема Пифагора в 8 классе;

• площади фигур.

Надо стараться подвести восьмиклассников к изучению этих тем таким образом, чтобы у них не возникал вопрос «Почему?» эта тема так важна. Учащимся 8 класса можно предложить ознакомиться с вариантами ОГЭ, и вычленить вместе с ними ряд заданий, для выполнения которых необходимы умения решать квадратные уравнения. На уроках геометрии необходимо проводить подобную работу: выделять задания, наиболее часто встречаемые на экзаменах.

8. Включать в содержание урока не только решение основных заданий по теме, но и дополнительные вопросы, тем самым, обобщая и связывая между собой различные темы, и повторяя одновременно.

9. Подбирать задания, вызывающие трудности у учащихся, и постоянно решать на уроках эти задания:

• неполные квадратные уравнения,

• квадратные неравенства,

• упрощение степеней с разными основаниями,

• задания с арифметическим квадратным корнем,

• применение свойств касательной к окружности,

• подобие фигур.

10. Увеличить количество рассматриваемых на уроке и предлагаемых на дом заданий на чтение графиков и графических соответствий.

11. Уделять больше внимания разделу «Числовые функции и их графики», расширив подборку заданий:

• на построение графиков элементарных функций в общем виде;

• на исследование функций в зависимости от коэффициентов (в том числе и обратные задания);

• на построение графиков функций, область определения которых ограниченное множество.

12. При решении уравнений и систем уравнений использовать чаще задания графического плана. Ученик должен четко представлять связь между аналитической записью уравнения, неравенства, системы уравнений и их графической интерпретацией.

13. Использовать различные формулировки одного и того же задания, предлагая учащимся составление новых формулировок по заданному условию, а также восстановление условия задания по первым строкам его решения.

14. При решении задач с помощью уравнений:

-принимать за переменную различные величины, данные в условии задачи,

-составить задачу по уравнению.

15. При изучении прогрессий обратить внимание на возможность вычислений только по определению.

16. Подбирать задания, содержащие более одного вопроса.

17. Требовать от учащихся записи ответа в каждом задании.

18. Включать вопросы курса теории вероятностей, как в устную, так и в письменную работу на уроках математики.

19. Как можно больше использовать упражнений на выражение одной переменной через другую.

20. При решении уравнений, неравенств и систем уравнений обозначать переменные не только х и у, но и другими буквами. Решив уравнение, обязательно выполнять проверку.

21. Выполняя действия со степенями, работать с числовыми значениями, включая числа, записанные в стандартном виде.

22. В заданиях вычислительного характера, использовать запись ответа в стандартном виде или в виде десятичной дроби.

23. Координировать работу с учителями физики и химии по практическому использованию знаний, приобретенных учащимися на уроках математики, при различных вычислениях и решениях задач.

24. Особое внимание на уроках необходимо уделять повторению, которое должно проводиться постоянно, как сопутствующее новому материалу, так и тематическое. При повторении и изучении нового материала следует учитывать рекомендации психологов: материал хорошо запоминается, если его повторять на 3, 7 и 11 уроках после объяснения.

25. В течение всего учебного года в контрольные и самостоятельные работы обучающего характера следует включать различные формы заданий: задания работы с выбором ответа, с кратким ответом, а также стандартные для математики задания, в которых необходимо дать развернутое решение с полным объяснением.

26. В процессе выполнения обучающих работ нужно отрабатывать процедурные моменты экзамена в новой форме: организация работы в присутствии учителя, не работающего в классе, распределение времени при решении заданий, исправление ответов на задания в бланках. Знакомить с инструкцией по выполнению экзаменационной работы заранее.

27. Необходимо неоднократно напоминать ученикам, что на экзамене следует

-выполнять задания первой части работы сначала в тестах или на черновиках, а потом обязательно перенести все ответы в бланк, при этом ответы в бланке можно исправить;

-при выполнении заданий второй части работы сначала записать решения на черновике, а затем аккуратно перенести их в бланк №2, если недостаточно бланка №2, то организатор выдаст дополнительный бланк №2.

28. Следует учить школьника «технике сдачи теста». Эта техника включает в себя следующие моменты:

-Обучение постоянному жёсткому контролю времени, особенно это касается высокобальников. На консультациях, пробных и репетиционных тестированиях необходимо постоянно обращать внимание учащихся на то, сколько времени необходимо тратить на то или иное задание. Например, если на выполнение первой части (20 заданий) рекомендован 1 час, то на выполнение одного задания необходимо затратить не более 3 минут, а остальные 3 часа посвятить второй части работы. Выдержать этот график может только тот, кто приучен 3 – 4 часа заниматься математикой с полной отдачей. Отсутствие привычки «напрягаться» в математике несколько часов подряд – одна из причин низкого качества выполнения работы. Интеллект, как и мышцы, нужно постоянно тренировать – от этого он только сильнее становится. Поэтому нужно постоянно повышать нагрузки и скорость выполнения заданий.

-Обучение оценке объективной и субъективной трудности заданий. Ученики обычно сами знают, какие задания для них являются наиболее сложными. Таких «слабых» мест следует избегать при выполнении теста. Сначала нужно выполнять задания, в которых школьник ориентируется хорошо. Задача учителя состоит в том, чтобы школьник самостоятельно сумел набрать максимально возможное для него количество баллов, поэтому изречение «лучше меньше, да лучше» здесь оказывается вполне справедливым.

-Обучение прикидке границ результатов, анализу ответа на предмет соответствия действительности, минимальной подстановке как приёму проверки ответа. Следует учить школьников простым для проверки результатов сразу, а не «если останется время». Необходимо после решения задания приучать учеников внимательно перечитывать условие и вопрос (что нужно было найти?). Поскольку в учебниках дополнительных действий с ответами (например, найти сумму корней, а не сами корни) практически не встречается, многие школьники не обращают на них внимания, записывая при верно решённом задании неправильный ответ.

- Необходимо учить технике выбора ответа методом «исключения» явно неверного ответа. Особое внимание следует уделять заданиям, в которых формулировка звучит как «Выберите из данных выражений те, которые можно (или нельзя) преобразовать к виду…..». Самое главное здесь обратить внимание на ключевые слова «можно» или «нельзя», иначе ответ может получиться совершенно противоположным.

- Обучение приёму «спирального движения» по тесту. Ученик, просматривая тест от начала до конца, отмечает для себя задания, которые кажутся ему простыми и понятными и выполняются сходу, без особых раздумий. Именно их школьник выполняет первыми. Затем необходимо «пробежать» глазами вторую часть работы и отметить 1-2 задания, которые поняли сразу, в этой части есть задания (например, № 21), которые «средний» ученик решает без особого напряжения. К ним можно перейти, когда будет в основном закончена первая часть работы. Затем можно перейти вновь к первой части работы и попробовать выполнить задания, которые не «поддались» сразу. Если ученик не может и после этого выполнить какое-то задание первой части, то после контроля времени (3-4 минуты), следует перейти к другому заданию сначала первой части, а затем второй части работы. Так необходимо делать несколько раз «по спирали» и делать то, что «созрело» к данному моменту.

29. Может помочь при подготовке обучающихся к экзамену Интернет. Следует предлагать учащимся тренировочные задания, тесты и зачеты в режиме онлайн. Если ученики хотят в комфортных условиях (за чашечкой чая, в любимом кресле и т.п.) подготовиться к ОГЭ, они могут выбрать Интернет-курсы. Получив регистрационные данные (логин и пароль), они делают это в любое удобное для них время заходят на Учебный сервер, где размещены:

• теоретические материалы к каждому типу заданий;

• разбор каждого типа заданий;

• задания, которые вызывают наибольшие трудности (по результатам анализа статистических материалов);

• электронный тренажер;

• контрольное тестирование;

• рекомендации по подготовке к ОГЭ;

• учебный сервер позволит им консультироваться с преподавателем в Online и Offline режимах.

Для учеников, у которых дома нет Интернета, можно организовать работу в школьном компьютерном классе. Работу учащихся необходимо контролировать, консультируя их по заданиям, в решении которых они испытывают трудности.

30. Школьный психолог должен побеседовать со всеми выпускниками при подготовке к экзаменам.

Необходимо добиться того, чтобы каждый ученик к окончанию 9 класса представлял полностью материал, предлагаемый на экзамене, и был готов психологически к такому достаточно серьезному испытанию, как экзамен, а для этого необходима целенаправленная и систематическая подготовка.

Важным условием успешной подготовки к экзаменам является тщательное отслеживание результатов учеников по всем темам и своевременная коррекция уровня усвоения учебного материала.

В апреле 2013 года мною была проведена диагностическая контрольная работа в форме ГИА в 8^а,б классах. По результатам выполнения работы учащиеся были поделены на группы в соответствии с тремя уровнями подготовки. При этом обучающиеся знали, что по мере усвоения материала, коррекции знаний, они могут переходить в следующую по уровню подготовки группу.

Обучающиеся, имеющие средний уровень математической подготовки, могут без особого труда усваивать программный материал на уроке, практически всегда справляются с предложенными заданиями, получая удовлетворительные отметки.

Дети с повышенной мотивацией к обучению математике без труда овладевают материалом, проявляют интерес к изучению предмета. С ними необходимо строить работу, проводя индивидуальные консультации после уроков (Приложение 2). Именно им рекомендовать использование Интернет-ресурсов для самостоятельной домашней подготовки к экзамену. На уроках предлагать индивидуальные карточки с элементами тестирования, как на закрепление нового материала, так и для выполнения домашнего задания. Практиковать с высокобальниками на уроке самостоятельную работу в группе по доказательству новой теоремы или решению нестандартной задачи – «мозговой штурм». Главная цель каждого учителя по работе с такими детьми – во время уроков и, органично дополняя их внеурочными занятиями, систематизировать и углублять знания по предмету для успешной сдачи выпускных экзаменов.

В группе «риска» – слабоуспевающие ученики. Им не всегда удаётся справиться с предлагаемыми заданиями в классной и домашней работе. С этими ребятами надо заниматься дополнительно после уроков (Приложение 1). Отрабатывать те задания, которые вызывают у них затруднения. «Натаскивать» их примерами и задачами подобного характера. Эти меры необходимы, для преодоления ими «нижнего порога» на ГИА.

Разработана система контроля знаний, умений и навыков обучающихся, которая позволяет:

1) постоянно получать информацию об уровне усвоения учебного материала по каждой теме;

2) своевременно принимать меры по восполнению пробелов;

3) повысить уровень познавательных способностей учащихся;

4) повысить мотивацию учащихся к учебе;

5) развивать навыки самостоятельной деятельности учащихся;

6) привлечь внимание родителей непосредственно к учебному процессу, повысить их ответственность за обучение детей.

В систему контроля включены диагностические карты (приложение 3), а также зачетные книжки учеников (приложение 4). В зачетной книжке перечисляются темы, предусмотренные кодификатором требований к уровню подготовки выпускников по математике, все запланированные проверочные работы, которые определяют уровень усвоения учащимися базовых знаний по данной теме. После проведения проверочной работы в зачетную книжку выставляется отметка.

Если ученик получил неудовлетворительную оценку, ему предоставляется возможность поработать над ошибками и затем обязательно пересдать проверочную работу. После каждой работы зачетная книжка дается на подпись родителям. В книжке также указывается дата дополнительных занятий. Зачетная книжка предоставляет родителям возможность следить за подготовкой к диагностической работе, своевременно принимать меры по коррекции знаний учащегося.

Подготовка ко второй части контрольно-измерительных материалов и государственной итоговой аттестации осуществляется как на уроках, так и во внеурочное время на дополнительных занятиях. При этом используются сборники для подготовки к экзаменам, рекомендованные ФИПИ и МИИО.

Ключевым моментом по подготовке к ОГЭ является ведение «Тематических тетрадей» по темам в соответствии с «Кодификаторами элементов содержания и требований к уровню подготовки выпускников основной школы». Такой приём позволяет иметь всю информацию в одном месте и вместе с тем даёт возможность быстро находить нужный раздел.

График посещения групповых дополнительных занятий с обучающимися 9^а,б классов

по подготовке к итоговой аттестации по математике

Группа «риска» (базовый уровень)

№ п/п	Список обучающихся	Класс	Д а т а
1		9а
2		9а
3		9а
4		9а
5		9а
6		9а
7		9а
8		9а
9		9а
10		9б
11		9б
12		9б
13		9б
14		9б
15		9б
16		9б
17		9б
18		9б
19		9б
20		9б
21		9б
Т е м а занятия

Приложение 2

График посещения групповых дополнительных занятий с учащимися 9^а,б классов

по подготовке к итоговой аттестации по математике

№ п/п	Список обучающихся	Класс	Д а т а
1		9а
2		9а
3		9а
4		9а
5		9а
6		9а
7		9а
8		9а
9		9а
10		9а
11		9б
12		9б
13		9б
14
15
16
17
18
19
20
21
22
23
24
25
Т е м а занятия

Приложение 3

Диагностическая карта подготовки к государственной итоговой аттестации по математике ученика 9^аб класса

Ф.И.

Группа «риска»

Проверяемые навыки
Числа и вычисления	Сравнение рациональных чисел	Действия с обыкновенными дробями		Действия с десятичными дробями			Степень с целым показателем
Задачи	Задачи на проценты	Составление буквенного выражения по условию задачи		Составление уравнений по условию текстовой задачи			Текстовые задачи
Алгебраические выражения								Действия с алгебраическими дробями
	Область определения выражения	Числовые подстановки в буквенные выражения		Преобразование целых выражений (формулы)
	Квадратные корни	Выражение из формул одной величины через другие		Разложение многочлена на множители			Степень с целым показателем
Уравнения и неравенства	Уравнения
	Линейные	Квадратные		Дробно-рациональные			Система линейных уравнений
	Неравенства
	Свойства неравенств	Линейные		Квадратные			Система линейных неравенств
Числовые последовательности	Арифметическая прогрессия				Геометрическая прогрессия
	Формула общего члена	Формула суммы первых членов		Формула общего члена			Формула суммы первых членов
Функции	линейная	квадратичная		у = kx, у = k/x			Интерпретация графика реальной зависимости
Геометрия	Треугольник	Многоугольники		Окружность и круг			Векторы
Статистика и теория вероятностей	Описательная статистика		Вероятность			Комбинаторика

Приложение 4

ЗАЧЕТНАЯ КНИЖКА

учащегося 9^аб класса по подготовке

к государственной итоговой аттестации

по математике

1. Выполнение самостоятельных, контрольных работ

Группа «риска»

Дата

Тема проверочной работы

Номер задания

Баллы

Оценка

1

2

3

4

5

6

7

8

9

10

С. р. по теме «Деление многочленов»

С. р. по теме «Алгебраические уравнения»

С. р. по теме «Системы уравнений»

Контрольная работа № 1 по алгебре по теме «Алгебраические уравнения. Системы нелинейных уравнений»

С. р. по теме «Степень с целым показателем»

С. р. по теме «Свойства арифметического корня»

С. р. по теме «Степень с рациональным показателем»

Контрольная работа № 2 по алгебре по теме «Степень с рациональным показателем»

Опрос теории по теме «Соотношения между сторонами и углами треугольника»

С. р. по теме «Функция»

С. р. по теме «Решение треугольников»

Контрольная работа № 3 по алгебре по теме «Степенная функция»

С. р. по теме «Элементы тригонометрии»

Опрос теории по теме «Правильные многоугольники»

С. р. по теме «Арифметическая прогрессия»

Опрос теории по теме «Длина окружности и площадь круга»

С. р. по теме «Геометрическая прогрессия»

Контрольная работа № 4 по алгебре по теме «Прогрессии»

Контрольная работа № 3 по геометрии по теме «Длина окружности и площадь круга»

Практическая работа по теме «Движения»

Контрольная работа № 4 по геометрии по теме «Движения»

Контрольная работа № 5 по алгебре по теме «Случайные события. Случайные величины»

Многогранники»

Годовая контрольная работа

2. Выполнение диагностических контрольных работ

№ задания	Проверяемые элементы математической подготовки	Школьный этап	Школьный этап	Школьный этап	Школьная ДКР апрель
1	Умение выполнять арифметические действия с рациональными числами
2	Умение сравнивать рациональные числа
3	Владение понятием квадратного корня
4	Решение линейных уравнений
	Решение квадратных уравнений
	Решение систем линейных уравнений
5	Представление о графиках линейной, квадратичной и степенной функций
6	Владение понятием арифметической прогрессии
	Владение понятием геометрической прогрессии
7	Преобразование целых выражений (с использованием формул сокращенного умножения)
	Выполнение действий с алгебраическими дробями
8	Решение линейных неравенств с одной переменной
	Решение квадратных неравенств
	Решение систем линейных неравенств
9	Уметь выполнять действия с геометрическими фигурами
10	Уметь выполнять действия с геометрическими фигурами
11	Уметь выполнять действия с геометрическими фигурами
12	Уметь выполнять действия с геометрическими фигурами
13	Умение оценивать логическую правильность рассуждений, распознавать ошибочные заключения
14	Статистика
15	Интерпретация графика реальной зависимости
16	Решение задач на проценты
17	Геометрия с практическим содержанием
18	Статистика
19	Теория вероятностей
20	Составление алгебраических выражений, формул по условию задачи
	Выражение из формул одной величины через другие
Количество набранных баллов
Процент выполнения
Оценка
Родители ознакомлены

3. Работа с родителями

Дата	Форма работы	Подпись

4. Посещение индивидуальных дополнительных занятий,

проведение индивидуальных консультаций

Дата	Тема	Вид работы	Отметка

3
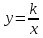