Цель: закрепить понятие неравенства с одной переменной, закрепить умения и навыки решать данные неравенства.
План урока:
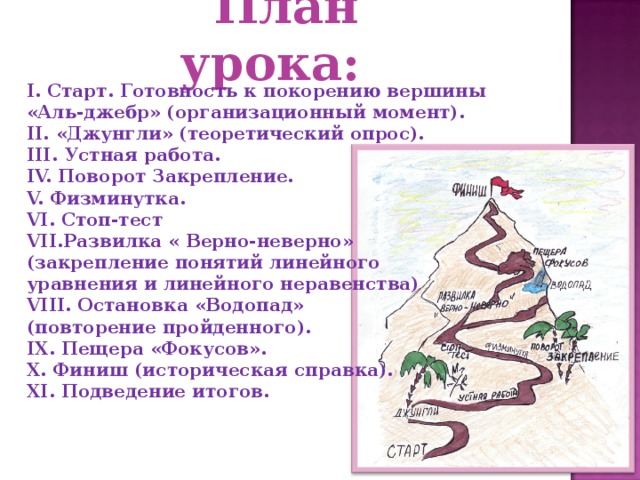
I. Старт. Готовность к покорению вершины «Аль-джебр» (организационный момент).
II. «Джунгли» (теоретический опрос).
III. Устная работа.
IV. Поворот Закрепление.
V. Физминутка.
VI. Стоп-тест
VII. Развилка « Верно-неверно»
(закрепление понятий линейного
уравнения и линейного неравенства)
VIII. Остановка «Водопад»
(повторение пройденного).
IX. Пещера «Фокусов».
X. Финиш (историческая справка).
XI. Подведение итогов.
ДЖУНГЛИ
- Дать определение линейного неравенства с одной переменной. Что значит решить неравенство?
- Дать определение линейного неравенства с одной переменной.
- Что значит решить неравенство?
3. Равносильные неравенства - это…….
4. Перечислите свойства решения неравенств.
- 3. Равносильные неравенства - это……. 4. Перечислите свойства решения неравенств.
Работа по учебнику с. 183 №859 (б, г, е).
- При каких значениях переменной выражение имеет смысл?
2. Какие свойства вы использовали при решении неравенств?
Быстро встали, улыбнулись.
Выше-выше потянулись.
Ну-ка, плечи распрямите,
Поднимите, опустите.
Вправо, влево повернитесь,
Рук коленями коснитесь.
Сели, встали. Сели, встали.
И на месте побежали.
0 1) б) x -5≤0 2) в) 5- x 0 3) г) 5+ x ≥0 4) - 5 5 - 5 5 8" width="640"
Стоп-тест
1. Найдите множество решений каждого неравенства:
а) x +50 1)
б) x -5≤0 2)
в) 5- x 0 3)
г) 5+ x ≥0 4)
- 5
5
- 5
5
8
2. Найдите наибольшее целое число, удовлетворяющее неравенству
3-(1-2 y )
а) -1; б) 0; в) 1; г)2.
1 задание:
А – 3
Б – 4
В – 2
Г – 1
2 задание:
Б
3a-11 7b2a-4 9y-36 ВЕРНО НЕВЕРНО ВЕРНО НЕВЕРНО ВЕРНО" width="640"
Линейные неравенства с одной переменной
8 +5y≤21+6y
-¾x²
8(1-2a)3a-11
7b2a-4
9y-36
ВЕРНО
НЕВЕРНО
ВЕРНО
НЕВЕРНО
ВЕРНО
Остановка «Водопад»
Работа по учебнику
стр.183 №865
Ответ: меньше 2 см.
Пещера «Фокусов»
1. Задумайте число от 1 до 20 и запишите его в тетрадях.
2. Прибавьте к нему 5.
3. Результат умножьте на 3.
4. От того, что получилось, отнимите 15 и запомните ответ.
5. Назовите мне ответ и я отгадаю число, которое вы загадали.
Алгебра как искусство решать уравнения зародилась очень давно в связи с потребностями практики, в результате поиска общих приемов решения однотипных задач.
Слово «алгебра» возникло после появления трактата «Китаб аль-джебр валь-мукабала» математика и астронома Мухаммеда бен Муса аль-Хорезми ( 787- ок.850). Термин «Аль-джебр», взятый из названия этой книги, в дальнейшем стал употребляться как «алгебра».
Современная алгебра - один из основных разделов математики.
П. 34 стр. 199 №№ 940 (д,е), 941 (в,г)
