Уроки 40-41.
Тема урока: Квадратные неравенства. Решение квадратных неравенств.
Примеры решения неравенств второй степени с одной переменной.
Цели урока:
Научить решать неравенства второй степени с одной переменной.
Развивать логическое мышление, математическую речь, познавательный интерес к предмету.
Воспитывать прилежание, трудолюбие, аккуратность, точность.
План урока.
Актуализация знаний.
Постановка цели.
Изучение нового материала.
Закрепление изученного материала.
Обучающая самостоятельная работа.
Домашнее задание.
Подведение итогов.
Ход урока
1. Актуализация знаний.
– Какую функцию мы изучаем?
– Определение квадратичной функции.
– Давайте поработаем ,чтобы хорошо усвоить новый материал.
Математический диктант.
Что является графиком функции y=ax2+bx+c ?
От какого коэффициента зависит направление ветвей параболы?
Как определить координаты вершины параболы?
Запишите формулу нахождения дискриминанта квадратного уравнения.
Запишите формулу для нахождения корней квадратного уравнения.
Сколько корней имеет квадратное уравнение, если D0 ?
Сколько корней имеет квадратное уравнение, если D
Сколько корней имеет квадратное уравнение, если D=0 ?
- Обменяйтесь тетрадями и проверьте диктант соседа по парте.
2. Постановка цели.
– Мы с вами умеем строить график квадратичной функции, умеем решать квадратные уравнения, а сегодня мы должны научиться решать неравенства второй степени с одной переменной.
Запишем тему урока в тетрадь.
Квадратные неравенства
Изучение нового материала.
Задание 1. Какие из неравенств вы бы назвали неравенствами второй степени:
1) 6х2 – 13х0; 2) x2 – 3x – 140; 3) (5 + x)(x – 4)7;
4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() ;
;
7) 8x20; 8) (x – 5)2 – 250; 9) x(x – 9) – x20?
Определение: Неравенство, левая часть которого есть многочлен второй степени, а правая – нуль, называется неравенством второй степени.
Все квадратные неравенства могут быть приведены к одному из следующих видов:
1) ах2 + bx + c 0;
2) ах2 + bx + c 3) ах2 + bx + c 0;
4) ах2 + bx + c 0.
Определение: Неравенствами второй степени с одной переменной называют неравенства вида ах2 + вх + с 0 и ах2 + вх + с 0, где х – переменная, а, в и с – некоторые числа, причем а ≠ 0.
Решать такие неравенства мы будем с помощью нахождения промежутков, в которых соответствующая квадратичная функция принимает положительные или отрицательные значения.
Итак, выполним в тетрадях следующее задание:
Решить неравенство: 5х2 + 9х – 2 0.
Решение.
– Какая квадратичная функция соответствует данному неравенству:
1. у = 5х2 + 9х – 2
– Что является её графиком?
– Выясним, как расположена парабола относительно оси х.
– Как она может быть расположена (пересекать ось х, находиться выше оси х, ниже оси х, касаться оси х)?
– Как это определить?
2. Нули функции, у = 0.
5х2 + 9х – 2 = 0,
D = 81 + 40 = 121,
![]()
х1 = 0,2 , х2 = -2.
3. Покажем схематически, как расположена парабола в координатной плоскости.
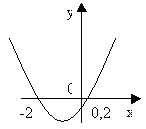
![]()
Запишем алгоритм решения неравенств второй степени с одной переменной.
1. Рассмотреть функцию, соответствующую данному неравенству, определить направление ветвей параболы.
2. Найти нули функции, т.е. абсциссы точек пересечения параболы с осью х, если они есть.
3. Изобразить схематически параболу в координатной плоскости.
4. Выбрать нужные промежутки.
5. Записать ответ.
Рассмотрим примеры 2, 3 и 4 в учебнике на странице 84. Сделаем соответствующие выводы.
4. Закрепление изученного материала.
Выполняем № 304 (1 столбик), 305, 306 (г, д, е), 308, 312 (б, в).
5. Обучающая самостоятельная работа.
Предлагается решить 3 неравенства, затем на доске показываются правильные ответы, для того, чтобы учащиеся могли проверить свои решения. Во время решения учащиеся консультируются с учителем. Те, кто успешно справится с решением, получат оценки.

Поднятием рук проверяем, как учащиеся усвоили новый материал.
6. Домашнее задание.
п.14, № 304 (2 ст), 306 (а,б,в), 309, 312 (а, г).
7. Подведение итогов.
– Какова была цель нашего урока?
– Сформулируйте определение неравенств второй степени с одной переменной.
– Как решать такие неравенства?
– Алгоритм решения.
Оценки за урок.
Задание 1. Какие из неравенств вы бы назвали неравенствами второй степени:
1) 6х2 – 13х0; 2) x2 – 3x – 140; 3) (5 + x)(x – 4)7;
4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() ;
;
7) 8x20; 8) (x – 5)2 – 250; 9) x(x – 9) – x20?
Алгоритм решения неравенств второй степени с одной переменной.
1. Рассмотреть функцию, соответствующую данному неравенству, определить направление ветвей параболы.
2. Найти нули функции, т.е. абсциссы точек пересечения параболы с осью х, если они есть.
3. Изобразить схематически параболу в координатной плоскости.
4. Выбрать нужные промежутки.
5. Записать ответ.

Задание 1. Какие из неравенств вы бы назвали неравенствами второй степени:
1) 6х2 – 13х0; 2) x2 – 3x – 140; 3) (5 + x)(x – 4)7;
4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() ;
;
7) 8x20; 8) (x – 5)2 – 250; 9) x(x – 9) – x20?
Алгоритм решения неравенств второй степени с одной переменной.
1. Рассмотреть функцию, соответствующую данному неравенству, определить направление ветвей параболы.
2. Найти нули функции, т.е. абсциссы точек пересечения параболы с осью х, если они есть.
3. Изобразить схематически параболу в координатной плоскости.
4. Выбрать нужные промежутки.
5. Записать ответ.






