

Прототипов заданий В12 – 25
Проверяемые требования (умения)
- Уметь строить и исследовать простейшие математические модели

Умения по КТ
- Моделировать реальные ситуации на языке алгебры, составлять уравнения и неравенства по условию задачи; исследовать построенные модели с использованием аппарата алгебры

Содержание задания В12 по КЭС
- Уравнения и неравенства . 2.1.8 Простейшие системы уравнений с двумя неизвестными 2.1.9 Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных 2.1.10 Использование свойств и графиков функций при решении уравнений 2.1.11 Изображение на координатной плоскости множества решений уравнений с двумя переменными и их систем 2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений 2.2.6 Системы неравенств с одной переменной 2.2.7 Равносильность неравенств, систем неравенств 2.2.8 Использование свойств и графиков функций при решении неравенств 2.2.9 Метод интервалов 2.2.10 Изображение на координатной плоскости множества решений неравенств с двумя переменными и их систем

Памятка ученику
Задание B12 - текстовая задача на движение или работу. Чтобы выполнить это задание, ученик должен составить и решить уравнение по условию, правильно интерпретировать полученный результат.

Прототип задания B12 (№ 26578)
- Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 24 км/ч, а вторую половину пути — со скоростью, на 16 км/ч большей скорости первого, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста. Ответ дайте в км/ч.
Примем путь за единицу, обозначим за х км/ч– скорость первого автомобилиста. Тогда скорость второго – (х+16) км/ч. Составим уравнение:
1/х=0,5/24+0,5/(х+16)
Корнями квадратного уравнения
х 2 -8х-768=0 являются числа-24 и 32.
Корень -24 не удовлетворяет условию задачи
Ответ: 32 км/ч.
Решение

Задания для самостоятельного решения
1) Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 42 км/ч, а вторую половину пути — со скоростью, на 28 км/ч большей скорости первого, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста. Ответ дайте в км/ч.
2) Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 27 км/ч, а вторую половину пути — со скоростью, на 18 км/ч большей скорости первого, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста. Ответ дайте в км/ч.
Ответ: 1)56 км/ч, 2)36 км/ч.
Проверка

Прототип задания B12 (№26581)
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 70 км. На следующий день он отправился обратно в А со скоростью на 3 км/ч больше прежней. По дороге он сделал остановку на 3 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч.
Примем за х км/ч – скорость велосипедиста из А в В., тогда его скорость на обратном пути составляет (х+3) км/ч
Составим уравнение:
70/х=70/(х+3)+3
Корнями квадратного уравнени:
х∙х+3х+70=0 являются числа:
-10 и 7. 7+3=10
Ответ: 10 км/ч.
Решение

Задания для самостоятельного решения
1) Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 154 км. На следующий день он отправился обратно в А со скоростью на 3 км/ч больше прежней. По дороге он сделал остановку на 3 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч.
2) Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 77 км. На следующий день он отправился обратно в А со скоростью на 4 км/ч больше прежней. По дороге он сделал остановку на 4 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч.
Ответ: 1) 11 км/ч, 2) 7 км/ч.
Проверка

Прототип задания B12 (№ 26587)
- Решите задачу
Моторная лодка в 10:00 вышла из пункта А в пункт В, расположенный в 30 км от А. Пробыв в пункте В 2 часа 30 минут, лодка отправилась назад и вернулась в пункт А в 18:00. Определите (в км/час) собственную скорость лодки, если известно, что скорость течения реки 1 км/ч.
Обозначим за х км/ч– собственную скорость лодки. (х-1) км/ч – скорость против течения; (х=1) км/ч – скорость по течению. Составим уравнение:
30/(х+1)+30/(х-1)+2.5=8
Его корни:
-1/11 и 11.
Ответ: 11 км/ч.
Решение

Задания для самостоятельного решения
1) Байдарка в 10:00 вышла из пункта А в пункт В, расположенный в 15 км от А. Пробыв в пункте В 1 час 20 минут, байдарка отправилась назад и вернулась в пункт А в 16:00. Определите (в км/час) собственную скорость байдарки, если известно, что скорость течения реки 2 км/ч.
2) Лодка в 9:00 вышла из пункта А в пункт В, расположенный в 15 км от А. Пробыв в пункте В 2 часа, лодка отправилась назад и вернулась в пункт А в 19:00. Определите (в км/час) собственную скорость лодки, если известно, что скорость течения реки 1 км/ч.
Ответ:
1)7 км/ч;
2) 4 км/ч
Проверка
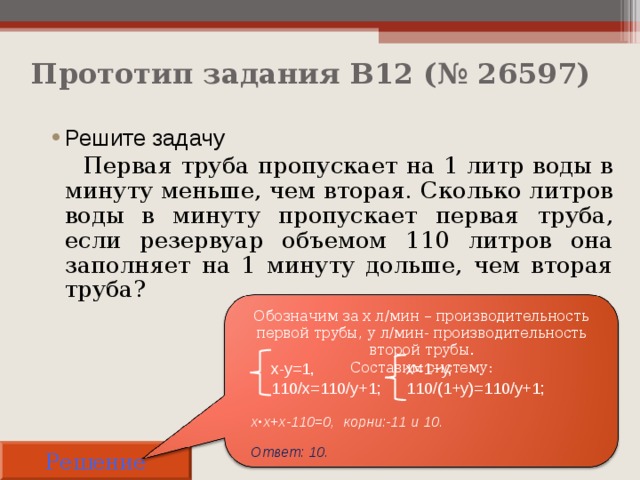
Прототип задания B12 (№ 26597)
- Решите задачу
Первая труба пропускает на 1 литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 110 литров она заполняет на 1 минуту дольше, чем вторая труба?
Обозначим за х л/мин – производительность первой трубы, у л/мин- производительность второй трубы.
Составим систему:
х-у=1,
110/х=110/у+1;
х=1+у,
110/(1+у)=110/у+1;
х•х+х-110=0, корни:-11 и 10.
Ответ: 10.
Решение

Задания для самостоятельного решения
1)Первая труба пропускает на 4 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 192 литра она заполняет на 4 минуты дольше, чем вторая труба?
2)Первая труба пропускает на 4 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 165 литров она заполняет на 4 минуты дольше, чем вторая труба?
Ответ:
1) 12 литров
2)11 литров
Проверка

Прототип задания B12 (№ 26592)
- Решите задачу
Заказ на 110 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 1 деталь больше?
Обозначим за х – производительность 1 рабочего,
за у – производительность второго рабочего.
Составим систему:
х=1+у,
110/х-1=110/у;
х=1+у,
110/(1+у)-1=110/у;
х•х+х-110=0, корни:-11 и 10.
Ответ: 10.
Решение

Задания для самостоятельного решения
1)Заказ на 180 деталей первый рабочий выполняет на 3 часа быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 3 детали больше?
2)Заказ на 182 детали первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 1 деталь больше?
Ответ:
1)12 деталей
2)13 деталей
Проверка

Список рекомендуемой литературы и адреса сайтов в сети Интернет
- Самое полное издание типовых вариантов реальных заданий ЕГЭ: 2010: Математика / авт.-сост. И.Р.Высоцкий, Д.Д.Гущин, П.И.Захаров и др.; под ред. А.Л.Семенова, И.В.Ященко. – М.:АСТ:Астрель, 2010. – 93, (3)с. – (Федеральный институт педагогических измерений)
- Математика: тематическое планирование уроков подготовки к экзамену / Белошистая.В. А. –М: Издательство «Экзамен», 2007. – 478 (2) с. (Серия «ЕГЭ 2007. Поурочное планирование»)
- Математика: самостоятельная подготовка к ЕГЭ / Л.Д. Лаппо, М.А. Попов. – 3-е изд., перераб. И дополн. - М.: Издательство «Экзамен», 2009. – 381, (3) с. (Серия «ЕГЭ. Интенсив»)
- Математика. Решение задач группы В / Ю.А.Глазков, И.А.Варшавский, М.Я. Гаиашвилли. – М.: Издательство «Экзамен», 2009. – 382 (2) с. (Серия «ЕГЭ. 100 баллов»)
- Математика: тренировочные тематические задания повышенной сложности с ответами для подготовки к ЕГЭ и к другим формам выпускного и вступительного экзаменов /сост Г.И.Ковалева, Т.И.Бузулина, О.Л.Безрукова, Ю.А. Розка. _ Волгоград: Учитель, 20089, - 494 с.
- Шабунин М.И. и др. Алгебра и начала анализа: Дидактические материалы для 10-11 кл. – 3-е изд. – М.: Мнемозина, 2000. – 251 с.: ил.

Адреса сайтов в сети Интернет
- www.fipi.ru – Федеральный институт педагогических измерений (ФИПИ). Особенно обратите внимание на раздел «Открытый сегмент ФБТЗ» – это система для подготовки к ЕГЭ - в режиме on-line. Вы можете отвечать на вопросы банка заданий ЕГЭ по различным предметам, а так же по выбранной теме.
- http://mathege.ru - Открытый банк задач ЕГЭ по математике . Главная задача открытого банка заданий ЕГЭ по математике — дать представление о том, какие задания будут в вариантах Единого государственного экзамена по математике в 2010 году, и помочь выпускникам сориентироваться при подготовке к экзамену. Здесь же можно найти все пробные ЕГЭ по математике, которые уже прошли.
- http://egetrener.ru/ - математика: видеоуроки, решение задач ЕГЭ.
- http://ege-trener.ru/ - очень увлекательная и эффективная подготовка к ЕГЭ по математике. Зарегистрируйтесь и попытайтесь попасть в 30-ку лучших!
- uztest.ru — бесплатные материалы для подготовки к ЕГЭ (и не только к ЕГЭ) по математике: интерактивные тематические тренажеры, возможность записи на бесплатные on-line курсы по подготовке к ЕГЭ.
- www.ege.edu.ru – официальный информационный портал единого государственного экзамена.
- On-line видеолекции "Консультации по ЕГЭ" по всем предметам.
- Ролики категории ЕГЭ. Лекции по математике
- http://www.alexlarin.narod.ru/ege.html - материалы для подготовки к ЕГЭ по математике (сайт Ларина Александра Александровича).
- http://www.diary.ru/~eek/ - сообщество, оказывающее помощь в решении задач по математике, здесь же можно скачать много полезных книг по математике, в том числе для подготовки к ЕГЭ.
- http://4ege.ru/ - ЕГЭ портал, всё последнее к ЕГЭ. Вся информация о егэ. ЕГЭ 2010.





