Ответы к олимпиаде по математике 10 класс
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| А |
|
|
|
|
|
|
|
|
|
|
| Б |
|
|
|
|
|
|
|
|
|
|
| В |
|
|
|
|
|
|
|
|
|
|
| Г |
|
|
|
|
|
|
|
|
|
|
Решения к олимпиаде по математике 10 класс
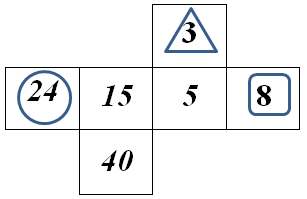
1. В каком году родился человек, если в 2017 году ему исполнилось количество лет, равное сумме цифр года рождения?
А) 1990 В) 1994
Б) 1992 Г) 1996
Ответ: В
Решение: Очевидно, что год рождения является четырехзначным числом, а сумма цифр четырехзначного числа не может превысить 36. Поэтому год рождения человека может иметь вид: 19ху или 20ху. Исходя из вариантов ответов видим, что речь о человеке, рожденном в 20 веке. Можем составить уравнение:
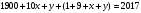 , или
, или
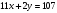
Из последнего уравнения следует, что 11х – нечетное число, значит х – нечетное число и, очевидно, 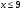 . Так как
. Так как 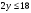 , то
, то 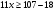 ,
, 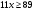 ,
, 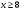 . Значит, х = 9. Тогда у = 4. Получаем год 1994.
. Значит, х = 9. Тогда у = 4. Получаем год 1994.
Решить можно было и обычной проверкой подходящих ответов.
2. Дан треугольник АВС. Точки M, N и K – середины сторон. Найдите площадь ромба АMNK, если площадь треугольника ABC равна 12.
А) 24 В) 6
Б) 12 Г) 4
Ответ: В
Решение: Меньший треугольник разбивает больший на 4 одинаковых части, ромб содержит 2 части, значит, его площадь в 2 раза меньше площади большого треугольника и равна 12:2=6.
3. Найдите зависимость между числами и вставьте пропущенное число: 1, 8, 22, 43, ?, 106.
А) 64 В) 71
Б) 70 Г) 78
Ответ: В
Решение: Заметим закономерность:
8=1+7, 22=8+14, 43=22+21, 43+28=71, 106=71+35.
4. Буквами М, А, Ш, И, Е, Д, В, Ь зашифрованы некоторые цифры, причем разные буквы обозначают разные цифры. Известно, что М+А+Ш+А+И+М+Е+Д+В+Е+Д+Ь= 34. Число МАША делится на 5, а число МЕДВЕДЬ – на 125. Какую цифру обозначает буква М?
А) 2 В) 4
Б) 3 Г) 6
Ответ: Б
Решение: Поскольку МАША и МЕДВЕДЬ делятся на 5, то либо А = 5 и Ь = 0, либо А = 0, Ь = 5. Далее, МЕДВЕДЬ делится на 125, поэтому ЕДЬ является числом, кратным 125, причем все цифры должным быть различны. Это могут быть числа 125, 250, 375, 625, 750, 875. Так как в ЕДЬ нет буквы А, то это число не должно содержать одновременно цифры 0 и 5. Остаются числа 125, 375, 625 и 875.
По условию М+А+Ш+А+И+М+Е+Д+В+Е+Д+Ь = 34,
т.е. 2(А+М+Е+Д)+Ш+И+В+Ь = 34. (*)
Оценим наименьшее возможное значение левой части последнего равенства. Левая часть будет минимальна, если среди цифр, обозначенных буквами А, М, Е, Д будут цифры 0, 1, 2, 3, среди цифр, обозначенных буквами Ш, И, В, Ь будут цифры 4, 5, 6, 7.
Тогда 2(А+М+Е+Д)+Ш+И+В+Ь = 2(0+1+2+3)+4+5+6+7=34.
Это означает что 34 – это наименьшее значение выражения, стоящего в левой части (*). Следовательно, А=0, Ь=5. Так как цифры Е и Д не могут превышать 3, то ЕДЬ = 125. Значит, Е=1, Д=2, тогда М=3
5. На отрезке АВ отмечены его концы – точки А и В, а также еще 3 точки, отличные от А и В (см. рисунок). Далее на отрезке АВ, как на диаметре, строится полуокружность. На полуокружности отмечаются еще 5 точек, отличных от А и В. (Всего отмечено 10 точек). Надя, Ваня и Вася играют в такую игру. Они по очереди рисуют треугольники с вершинами в отмеченных точках. При этом каждый новый треугольник не должен полностью совпадать ни с одним из уже нарисованных, хотя и может иметь с ними отдельные общие вершины и стороны. Первой ходит Надя, вторым – Ваня, третьим – Вася. Выигрывает тот, после чьего хода, следующий за ним игрок не сможет нарисовать треугольник. Кто выиграет при правильной игре?
А) Надя В) Вася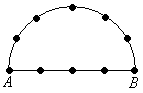
Б) Ваня Г) Ничья
Ответ: Б
Решение: Подсчитаем наибольшее возможное количество построенных треугольников. Первую вершину треугольника можно выбрать 10 способами, вторую – 9, третью – 8. Итого три вершины можно выбрать 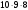 способами. Необходимо учесть, что выбранные три вершины (например, А, В, С) могут быть выбраны в разном порядке: АВС, АСВ, ВАС, ВСА, САВ, СВА (всего 6 вариантов). Поэтому количество различных троек точек будет равно
способами. Необходимо учесть, что выбранные три вершины (например, А, В, С) могут быть выбраны в разном порядке: АВС, АСВ, ВАС, ВСА, САВ, СВА (всего 6 вариантов). Поэтому количество различных троек точек будет равно 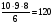 . (Знакомые с формулами комбинаторики тот же результат могут просто получить по формуле
. (Знакомые с формулами комбинаторики тот же результат могут просто получить по формуле 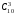 ). Заметим, что если три точки лежат на одной прямой, то они не образуют треугольник. В нашем случае это будут три точки, лежащие на отрезке АВ. Несложно подсчитать, что из 5 точек 3 точки можно выбрать 10 способами (
). Заметим, что если три точки лежат на одной прямой, то они не образуют треугольник. В нашем случае это будут три точки, лежащие на отрезке АВ. Несложно подсчитать, что из 5 точек 3 точки можно выбрать 10 способами (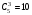 ). Таким образом, всего может получиться 120 – 10 = 110 различных треугольников. Поскольку число 110 при делении на 3 дает остаток 2, то последний 110-й треугольник нарисует игрок, делающий ход вторым, т. е. Ваня.
). Таким образом, всего может получиться 120 – 10 = 110 различных треугольников. Поскольку число 110 при делении на 3 дает остаток 2, то последний 110-й треугольник нарисует игрок, делающий ход вторым, т. е. Ваня.
6. Мама, папа, сын и малютка-дочка отправились навестить бабушку. Когда они подошли к ветхому мосту, уже стемнело. Мама переходит мост за 7 минут, Папа за 2 минуты, дочка – за 9, сын – за 1. Мост настолько плох, что идти без фонарика никак нельзя, причем мост выдерживает не больше двоих путешественников, и если идут двое, то идут со скоростью самого медленного в паре. За какое наименьшее количество времени семья сможет попасть на тот берег?
А) 16 В) 18
Б) 17 Г) 20
Ответ: А
Решение:
Если двое идут со скоростью самого медленного, то нужно двух самых медленных отправить вместе, и чтобы они не возвращались. Для этого на том берегу их должны ждать (фонарик забрать), поэтому первыми идут папа и сын – 2 минуты, возвращается папа с фонариком – 1 минута, мама и дочка идут 9 минут, возвращается сын 2 минуты, и он с папой идет через мост – 2 минуты. Итого 2+1+9+2+2=16 минут.
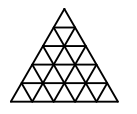
7. Осматривая старинный замок, путешественник заметил, что он треугольной формы, и при этом разбит на 49 маленьких комнат, такой же треугольной формы (как на рисунке). Во всех стенах между комнатами есть двери. Путешественник, гуляя по замку, планирует не посещать ни одной комнаты дважды. Найдите наибольшее число комнат, которое ему удастся посетить.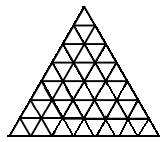
А) 42 В) 44
Б) 43 Г) 45
Ответ: Б
Решение: Раскрасим комнаты зала в два цвета, в «шахматном» порядке, чтобы 2 комнаты с общей дверью были разного цвета. Тогда проходя по комнатам, путешественник из белой идет в черную, из черной – в белую. Значит, количество пройденных комнат по цвету будет или одинаковым (например, начали с белой комнаты, закончили черной), или отличаться на 1 (если начать и закончить белой комнатой, или наоборот, черной). 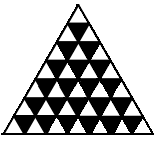
Подсчитаем комнаты черного цвета: 1+2+3+4+5+6=21. Тогда белых пройдет путешественник не более 22, и 22+21=43 – наибольшее количество пройденных комнат.
8. В одной отборочной группе к чемпионату мира по футболу среди юношей играли команды России, Беларуси, Польши, Эстонии и Болгарии. Каждая команда сыграла со всеми остальными по два матча: на своем поле и в гостях. За победу команде начислялось 3 очка, за ничью начислялось 1 очко, за поражение – 0 очков. По окончании турнира команды набрали следующее количество очков:
| Место | Страна | Количество очков |
| 1 | Россия | 16 |
| 2 | Беларусь | 13 |
| 3 | Болгария | 10 |
| 4 | Польша | 9 |
| 5 | Эстония | 3 |
Сколько матчей турнира закончилось вничью?
А) 7 В) 9
Б) 8 Г) 10
Ответ: В
Решение: Подсчитаем, сколько всего матчей было сыграно на турнире. Каждая команда сыграла по 8 матчей. Всего матчей было 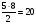 (делим на 2, поскольку каждый матч подсчитывается дважды: если играли команды А и Б, то эта игра идет в зачет каждой из этих команд). В каждом матче разыгрывалось 3 очка (если игра завершилась победой одной из команд) или 2 очка (если игра завершилась вничью). Если бы все игры закончились победой одной из команд, то общее количество очков, набранных командами, было бы равно
(делим на 2, поскольку каждый матч подсчитывается дважды: если играли команды А и Б, то эта игра идет в зачет каждой из этих команд). В каждом матче разыгрывалось 3 очка (если игра завершилась победой одной из команд) или 2 очка (если игра завершилась вничью). Если бы все игры закончились победой одной из команд, то общее количество очков, набранных командами, было бы равно 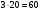 . Каждая игра вничью вычитает из этого числа единицу. Все команды набрали вместе 16+13+10+9+3=51 очко. Тогда вничью закончились 60 – 51 = 9 матчей.
. Каждая игра вничью вычитает из этого числа единицу. Все команды набрали вместе 16+13+10+9+3=51 очко. Тогда вничью закончились 60 – 51 = 9 матчей.
9. Дан треугольник. На одной из его сторон отмечено 5 различных точек, не совпадающих с вершинами, на второй стороне отмечено 8 различных точек, не совпадающих с вершинами, на третьей стороне – 12 различных точек, не совпадающих с вершинами треугольника. Сколько существует различных треугольников с вершинами в отмеченных точках?
А) 2014 В) 2016
Б) 2015 Г) 2017
Ответ: А
Решение: Всего на контуре исходного треугольника отмечены 5+8+12=25 точек. Первую вершину построенного треугольника можно выбрать 25 способами, вторую – 24, третью- 23. Итого три вершины можно выбрать 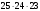 способами. Необходимо учесть, что выбранные три вершины (например, А, В, С) могут быть выбраны в разном порядке: АВС, АСВ, ВАС, ВСА, САВ, СВА (всего 6 вариантов). Поэтому количество различных троек точек будет равно
способами. Необходимо учесть, что выбранные три вершины (например, А, В, С) могут быть выбраны в разном порядке: АВС, АСВ, ВАС, ВСА, САВ, СВА (всего 6 вариантов). Поэтому количество различных троек точек будет равно 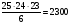 . (Знакомые с формулами комбинаторики тот же результат могут просто получить по формуле
. (Знакомые с формулами комбинаторики тот же результат могут просто получить по формуле 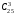 ). Заметим, что если три точки лежат на одной прямой, то они не образуют треугольник. Если три точки выбраны на стороне с 5-ю точками, то таких троек будет
). Заметим, что если три точки лежат на одной прямой, то они не образуют треугольник. Если три точки выбраны на стороне с 5-ю точками, то таких троек будет 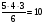 (
(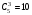 ).Если три точки выбраны на стороне с 8-ю точками, то таких троек будет
).Если три точки выбраны на стороне с 8-ю точками, то таких троек будет 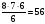 (
(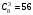 ). Если три точки выбраны на стороне с 12-ю точками, то таких троек будет
). Если три точки выбраны на стороне с 12-ю точками, то таких троек будет 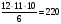 (
(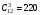 ).
).
Таким образом, получится 2300–10–56–220 = 2014 различных треугольников.
10. Маша и Саша – брат и сестра. Маше вдвое больше лет, чем было Саше тогда, когда Маше было столько, сколько Саше теперь. Когда Саше будет столько лет, сколько Маше сейчас, сумма их возрастов будет равна 63 годам. Сколько лет каждому?
А) Маше 33, Саше 30 В) Маше 28, Саше 21
Б) Маше 18, Саше 17 Г) Маше 25, Саше 10
Ответ: В
Решение:
Составим и заполним таблицу:
|
| Тогда | Теперь | Будет |
| Маше | х | 2у | х + у |
| Саше | у | х | 2у |
Пусть Маше было х лет, Саше у лет. Заполним таблицу по условию задачи. Разность возрастов брата и сестры равна х – у = 2у – х (на столько лет Маша старше Саши). Когда Саше будет 2у лет, разность возрастов останется той же, значит Маше будет 2у + х – у = х + у лет. Мы знаем, что сумма возрастов брата и сестры будет равна 63, получаем второе уравнение: х + у + 2у = 63.
Решим систему уравнений:
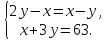
Решив систему, получаем, х = 21, у = 14. Значит Маше сейчас 28 лет, Саше 21 год.
7
![]()


 ешение:
ешение:  ) 4 Г) 3
) 4 Г) 3
 . Две маленькие кошки сидели на окошке.
. Две маленькие кошки сидели на окошке. 

 . Три оленя везли сани с Дедом Морозом. Каждый олень бежал 1 час. Сколько времени везли олени сани с Дедом Морозом?
. Три оленя везли сани с Дедом Морозом. Каждый олень бежал 1 час. Сколько времени везли олени сани с Дедом Морозом? 


 ыбери один из предложенных вариантов.
ыбери один из предложенных вариантов.
 ешение:
ешение:
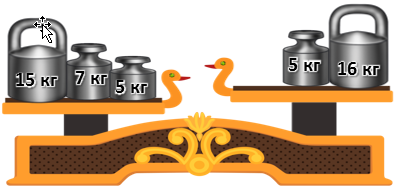 . Какую дыню надо положить на правую чашу весов, чтобы весы были в равновесии?
. Какую дыню надо положить на правую чашу весов, чтобы весы были в равновесии?

 ешение:
ешение:
 ешение:
ешение: 
 ешение:
ешение:  0 км/ч, и через каждые 3 ч делал остановку на полчаса для того, чтобы отдохнули его олени. Сколько времени заняла вся дорога от Великого Устюга до Вологды?
0 км/ч, и через каждые 3 ч делал остановку на полчаса для того, чтобы отдохнули его олени. Сколько времени заняла вся дорога от Великого Устюга до Вологды? 
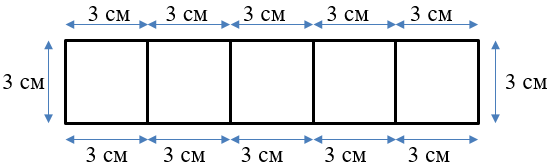
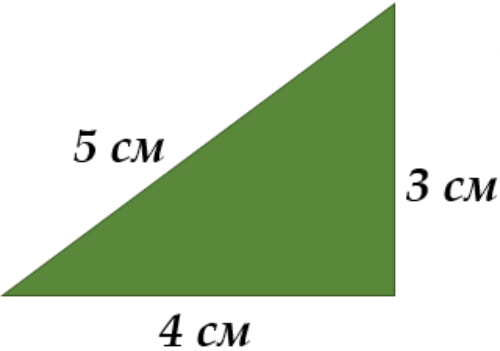 . Посмотри на треугольник. Из восьми таких треугольников составили прямоугольник. Чему равна его площадь?
. Посмотри на треугольник. Из восьми таких треугольников составили прямоугольник. Чему равна его площадь?


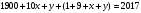 , или
, или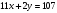
 . Так как
. Так как  , то
, то 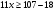 ,
, 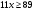 ,
, 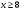 . Значит, х = 9. Тогда у = 4. Получаем год 1994.
. Значит, х = 9. Тогда у = 4. Получаем год 1994.
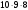 способами. Необходимо учесть, что выбранные три вершины (например, А, В, С) могут быть выбраны в разном порядке: АВС, АСВ, ВАС, ВСА, САВ, СВА (всего 6 вариантов). Поэтому количество различных троек точек будет равно
способами. Необходимо учесть, что выбранные три вершины (например, А, В, С) могут быть выбраны в разном порядке: АВС, АСВ, ВАС, ВСА, САВ, СВА (всего 6 вариантов). Поэтому количество различных троек точек будет равно 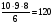 . (Знакомые с формулами комбинаторики тот же результат могут просто получить по формуле
. (Знакомые с формулами комбинаторики тот же результат могут просто получить по формуле 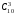 ). Заметим, что если три точки лежат на одной прямой, то они не образуют треугольник. В нашем случае это будут три точки, лежащие на отрезке АВ. Несложно подсчитать, что из 5 точек 3 точки можно выбрать 10 способами (
). Заметим, что если три точки лежат на одной прямой, то они не образуют треугольник. В нашем случае это будут три точки, лежащие на отрезке АВ. Несложно подсчитать, что из 5 точек 3 точки можно выбрать 10 способами (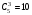 ). Таким образом, всего может получиться 120 – 10 = 110 различных треугольников. Поскольку число 110 при делении на 3 дает остаток 2, то последний 110-й треугольник нарисует игрок, делающий ход вторым, т. е. Ваня.
). Таким образом, всего может получиться 120 – 10 = 110 различных треугольников. Поскольку число 110 при делении на 3 дает остаток 2, то последний 110-й треугольник нарисует игрок, делающий ход вторым, т. е. Ваня.

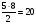 (делим на 2, поскольку каждый матч подсчитывается дважды: если играли команды А и Б, то эта игра идет в зачет каждой из этих команд). В каждом матче разыгрывалось 3 очка (если игра завершилась победой одной из команд) или 2 очка (если игра завершилась вничью). Если бы все игры закончились победой одной из команд, то общее количество очков, набранных командами, было бы равно
(делим на 2, поскольку каждый матч подсчитывается дважды: если играли команды А и Б, то эта игра идет в зачет каждой из этих команд). В каждом матче разыгрывалось 3 очка (если игра завершилась победой одной из команд) или 2 очка (если игра завершилась вничью). Если бы все игры закончились победой одной из команд, то общее количество очков, набранных командами, было бы равно 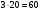 . Каждая игра вничью вычитает из этого числа единицу. Все команды набрали вместе 16+13+10+9+3=51 очко. Тогда вничью закончились 60 – 51 = 9 матчей.
. Каждая игра вничью вычитает из этого числа единицу. Все команды набрали вместе 16+13+10+9+3=51 очко. Тогда вничью закончились 60 – 51 = 9 матчей.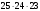 способами. Необходимо учесть, что выбранные три вершины (например, А, В, С) могут быть выбраны в разном порядке: АВС, АСВ, ВАС, ВСА, САВ, СВА (всего 6 вариантов). Поэтому количество различных троек точек будет равно
способами. Необходимо учесть, что выбранные три вершины (например, А, В, С) могут быть выбраны в разном порядке: АВС, АСВ, ВАС, ВСА, САВ, СВА (всего 6 вариантов). Поэтому количество различных троек точек будет равно 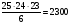 . (Знакомые с формулами комбинаторики тот же результат могут просто получить по формуле
. (Знакомые с формулами комбинаторики тот же результат могут просто получить по формуле 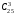 ). Заметим, что если три точки лежат на одной прямой, то они не образуют треугольник. Если три точки выбраны на стороне с 5-ю точками, то таких троек будет
). Заметим, что если три точки лежат на одной прямой, то они не образуют треугольник. Если три точки выбраны на стороне с 5-ю точками, то таких троек будет 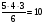 (
(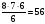 (
(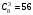 ). Если три точки выбраны на стороне с 12-ю точками, то таких троек будет
). Если три точки выбраны на стороне с 12-ю точками, то таких троек будет 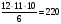 (
(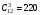 ).
). 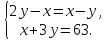
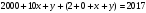 , или
, или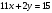 , х=1, у = 2. Получаем год 2012.
, х=1, у = 2. Получаем год 2012.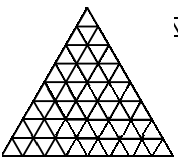
 ). Окружность, проходящая через точку В и касающаяся стороны АС в точке М, пересекает стороны АВ и ВС в точках К и L соответственно. Отрезки ВМ и КL пересекаются в точке Р, при этом ВР:РМ=5:1. Найти площадь треугольника АВС, если площадь треугольника КВL равна 100 кв.ед.
). Окружность, проходящая через точку В и касающаяся стороны АС в точке М, пересекает стороны АВ и ВС в точках К и L соответственно. Отрезки ВМ и КL пересекаются в точке Р, при этом ВР:РМ=5:1. Найти площадь треугольника АВС, если площадь треугольника КВL равна 100 кв.ед. 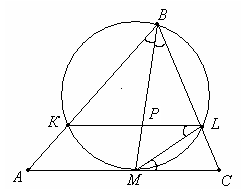
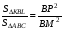 ,
, 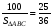 , SАВС= 144.
, SАВС= 144. (делим на 2, поскольку каждый матч подсчитывается дважды: если играли команды А и Б, то эта игра идет в зачет каждой из этих команд). В каждом матче разыгрывалось 3 очка (если игра завершилась победой одной из команд) или 2 очка (если игра завершилась вничью). Если бы все игры закончились победой одной из команд, то общее количество очков, набранных командами, было бы равно
(делим на 2, поскольку каждый матч подсчитывается дважды: если играли команды А и Б, то эта игра идет в зачет каждой из этих команд). В каждом матче разыгрывалось 3 очка (если игра завершилась победой одной из команд) или 2 очка (если игра завершилась вничью). Если бы все игры закончились победой одной из команд, то общее количество очков, набранных командами, было бы равно 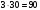 . Каждая игра вничью вычитает из этого числа единицу. Все команды набрали вместе 22+21+14+9+7+6=79 очков.
. Каждая игра вничью вычитает из этого числа единицу. Все команды набрали вместе 22+21+14+9+7+6=79 очков. 
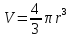
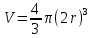 , объем косточки
, объем косточки 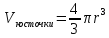 , объем мякоти вишенки – это разность объема всей вишни и косточки. Тогда отношение объема мякоти к объему косточки равно
, объем мякоти вишенки – это разность объема всей вишни и косточки. Тогда отношение объема мякоти к объему косточки равно 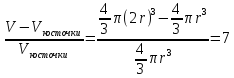
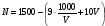 . Минимально возможное значение величины
. Минимально возможное значение величины 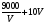 можно определить при помощи производной, либо используя неравенство Коши:
можно определить при помощи производной, либо используя неравенство Коши: 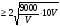 =
=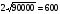 (монет). Заработок хозяина в этом случае составит
(монет). Заработок хозяина в этом случае составит 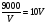 , откуда V= 30 (км/ч).
, откуда V= 30 (км/ч).
 ;
; 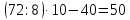 .
. 
 Б)
Б)  В)
В)  Г)
Г) 
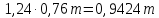 . Таким образом, видно, что конфеты «Кузнечик» самые дорогие.
. Таким образом, видно, что конфеты «Кузнечик» самые дорогие.

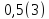 Б) -12,014114111441111… В)
Б) -12,014114111441111… В) 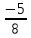 Г) 13578
Г) 13578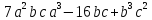 Б)
Б) 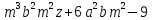
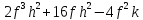 Г)
Г) 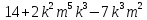
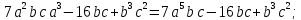 — многочлен 7 степени;
— многочлен 7 степени; 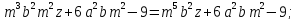 — многочлен 8 степени;
— многочлен 8 степени; 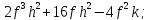 — многочлен 5 степени;
— многочлен 5 степени; 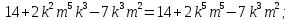 — многочлен 10 степени.
— многочлен 10 степени.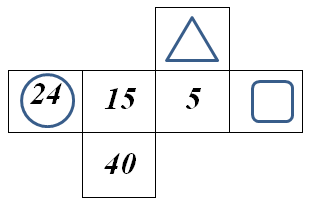
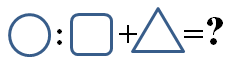
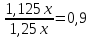 , значит исходное количество уменьшили на 10%.
, значит исходное количество уменьшили на 10%.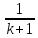
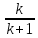 стакана яблочного сока.
стакана яблочного сока.