Краевое государственное бюджетное профессиональное образовательное учреждение «Каменский медицинский колледж»
ТЕХНОКАРТА ТЕОРЕТИЧЕСКОГО ЗАНЯТИЯ №6
«ПРАВИЛЬНЫЕ МНОГОГРАННИКИ»
Разработано преподавателем
математики и физики Бутаковой Н.Г.
Камень-на-Оби, 2019г.
ТЕХНОКАРТА ТЕОРЕТИЧЕСКОГО ЗАНЯТИЯ №6
Дисциплина Математика: алгебра и начала анализа; геометрия
Специальность 34.02.01 Сестринское дело
(код наименование)
Курс 1 Семестр 2
Тема: Представление о правильных многогранниках
Количество часов 2
Цели :
Образовательные:
повторение общих сведений о многогранниках;
изучение пяти видов правильных многогранников, истории их открытия, связи с окружающей действительностью;
закрепление знаний в процессе решения задач, выполнения индивидуальных и групповых заданий.
Развивающие:
развитие образного мышления студентов;
развитие навыков анализирования, сравнения, обобщения и систематизации информации;
развитие навыков самостоятельной работы студентов и навыков работы в группе.
Воспитательные:
стимулирование познавательной активности студентов;
воспитанник культуры конструктивного мышления, культуры владения математическим языком;
воспитание личностных качеств, обеспечивающих продуктивную исполнительскую и творческую деятельность.
Студент должен
знать:
Определять понятия многогранника и правильного многогранника; называть и перечислять основные элементы и свойства правильных многогранников;
Обеспечение занятия:
1.Оборудование:
Конспект лекции, раздаточный материал, учебник (приборы, инструменты, посуда, расходный материал и т.п.)
2.Технические средства обучения:
Компьютер, проектор
(аудио- и визуальные средства, компьютерная техника, мультимедийная установка, т.п.)
3.Методическое обеспечение:
технологическаяе карта
(Методические рекомендации/ указания/разработки для студентов; контролирующие материалы, раздаточные материалы и т.п.)
Структура и содержание занятия
| № | Этап занятия | Время | Содержание этапа | Деятельность | |
| Преподавателя | Студента | ||||
| 1 | Организационный | 2-3 | Оценка готовности аудитории и студентов
| Приветствие, преподаватель настраивает студентов на плодотворную работу, концентрирует их внимание. | Приветствие преподавателя. |
| 2 | Сообщение темы и цели занятия | 2-3 | Характеристика порядка проведения лекции | Сообщает тему и цель занятия. Предлагает поучаствовать в игре «До – после» | Слушают, записывают тему. Заполняют столбик ответов на вопросы «До» |
| 3 | Основной этап. Актуализации знаний. Опрос.
|
5-7
|
Актуализация и мотивация деятельности студентов. Фронтальная беседа |
Преподаватель выясняет знания студентов относительно ключевых понятий темы. |
Слушают, смотрят. Отвечают на вопросы преподавателя. |
|
| Опрос.
| 5-7 | Работа в тетради по заданию на экране | Акцентирует внимание на наиболее важных аспектах. | Смотрят Читают Записывают ответы в тетрадь. Проверяют и самооценивают. |
| 4 | Изложение нового материала | 12-15 | Изложение плана лекции. | Преподаватель излагает новый материал. | Слушают, конспектируют. |
| 10-12 | Сообщения студентов по теме с демонстрацией модели многогранника | Регламентирует, консультирует | Докладчики излагают свою часть Остальные слушают, конспектируют материала заполняют сводную | ||
|
|
|
| таблицу на листочках. | ||
|
|
| 12-15 | Сообщение студентов по теме в сопровождении презентации | Регламентирует, консультирует | Докладчики излагают свою часть. Остальные слушают. |
| 5 | Закрепление | 10-12 | Решение задач | Организует работу студентов по решению задач, контролирует процесс и результат решения. | Решают задачи, записывают решение в тетрадях. |
| 6 | Этап контроля знаний | 10
| Решение кроссворда | Организует работу студентов по решению кроссворда, контролирует процесс и результат решения. | Отвечают на вопросы кроссворда. |
| 7 | Этап подведения итогов урока | 3-5
| Рефлексия | Завершает прием «До-После» | Заполняют столбик «После» в табличке, делают вывод. Определяют свое эмоциональное состояние на уроке. |
|
|
| 3 | Домашнее задание Выставление оценок | Задает домашнее задание, выставляет оценки, благодарит за работу. | Слушают задание. |
|
| Всего | 90 |
|
|
|
Ход занятия:
Организационный этап
Преподаватель: - приветствие, проверка готовности аудитории, отмечает кого нет.
Великий математик Гильберт сказал: «В огромном саду геометрии каждый найдет себе букет по вкусу». Слайд №1
Так вот сегодня мы познакомимся, наверное, с самыми красивыми цветами этого сада.
Этап активизации студентов
Тема нашего занятия: «Правильные многогранники».
Цель урока – изучение пяти видов правильных многогранников и истории их открытия. Слайд №2
Запишите тему в тетрадь.
Но прежде чем начать изучать новый материал, предлагаю провести маленький эксперимент: вы ответите на несколько вопросов до изучения темы и после. В конце занятия мы сделаем выводы.
Заполните столбик «До» в таблице вопросов, так как вы считаете правильным.
Используется раздаточный материал (Приложение 1)
Этап актуализации базовых знаний
Начнём наше занятие с традиционного повторения. Внимание на экран. Первое задание
Фронтальный опрос: ответить на вопросы по рисункам, спроектированным на экран.
Слайд № 3.
Дайте все возможные названия этого многогранника
Дать характеристику многогранника(Что общего и чем отличаются).
Слайд № 4..
Дать характеристику многогранника.
Назовите грани, вершины и рёбра данного многогранника.
Слайд № 5.
Дать характеристику многогранника.
Можно ли в качестве высоты этой призмы принять боковое ребро?
Слайд № 6.
Дайте характеристику многогранника.
При каких условиях эта пирамида будет правильной?
В следующем задании я предлагаю вам проверить себя на знание формул по темам «Призма» и «Пирамида». Пропущенными могут быть как компоненты формулы, так и её название.
Работа в тетрадях: заполнить пропуски (задание спроектировано на экран), выполнить самопроверку (эталон ответов выведен на экран)
Слайд № 7.
Заполните пропуски
S=PоH -------------------------------------------------------------
----------- - площадь полной поверхности пирамиды
S=1/2Pоh - --------------------------------------------------------
S=Sб + 2Sо - ------------------------------------------------------
S=1/2(Pо + Ро)h - -------------------------------------
Слайд № 8.
Эталоны ответов
S = Pо H – площадь боковой поверхности призмы
S = Sб + So – площадь полной поверхности пирамиды
S = ½ Pо H – площадь боковой поверхности правильной пирамиды
S = Sб + 2 Sо – площадь полной поверхности призмы
S=1/2(Pо + Ро)h – площадь боковой поверхности правильной
усечённой пирамиды
Слайд № 9 Оцените свою работу по следующим критериям оценки
Оценка «5» - все задания выполнены верно
Оценка «4» - выполнено 4 задания
Оценка «3» - выполнено не менее 3 заданий
Оценка «2» - выполнено менее 3 заданий
Этап изложения нового материала
Вступительное слово преподавателя
Слайд № 10
Мы с вами уже изучили разные виды многогранников: тетраэдр, параллелепипед, пирамиды, призмы. Но ни одно геометрическое тело не обладает такой красотой, как правильные многогранники, с которыми мы познакомимся на сегодняшнем занятии.
«Правильных многогранников вызывающе мало, но весьма скромный по численности отряд сумел пробраться в самые глубины различных наук»
(Л.Кэрролл.)
Ввод понятия правильного многогранника. (Слайд № 11,12,13).
Нами уже использовались словосочетания “правильные призмы” и “правильные пирамиды”. Но оказывается, новая комбинация знакомых понятий образует совершенно новое с геометрической точки зрения понятие. Какие же выпуклые многогранники будем называть правильными? Послушайте внимательно определение.
Многогранник называется правильным, если все его грани – равные правильные многоугольники и в каждой вершине сходится одно и то же число граней
правильным многогранником называется такой выпуклый многогранник, все грани которого являются одинаковыми правильными многоугольниками и все двугранные углы попарно равны.
Запишите в тетрадь какие многогранники называются правильными, если:
он выпуклый
все его грани являются равными правильными многоугольниками
в каждой его вершине сходится одинаковое число граней
все его двугранные углы равны
Слайд № 14
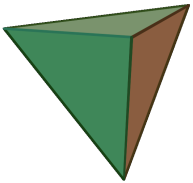
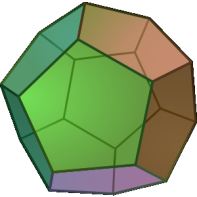
Существует всего пять правильных многогранников: тетраэдр, куб, октаэдр, додекаэдр, икосаэдр.
Название каждого многогранника происходит от греческого названия количества его граней и слова "грань":
(тетраэдр – составлен из 4 равносторонних треугольников;
куб (гексаэдр) – составлен из 6 квадратов;
октаэдр – составлен из 8 равносторонних треугольников;
додекаэдр – составлен из 12 равносторонних пятиугольников;
икосаэдр – составлен из 20 равносторонних треугольников.)
Как выглядят и какими свойствами они обладают, нам расскажут докладчики. В процессе их докладов мы заполним сравнительную таблицу.
(Приложение 3). Слайды 15-19
Выступления пяти докладчиков. Каждый рассказывает об одном из многогранников, демонстрирует склеенную им модель, заполняет соответствующую строчку в сравнительной таблице
| Многогран ник | Форма грани | Число рёбер Р | Число граней Г | Число вершин В | Число ребер, сходящихся в одной вершине | Сумма плоских углов при вер шине | Г+В - Р |
| Тетра эдр | Треугольник | 6 | 4 | 4 | 3 | 180° |
|
| Гекса эдр (Куб) | Ква драт | 12 | 6 | 8 | 3 | 270° |
|
| Окта эдр | Треугольник | 12 | 8 | 6 | 4 | 240° |
|
| Додекаэдр | Пятиугольник | 30 | 12 | 20 | 3 | 324° |
|
| Икоса эдр | Треугольник | 30 | 20 | 12 | 5 | 300° |
|
Проверим результаты заполнения таблицы (слайд №20).
Итак, подведем небольшой итог:
Названия этих многогранников пришли из Древней Греции, и в них указывается число граней:
«эдра» - грань
«тетра» - 4
«гекса» - 6
«окта» - 8
«икоса» - 20
«додека» - 12
Слайд № 21 Важно: Не существует правильного многогранника, гранями которого являются правильные шестиугольники, семиугольники и вообще
n-угольники при n≥ 6.
Слайд № 22
Характеристика Эйлера для правильных многогранников:
Число граней плюс число вершин минус число рёбер в любом многограннике равно 2.
Г + В - Р = 2
Слайд № 23 остается заполнить последнюю колонку в сравнительной таблице. Работают самостоятельно с последующей проверкой
Проверьте правильность заполнения.
Преподаватель:
Слайд №24 Правильные многогранники были открыты еще в Древней Греции. Более подробно об этом нам расскажет…...
Сообщение «История открытия правильных многогранников» в сопровождении презентации
Преподаватель:
Слайд №25 Правильные многогранники можно встретить везде, а где именно нам расскажет ….
Сообщение «Правильные многогранники вокруг нас» в сопровождении презентации
Этап закрепления знаний
Преподаватель: А теперь вам предлагается решить задачу.
(Слайд № 26). Задача . Определите количество граней, вершин и рёбер многогранника, изображённого на рисунке. Проверьте выполнимость формулы Эйлера для данного многогранника.

Решение : Г=12, В=10, Р=20, Г+В-Р=12+10-20=2
Студенты решают задачи сначала индивидуально, а затем записывают решение на доске. рассказывают для всех.
Преподаватель осуществляет выборочный контроль решения в тетрадях.
В случае затруднений возможны наводящие вопросы:
Из каких многогранников состоит эта фигура?
Сколько граней имеет многогранник?
Какой геометрической фигурой является каждая грань?
Какой геометрической фигурой является данное сечение?
Этап контроля знаний
Слайд № 27 Преподаватель: А теперь проверим, кто из вас лучше усвоил новый материал: кто быстрее разгадает кроссворд «Многогранники»? (Приложение 3)
Работа в группах по 4 человека. Проверка результата. Преподаватель подсчитывает, сколько слов правильно отгадала каждая группа. Объявляет победителей.
Этап подведения итогов урока
Рефлексия: А сейчас вернемся к нашему эксперименту. Возьмите таблички «До - после» и заполните последний столбик. Сделайте вывод.
Слайд № 28 Прежде чем закончить занятие, мне хочется рассказать вам притчу.
Шел мудрец, а навстречу ему три человека, которые везли под горячим
солнцем тележки с камнями для строительства храма. Мудрец остановил
первого и спросил: «Что ты делал целый день?» Человек ответил, что возил
проклятые камни. Второй ответил, что он добросовестно выполнял свою
работу. А третий улыбнулся и сказал радостно: «Я принимал участие в
строительстве храма!».
Давайте оценим каждый свою работу сегодня на занятии:
Кто работал как первый человек?
Кто работал добросовестно?
А кто «принимал участие в строительстве храма?»
Понравился ли вам занятие?
Слайд № 29 Домашнее задание будет сегодня творческим: склеить модели правильных многогранников на выбор (Приложение 4)
Слайд № 30 Спасибо за работу!
Приложения
Приложение 1
Приём «До-После»
| Вопрос | До | После |
| Какой многогранник называется правильным? |
|
|
| Может ли поверхность многогранника состоять только из шестиугольников? |
|
|
| Встречаются ли у живых организмов формы правильных многогранников? |
|
|
Вывод:
Я прав (не прав), так как ...
Приложение 2
Сравнительная характеристика правильных многогранников
| Многогран ник | Вид | Форма грани | Чис ло рё бер | Чис ло гра ней | Чис ло вер шин | Чис ло ребер, сходя щихся в 1 вер шине | Сума плоских углов при вер шине | Эйле рова харак тери стика |
| Тетра эдр |
|
|
|
|
|
|
|
|
| Гекса эдр (куб) |
|
|
|
|
|
|
|
|
| Окта эдр |
|
|
|
|
|
|
|
|
| Доде ка эдр |
|
|
|
|
|
|
|
|
| Икоса эдр |
|
|
|
|
|
|
|
|
Приложение 3
Кроссворд «Многогранники»
По горизонтали:
1. Высота боковой грани правильной пирамиды.(Апофема) 2. Правильный двадцатигранник.(икосаэдр) 3. Сторона грани многогранника.(ребро) 4. Древнегреческий философ, подробно описавший правильные многогранники.( Платон) 5. Призма, основанием которой служит параллелограмм.(Параллелепипед) 6. Правильный восьмигранник.(Октаэдр) 7. Многогранник, боковые грани которого представляют собой треугольники. (пирамида)
По вертикали:
8. Основание правильной четырёхугольной пирамиды.(квадрат) 9. Правильный двенадцатигранник. (Додекаэдр) 10. Взаимное расположение противолежащих граней куба.(параллельно) 11. Тело, поверхность которого состоит из конечного числа плоских многоугольников.(Многогранник) 12. Форма грани, дающая наибольшее число правильных многогранников. (треугольник) 13. Треугольная пирамида.(Тетраэдр) 14. Автор теоремы (формулы) В+Г=Р+2, показывающей зависимость между вершинами, гранями и рёбрами выпуклого многогранника.(Эйлер) 15. Плоские многоугольники, из которых состоит поверхность многогранника.(грань)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 11М |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Н |
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1А | П | О | Ф | Е | М | А |
|
|
|
|
|
|
|
|
|
|
|
| Г |
|
|
|
|
|
|
|
|
|
|
|
| 10П |
| 2И | К | О | С | А | Э | Д | Р |
|
| 8К |
| 9Д |
|
| А |
|
|
| Г |
|
|
|
|
|
|
| В |
| О |
|
| Р |
|
|
| 3Р | Е | Б | Р | О |
|
|
| А |
| Д |
|
| А |
|
|
| А |
|
|
|
|
|
|
| Д |
| Е |
| 4П | Л | А | 12Т | О | Н |
|
|
|
|
|
|
| Р |
| К |
|
| Л |
| Р |
| Н |
|
|
|
|
|
| 5П | А | Р | А | Л | Л | Е | Л | Е | П | И | п | е | д |
|
|
|
| Т |
| Э |
|
| Л |
| У |
| К |
|
|
|
|
|
|
|
|
| Д |
|
| Ь |
| Г |
|
|
|
|
| 15Г |
|
|
|
|
| Р |
|
| Н |
| 6О | К | 13Т | А | 14Э | Д | Р |
|
|
|
|
|
|
|
| О |
| Л |
| Э |
| Й |
| А |
|
|
|
|
|
|
|
|
|
| Ь |
| Т |
| Л |
| Н |
|
|
|
|
|
|
|
|
|
| Н |
| Р |
| Е |
| Ь |
|
|
|
|
| 7П | И | Р | А | М | И | Д | А |
| р |
|
|
|
|
|
|
|
|
|
|
|
| К |
| Э |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Д |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приложение 4