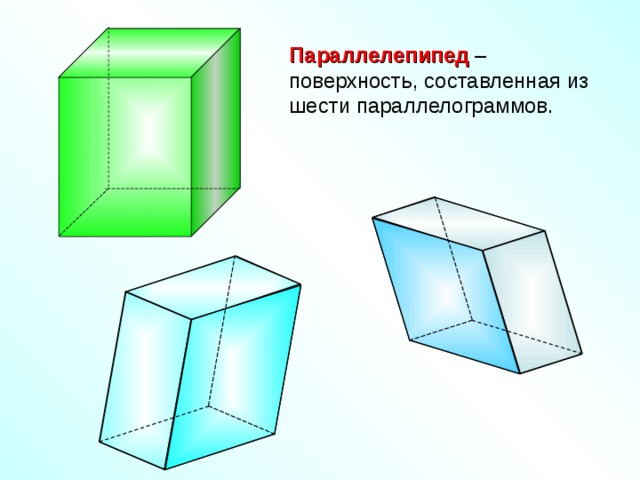
Параллелепипед – поверхность, составленная из шести параллелограммов.
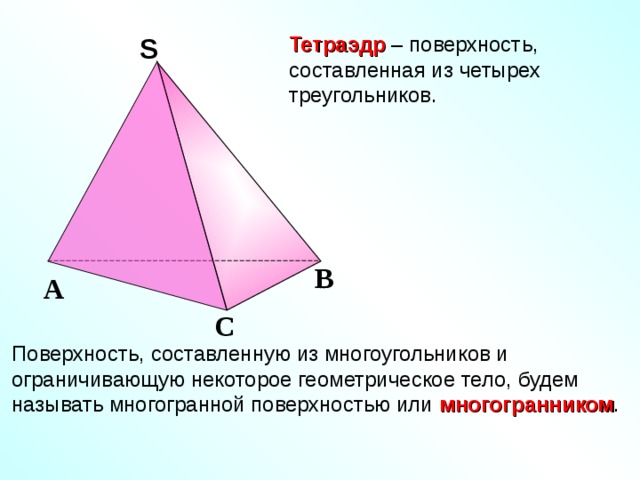
Тетраэдр – поверхность, составленная из четырех треугольников.
S
S
В
А
С
Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, будем называть многогранной поверхностью или многогранником .
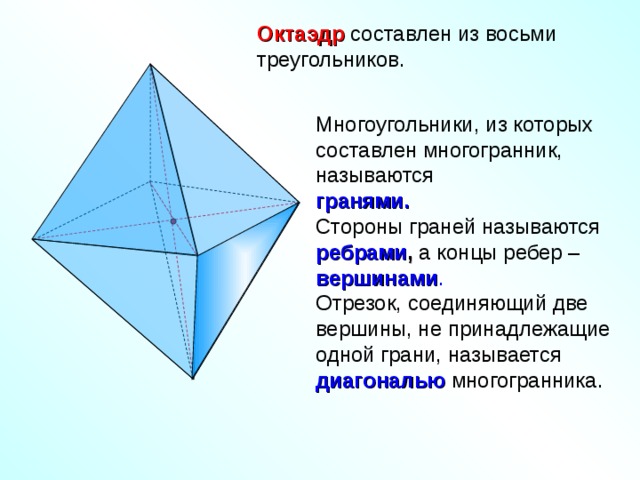
Октаэдр составлен из восьми треугольников.
Многоугольники, из которых составлен многогранник, называются
гранями.
Стороны граней называются ребрами , а концы ребер – вершинами .
Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника.
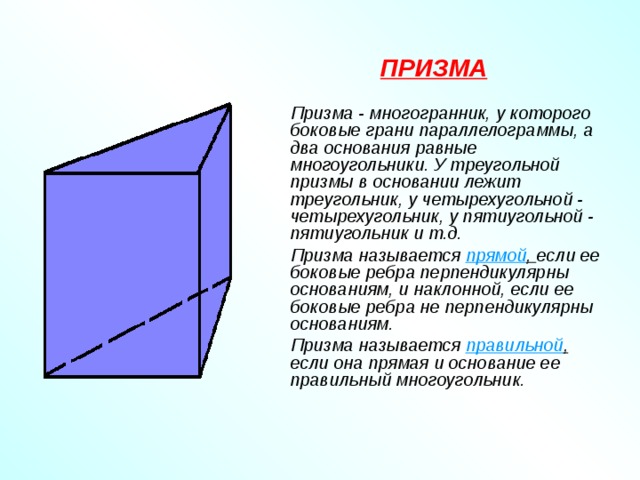
ПРИЗМА
Призма - многогранник, у которого боковые грани параллелограммы, а два основания равные многоугольники. У треугольной призмы в основании лежит треугольник, у четырехугольной - четырехугольник, у пятиугольной - пятиугольник и т.д.
Призма называется прямой , если ее боковые ребра перпендикулярны основаниям, и наклонной, если ее боковые ребра не перпендикулярны основаниям.
Призма называется правильной , если она прямая и основание ее правильный многоугольник.

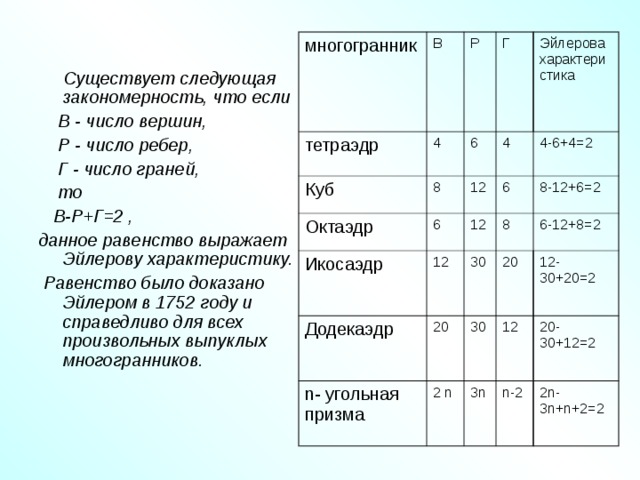
многогранник
В
тетраэдр
Р
Куб
4
Октаэдр
8
6
Г
4
Эйлерова характеристика
12
Икосаэдр
6
Додекаэдр
12
12
4-6+4=2
6
8
8-12+6=2
30
20
n - угольная призма
6-12+8=2
20
30
2 n
12-30+20=2
12
3n
n-2
20-30+12=2
2n-3n+n+2=2
Существует следующая закономерность, что если
В - число вершин,
Р - число ребер,
Г - число граней,
то
В-Р+Г=2 ,
данное равенство выражает Эйлерову характеристику.
Равенство было доказано Эйлером в 1752 году и справедливо для всех произвольных выпуклых многогранников.

Многогранник называется правильным , если все его грани - равные правильные многоугольники.
К каждой вершине правильного многогранника сходится одно и то же число рёбер.
Сумма плоских углов при вершине правильных многогранников не больше пяти. Все двугранные углы при рёбрах и все многогранные углы при вершинах правильного многогранника равны.
Доказано, что правильных многогранников только 5 типов:
четырёхгранник (тетраэдр),
шестигранник или куб ( гексаэдр),
восьмигранник (октаэдр),
двенадцатигранник (додекаэдр),
двадцатигранник (икосаэдр).

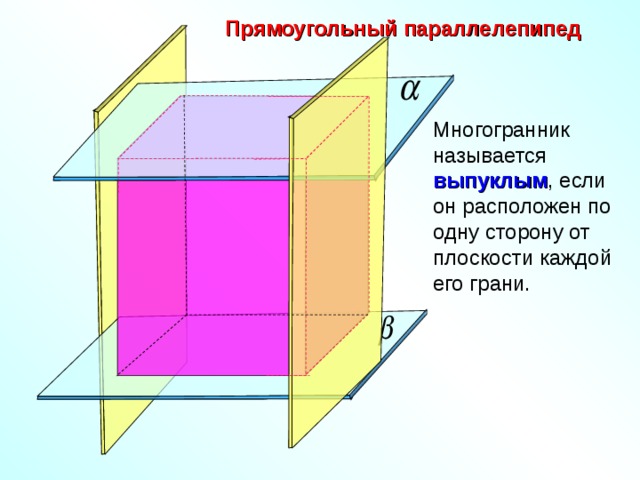
Прямоугольный параллелепипед
Многогранник называется выпуклым , если он расположен по одну сторону от плоскости каждой его грани.
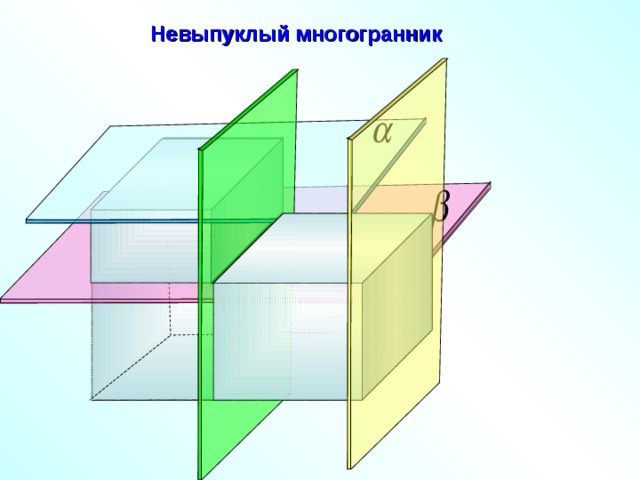
Невыпуклый многогранник
Г.В. Дорофеев, Л.Г. Петерсон, 6 класс (часть 3 ). № 7 42 ( а)
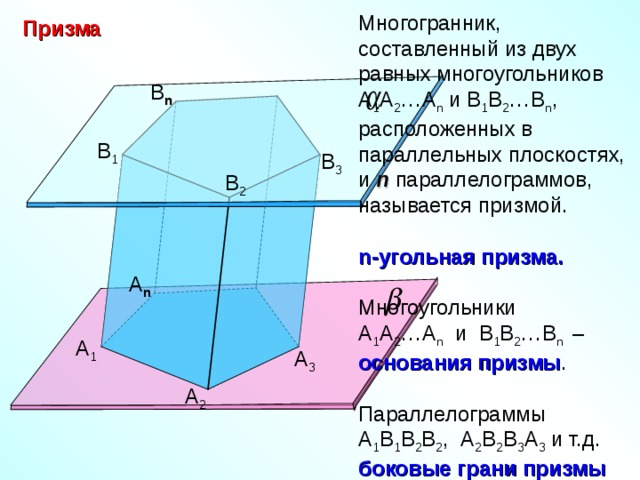
Многогранник, составленный из двух равных многоугольников А 1 А 2 …А n и В 1 В 2 …В n , расположенных в параллельных плоскостях, и n параллелограммов, называется призмой.
n -угольная призма.
Многоугольники
А 1 А 2 …А n и В 1 В 2 …В n – основания призмы .
Параллелограммы А 1 В 1 В 2 В 2 , А 2 В 2 В 3 А 3 и т.д. боковые грани призмы
Призма
B n
B 1
B 3
B 2
А n
А 1
А 3
А 2
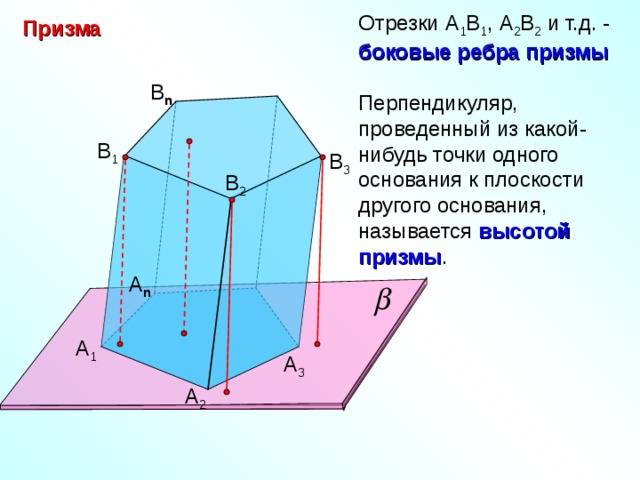
Отрезки А 1 В 1 , А 2 В 2 и т.д. -
боковые ребра призмы
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы .
Призма
B n
B 1
B 3
B 2
А n
А 1
А 3
А 2
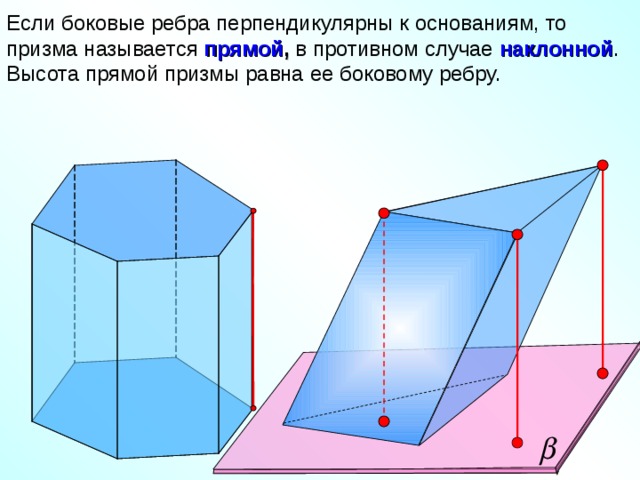
Если боковые ребра перпендикулярны к основаниям, то призма называется прямой , в противном случае наклонной .
Высота прямой призмы равна ее боковому ребру.
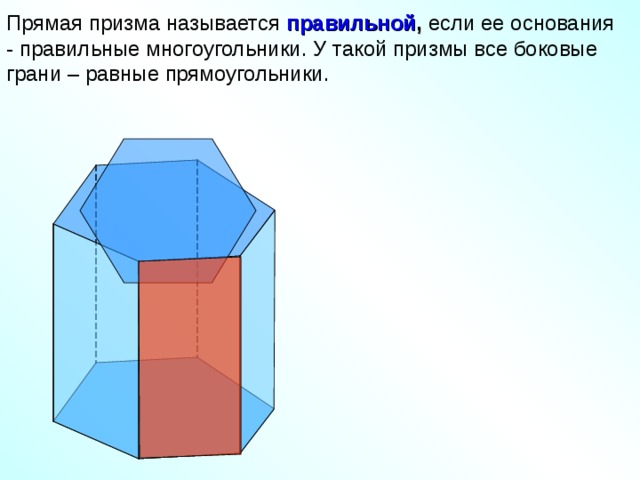
Прямая призма называется правильной , если ее основания - правильные многоугольники. У такой призмы все боковые грани – равные прямоугольники.
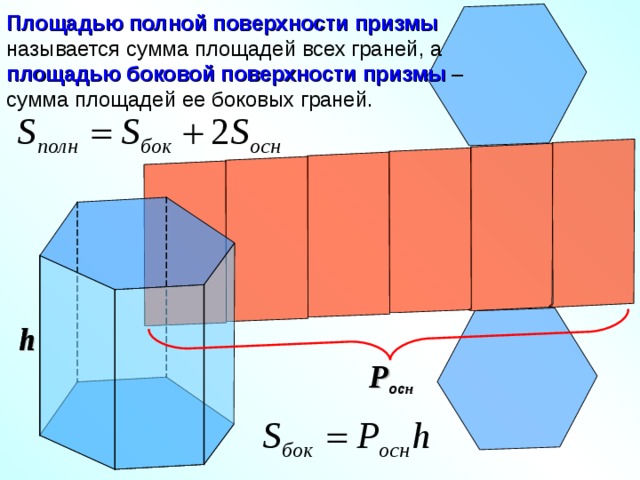
Площадью полной поверхности призмы называется сумма площадей всех граней, а площадью боковой поверхности призмы – сумма площадей ее боковых граней.
h
h
P oc н
5 см
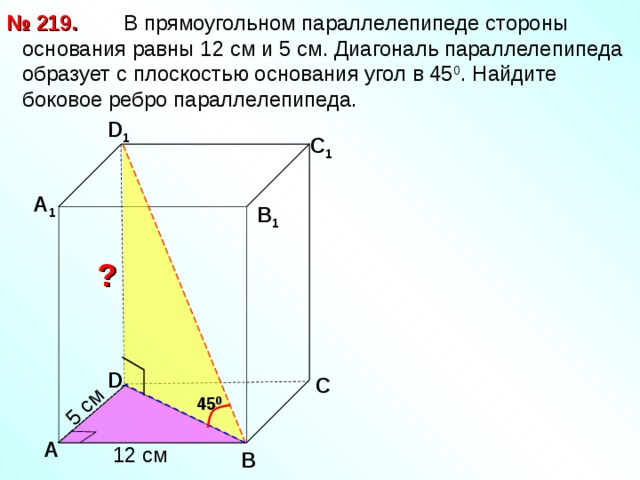
В прямоугольном параллелепипеде стороны основания равны 12 см и 5 см. Диагональ параллелепипеда образует с плоскостью основания угол в 45 0 . Найдите боковое ребро параллелепипеда.
№ 219.
D 1
С 1
А 1
В 1
?
D
С
45 0
А
12 см
В
24
10
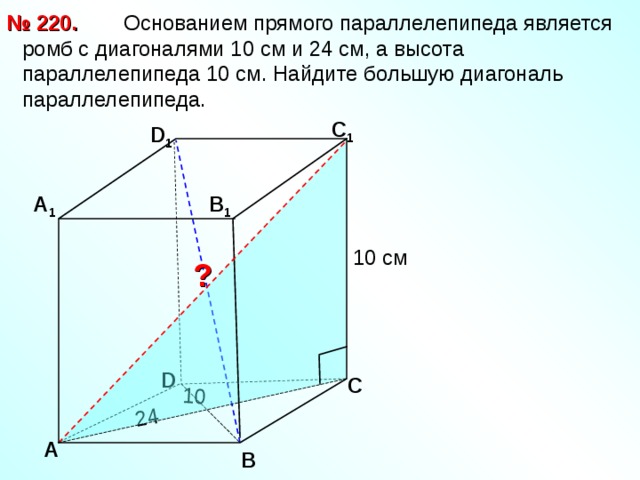
Основанием прямого параллелепипеда является ромб с диагоналями 10 см и 24 см, а высота параллелепипеда 10 см. Найдите большую диагональ параллелепипеда.
№ 220.
С 1
D 1
А 1
В 1
10 см
?
D
С
А
В
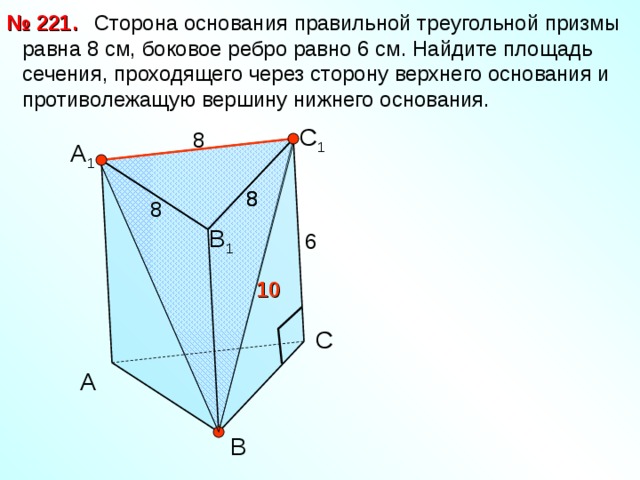
Сторона основания правильной треугольной призмы равна 8 см, боковое ребро равно 6 см. Найдите площадь сечения, проходящего через сторону верхнего основания и противолежащую вершину нижнего основания.
№ 22 1 .
С 1
8
А 1
8
8
8
В 1
6
10
С
А
В
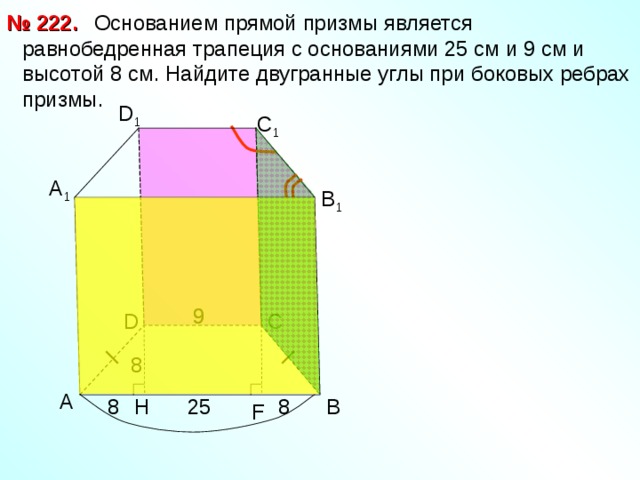
Основанием прямой призмы является равнобедренная трапеция с основаниями 25 см и 9 см и высотой 8 см. Найдите двугранные углы при боковых ребрах призмы.
№ 22 2 .
D 1
С 1
А 1
В 1
9
9
С
D
8
А
8
8
25
В
H
F
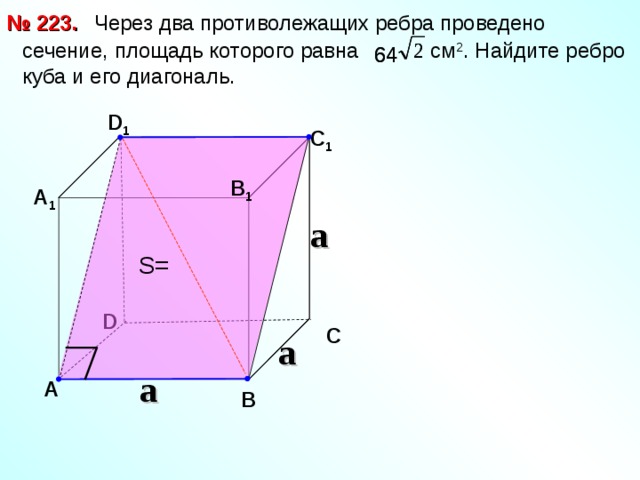
Через два противолежащих ребра проведено
сечение, площадь которого равна см 2 . Найдите ребро куба и его диагональ.
№ 223.
64
64
D 1
С 1
В 1
А 1
a
S=
D
С
a
a
А
В
a 2
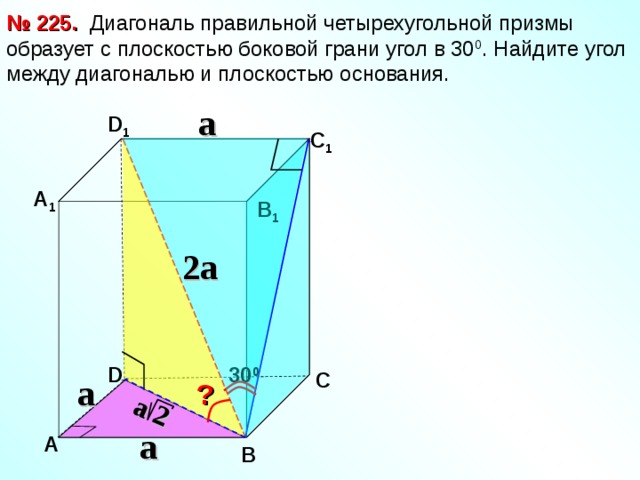
№ 225.
Диагональ правильной четырехугольной призмы образует с плоскостью боковой грани угол в 30 0 . Найдите угол между диагональю и плоскостью основания.
a
D 1
С 1
А 1
В 1
2 a
D
30 0
С
a
?
a
А
В
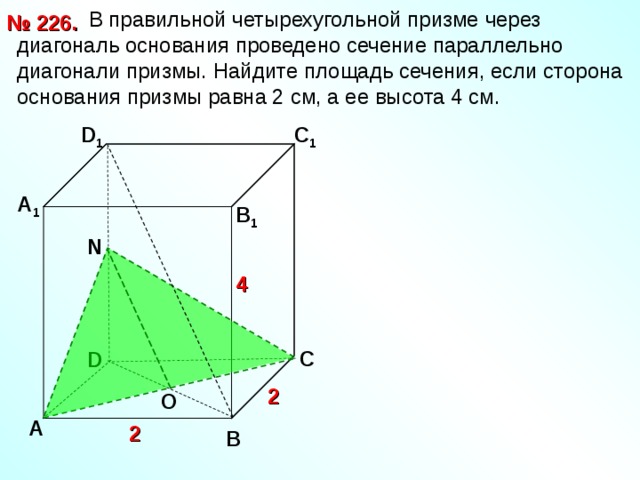
В правильной четырехугольной призме через диагональ основания проведено сечение параллельно диагонали призмы. Найдите площадь сечения, если сторона основания призмы равна 2 см, а ее высота 4 см.
№ 226.
D 1
С 1
А 1
В 1
N
4
С
D
2
O
А
2
В
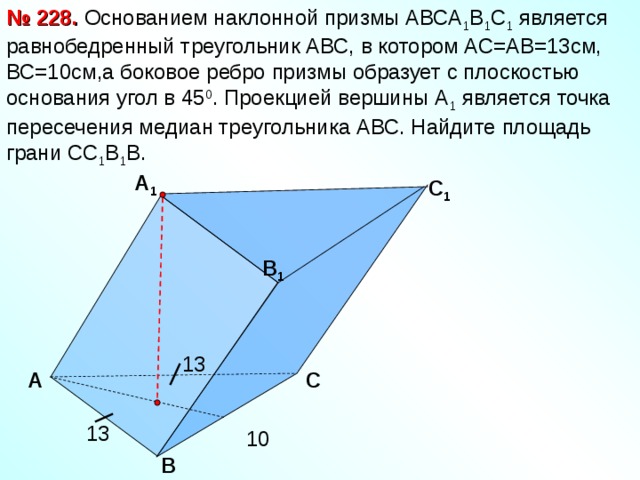
№ 228.
Основанием наклонной призмы АВСА 1 В 1 С 1 является равнобедренный треугольник АВС, в котором АС=АВ=13см, ВС=10см,а боковое ребро призмы образует с плоскостью основания угол в 45 0 . Проекцией вершины А 1 является точка пересечения медиан треугольника АВС. Найдите площадь грани СС 1 В 1 В.
А 1
C 1
B 1
13
А
C
13
10
B
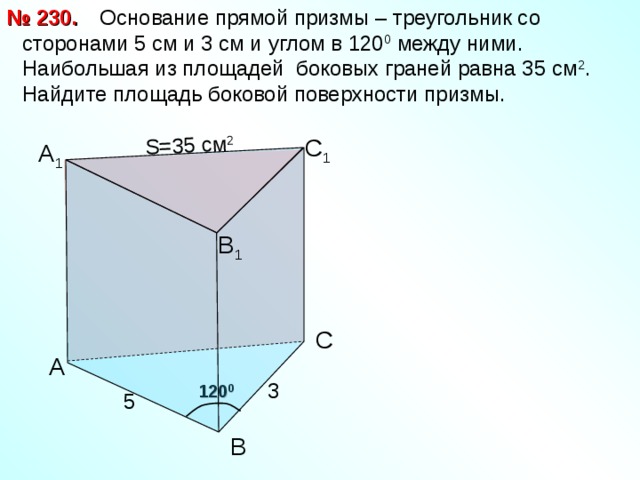
Основание прямой призмы – треугольник со сторонами 5 см и 3 см и углом в 120 0 между ними. Наибольшая из площадей боковых граней равна 35 см 2 . Найдите площадь боковой поверхности призмы.
№ 230.
S= 35 см 2
С 1
А 1
В 1
С
А
3
120 0
5
В





