Методическая разработка урока математики
по теме «Показательная функция. Свойства. График»
Тип урока: урок изучения и первичного закрепления нового материала.
Дидактическая цель: создать условия для осознания и осмысления блока новой учебной информации и способов ее получения средствами уровневой самостоятельной работы.
Цели по содержанию:- общеобразовательные
ввести понятие показательной функции и ее свойства
формировать умения различать показательную функцию
формировать умения по решению уравнений и неравенств с применением свойств показательной функции
развивающие
развитие логического мышления и культуры математической речи обучающихся
воспитательные
формирование графической культуры
воспитание у обучающихся настойчивости, целеустремленности, аккуратности
Средства: учебник, классная доска, дидактические карточки.
Опорные знания:
| Новые знания:
|
Опорные умения:
| Новые умения:
|
Ход урока:
| Этапы урока | Деятельность учителя | Деятельность учащихся |
1.Орг. момент
| Проверка готовности учащихся к учебной деятельности. | Приветствуют учителя |
2.Целепо- лагание и мотивация | Тема урока «Показательная функция». Разъясняет уровневые цели урока: 1) знать определение показательной функции, её свойства, уметь строить график; 2) научиться описывать свойства показательной функций по графику; 3) уметь применять свойства показательной функции при решении уравнений и неравенств графическим способом. Достижение первой цели гарантирует оценку «3», достижение первой и второй целей позволяет получить оценку «4», если освоили все три цели, то можете претендовать на оценку «5».
| Слушают учителя.
Ставят перед собой цель на урок |
3. Актуализация знаний | Входная диагностическая работа № 1.
а) у = 2х б) у = х2 в) у = х3 г) у = х + 1 д) у = 3 – х
функциям: б) в) г) а) а)
| Фронтальная работа |
4. Первичное усвоение материала | у =2х - это новая функция и называется показательной функцией. Функция, заданная формулой у = ах , где а 0 и а Свойства: 1) D(у) = 2) Е(у) = 3) При а 1 функция возрастает на всей числовой прямой, при 0 числовой прямой. 4) При любых действительных значениях х и у справедливы основные свойства степеней. Для построения графика показательной функции воспользуемся табличным способом. - Объясняет построение графиков функций у = 2х и у = Что общего есть у этих графиков? Запишите свойства этих функций. Умение выполнять задания такого типа гарантирует вам оценку «3» по данной теме.
Более сложное задание: построить схематично график функции и определить область значения функции (№ 446 (а, б)): а) у = – 2х ; б) у = - Объясняет решение № 446
Ещё более сложный уровень: решить графически уравнение 3х = 4 – х (№ 457 а) - Объясняет решение № 457
| Слушают учителя, записывают в тетрадь определение и свойства показательной функции.
Выполняют построение в тетради.
Записывают решение № 446 в тетрадь
Записывают решение № 457 в тетрадь
|
5. Осознание и осмысление
Уровень различения
Уровень запоминания
Уровень понимания
Уровень применения
| Проверим уровень усвоения вами нового материала. Диагностическая работа № 2.
1)Определите, какие функции являются показательными: а) у = 3х ; б) у = 3х ; в) у = д) у = 0,3х ; е) у = 0,3 + х 2) Ответьте на вопросы: а) Что такое показательная функция? б) Какова область определения показательной функции? в) Какова область значения показательной функции? г) При каких условиях функция является возрастающей, убывающей? 3) Верны ли эти утверждения для показательной функции: а) а б) D(у) = в) Е(у) = г) Показательная функция является возрастающей при любом а. Оцените свою работу. 4) Постройте график функции у = 4х и перечислите её свойства.
|
Отвечают устно
Отвечают устно
Выполняют в тетрадях
Взаимопроверка
Выполняют в тетрадях Самопроверка по образцу |
6. Первичное закрепление | Если вы справились с заданием 4) самостоятельно, то выполняете № 2. Если вы не справились с заданием 4), то выполняете № 1 вместе с учителем. Если вы справились с № 2 , то выполняете № 3
№ 1. Построить график функции у = и перечислить её свойства. № 2. Решите № 446(в, г) № 3. Найти наибольшее целое решение неравенства
Диагностическая работа № 3(выходная диагностика). 1. Укажите график функции заданной формулой: I в. у = 3х II в. у =
а) б)
г
д в)
2. Укажите D(f) и E(f) для функций I в. f(x) = a) D(f) = Е(f) = в) D(f) = E(f) = 3. Из данных функций выберите I в. убывающие II в. возрастающие а) у = 2х б) у = е) у =
4. Укажите функцию, областью значений которой является множество I в. Е(у) = а) у = 3х ; б) у = 3х + 1; в) у = 3х – 1 ; г) у = 3х + 2 ; д) у = 3х – 2 5. Для функции f (x) = 3х укажите такие функции g(x), что уравнение f(x) = g(x) имеет ровно один корень. а) g(x) = г) g(x) = 2 | Каждый учащийся работает на своём уровне
Выполняют работу на листочках
Взаимопроверка Критерии оценивания: «3» - верно выполнены 1,2,3 «4» - верно выполнены 1,2,3,4 «5» - верно выполнены 1,2,3,4,5
|
7. Домашнее задание | Обязательная часть: № 445(в, г) («3») № 457 (б) Необязательная часть: № 458(б) (оценивается отдельно)
| Записывают домашнее задание |
8. Рефлексия | Вспомните, какие цели вы ставили перед собой в начале урока. Определите уровень своих достижений. Дополните предложения: сегодня на уроке я узнал …, я научился…, самым лёгким для меня было… , самым трудным для меня было….
| Отвечают на вопросы учителя, делают вывод о качестве усвоения материала. |

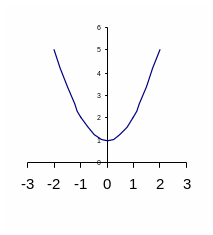
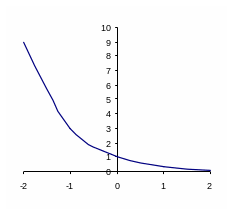
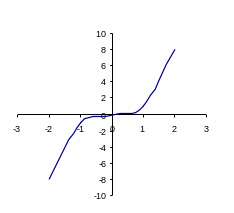 айдите графики, которые соответствуют данным
айдите графики, которые соответствуют данным 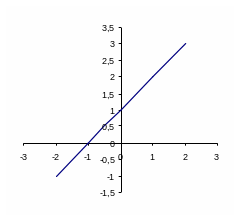
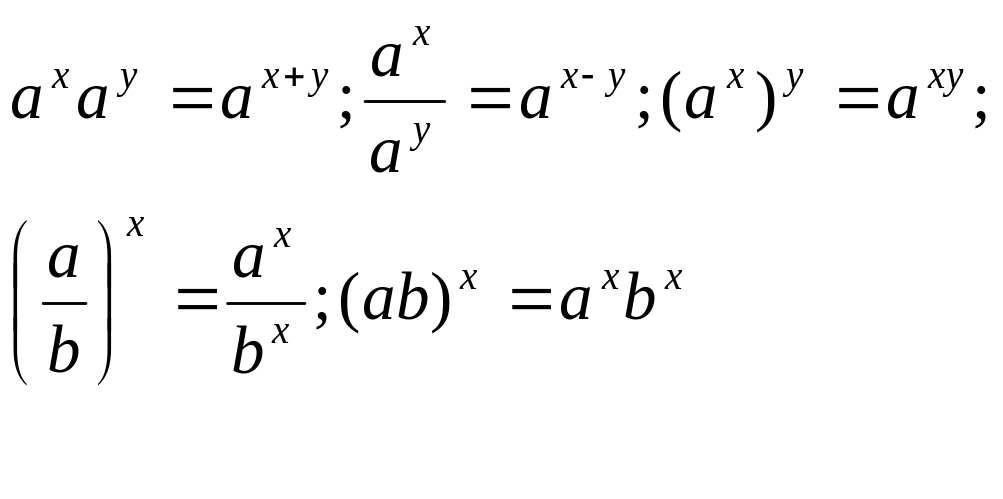
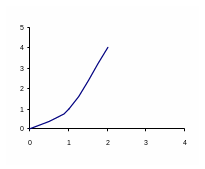
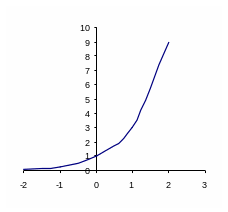 )
)