тема урока:
Показательная функция, ее свойства и график.
0 , a 1) , называется показательной функцией с основанием а у=а x 0 у=а x a1 х х ГРАФИК - ЭКСПОНЕНТА" width="640"
Определение
- Функция, заданная формулой у=а x ( где а 0 , a 1) , называется показательной функцией с основанием а
у=а x
0
у=а x
a1
х
х
ГРАФИК - ЭКСПОНЕНТА
1 Область определения – множество всех действительных чисел D(y) = R ; Ни чётная, ни нечётная; Нет ни наибольшего, ни наименьшего значений; у=а x a1 х ЭКСПОНЕНТА" width="640"
Свойства показательной функции у=а x при а 1
- Область определения – множество всех действительных чисел D(y) = R ;
- Ни чётная, ни нечётная;
- Нет ни наибольшего, ни наименьшего значений;
у=а x
a1
х
ЭКСПОНЕНТА
1 Область значений – множество всех положительных чисел E( y )= R + ; Ограничена снизу; Непрерывна; у=а x a1 х ЭКСПОНЕНТА" width="640"
Свойства показательной функции у=а x при а 1
- Область значений – множество всех положительных чисел E( y )= R + ;
- Ограничена снизу;
- Непрерывна;
у=а x
a1
х
ЭКСПОНЕНТА
1 у=а x a1 Функция возрастает на всей области определения; Выпукла вниз; х ЭКСПОНЕНТА" width="640"
Свойства показательной функции у=а x при а 1
у=а x
a1
- Функция возрастает на всей области определения;
- Выпукла вниз;
х
ЭКСПОНЕНТА
1 у=а x a1 При х =0 значение функции равно 1 х ЭКСПОНЕНТА" width="640"
Свойства показательной функции у=а x при а 1
у=а x
a1
- При х =0 значение функции равно 1
х
ЭКСПОНЕНТА
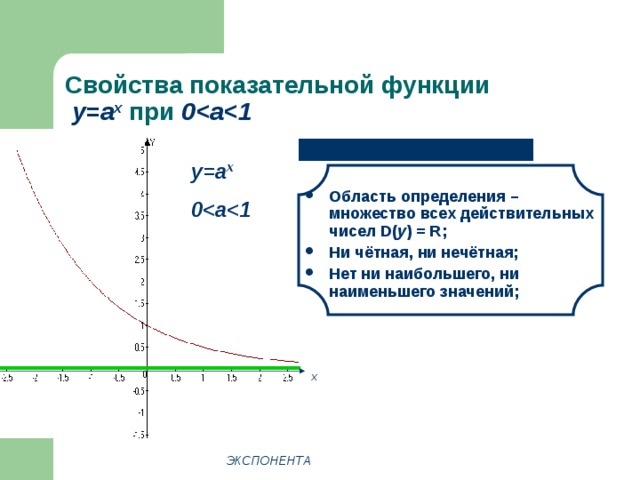
Свойства показательной функции у=а x при 0
у=а x
0
- Область определения – множество всех действительных чисел D( y ) = R ;
- Ни чётная, ни нечётная;
- Нет ни наибольшего, ни наименьшего значений;
х
ЭКСПОНЕНТА
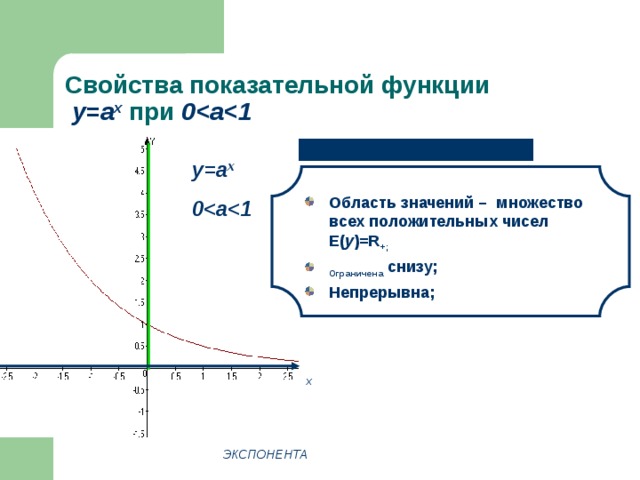
Свойства показательной функции у=а x при 0
у=а x
0
- Область значений – множество всех положительных чисел E( y )=R + ;
- Ограничена снизу;
- Непрерывна;
х
ЭКСПОНЕНТА
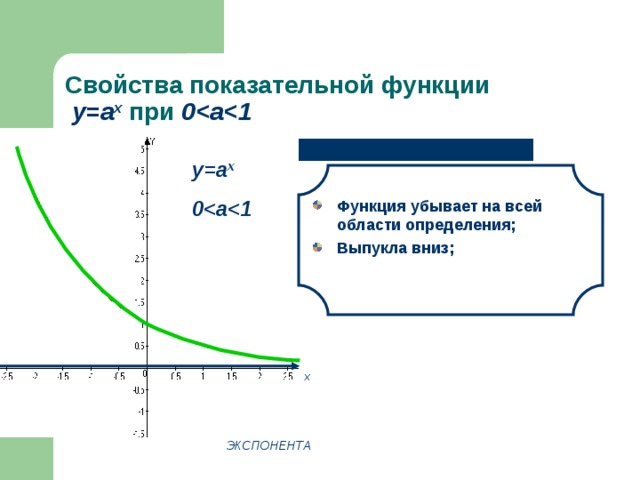
Свойства показательной функции у=а x при 0
у=а x
0
- Функция убывает на всей области определения;
- Выпукла вниз;
х
ЭКСПОНЕНТА
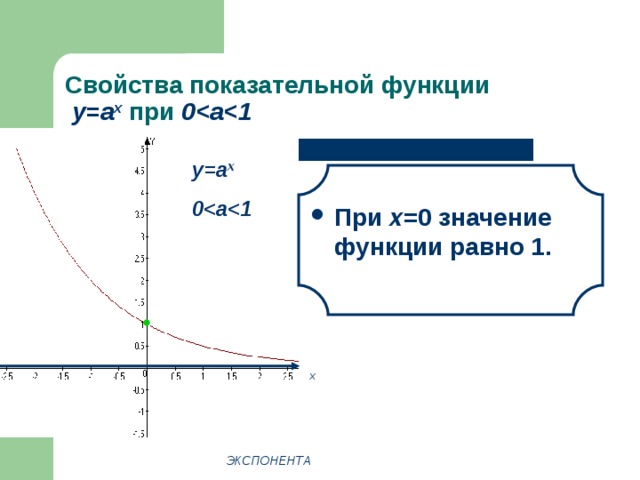
Свойства показательной функции у=а x при 0
у=а x
0
- При х =0 значение функции равно 1.
х
ЭКСПОНЕНТА
Показательные уравнения
не имеет корней
