Практична робота № 1
Перетворення чисел із однієї системи числення в іншу
Мета роботи: навчитися перетворювати числа із однієї системи числення в іншу.
1.1 Теоретичні відомості
1.1.1 Поняття системи числення
Система числення – це спосіб запису чисел за допомогою заданого набору спеціальних знаків (цифр).
Існують позиційні і непозиційні системи числення.
У непозиційних системах вага цифрине залежить від її позиції в записі числа. Так, в римській системі числення в числі ХХХII (тридцять два) вага цифри Х в будь-якій позиції дорівнює просто десяти.
У позиційних системах числення вага кожної цифри змінюється залежно від її положення (позиції) в послідовності цифр, що зображують число.
Наприклад, в числі 757,7 перша сімка означає 7 сотень, друга – 7 одиниць, а третя – 7 десятих доль одиниці.
Сам же запис числа 757,7 означає скорочений запис виразу:
700 + 50 + 7 + 0,7 = 7*102 + 5*101 + 7*100 + 7*10-1 = 757,7.
Будь-яка позиційна система числення характеризується своєю основою.
Основа позиційної системи числення – це кількість різних знаків або символів, що використовуються для зображення цифр в даній системі.
За основу системи можна прийняти будь-яке натуральне число – два, три, чотири і так далі. Отже, можлива нескінченна множина позиційних систем: двійкова, трійкова, четверична тощо. Запис чисел в кожній з систем числення з основою q означає скорочений запис виразу:
an-1 qn-1 + an-2 qn-2+ ... + a1 q1 + a0 q0 + a-1 q-1 + ... + a-m q-m,
де ai– цифри системи числення;
n і m – число цілих і дробових розрядів, відповідно.
Вага розряду Рi числа в позиційній системі числення – це відношення 
, де i номер розряду зправа наліво.
Вага розрядів росте зправа наліво. Якщо візьмемо розряд Рі=10к , то наступний старший буде мати вагу Pi+1=10K+1, а молодший Pi–1=10K–1. Такий взаємозв’язок розрядів передбачає, при виконанні операцій, передачу інформації між ними. Якщо в даному розряді накопичилося значення одиниць, що дорівнює або більше q, то повинна відбуватися передача одиниці в сусідній старший розряд.
Наприклад:
У кожній системі числення цифри впорядковані відповідно до їх значень: 1 більше 0, 2 більше 1 і так далі.
Просуванням цифри називають заміну її наступною по величині.
Просунути цифру 1 означає замінити її на 2, просунути цифру 2 означає замінити її на 3 і так далі. Просування старшої цифри (наприклад, цифри 9 в десятковій системі) означає заміну її на 0. У двійковій системі, що використовує лише дві цифри, – 0 і 1, просування 0 означає заміну її на 1, а просування 1 – заміну її на 0.
Цілі числа в будь-якій системі числення породжуються за допомогою Правила рахунку: для утворення цілого числа, наступного за будь-яким даним цілим числом, потрібно просунути найправішу цифру числа; якщо яка-небудь цифра після просування стала нулем, то потрібно просунути цифру, що стоїть зліва від неї.
Застосовуючи це правило, запишемо перші десять цілих чисел у різних системах числення:
у двійковій системі: 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001;
у трійковій системі: 0, 1, 2, 10, 11, 12, 20, 21, 22, 100;
у п’ятирічній системі: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14;
вісімковій системі: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11.
Окрім десяткової широко використовуються системи з основою, що є цілою степінню числа 2, а саме:
двійкова (використовуються цифри 0, 1);
вісімкова (використовуються цифри 0, 1, ..., 7);
шістнадцятирічна (для перших цілих чисел від нуля до дев’яти використовуються цифри 0, 1, ..., 9, а для наступних чисел – від десяти до п’ятнадцяти – як цифри використовуються символи A, B, C, D, E, F).
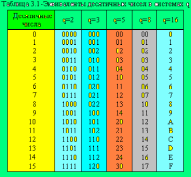
Дані системи числення наводяться у таблиці 1.1.
Вибір системи числення обумовлюється наступними причинами:
основа системи визначає число знаків, що представляються в одному розряді. Тут перевагу має двійкова система, а не десяткова оскільки вона потребує всього два знаки (0,1);
система числень повинна забезпечити точність арифметики, великий діапазон і простоту представлення чисел. Сигнал передачі біта інформації і майже всі радіоелементи мають двійкову природу і легко відображують числа в двійковій системі.
система числень повинна забезпечити точність арифметики, великий діапазон і простоту представлення чисел. Сигнал передачі біта інформації і майже всі радіоелементи мають двійкову природу і легко відображують числа в двійковій системі.
Таблиця 1.1 – Еквіваленти десяткових чисел у різних системах
Тому, із усіх систем числення особливо проста і тому цікава для технічної реалізації в комп’ютерах двійкова система числення.
Люди віддають перевагу десятковій системі, ймовірно, тому, що з давніх часів рахували по пальцях, а пальців у людей по десять на руках і ногах. Не завжди і не скрізь люди користуються десятковою системою числення. У Китаї, наприклад, довгий час користувалися п’ятирічною системою числення.
А комп’ютери використовують двійкову систему тому, що вона має ряд переваг перед іншими системами:
для її реалізації потрібні технічні пристрої з двома стійкими станами (є струм – немає струму, намагнічений – не намагнічений і тому подібне), а не, наприклад, з десятьма, – як в десятковій;
представлення інформації за допомогою лише двох станів надійно і завадостійко;
можливе застосування апарату булевої алгебри для виконання логічних перетворень інформації;
двійкова арифметика набагато простіша за десяткову.
Недоліком двійкової системи є швидке зростання числа розрядів, необхідних для запису чисел.
Двійкова система, зручна для комп’ютерів, для людини незручна із-за її громіздкості й незвичного запису.
Переведення чисел з десяткової системи в двійкову і навпаки виконує машина. Проте, аби професійно використовувати комп’ютер, слід навчитися розуміти слово машини. Для цього і розроблені вісімкова і шістнадцятирічна системи.
Числа в цих системах читаються майже так само легко, як в десятковій, які потребують відповідно в три (вісімкова) і в чотири (шістнадцятирічна) рази менше розрядів, чим в двійковій системі (адже числа 8 і 16 – відповідно, третя і четверта степені числа 2).
1.1.2 Правила переведення чисел із однієї позиційної системи числення в іншу
1.1.2.1 Переведення числа із десяткової системи в будь-яку іншу позиційну систему числення
При переведенні чисел з десяткової системи числення в систему з основою P 1 зазвичай використовують наступний алгоритм:
1) Якщо переводиться ціла частина числа, то вона ділиться на P, після чого запам’ятовується залишок від ділення. Отримана частка знову ділиться на P, залишок запам’ятовується. Процедура продовжується доти, доки частка не стане рівною нулю. Залишки від ділення на P виписуються в порядку, зворотньому їх отриманню.
2) Якщо переводиться дробова частина числа, то вона множиться на P, після чого ціла частина запам’ятовується і відкидається. Знов отримана дробова частина множиться на P і так далі. Процедура продовжується доти, доки дробова частина не стане рівною нулю. Цілі частини виписуються після двійкової коми в порядку їх отримання. Результатом може бути або кінцевий, або періодичний двійковий дріб. Тому, коли дріб є періодичним, доводиться обривати множення на деякому кроці і задовольнятися наближеним записом вихідного числа в системі з основю P.
Приклад 1. Перевести число 75 з десяткової системи в двійкову, вісімкову і шістнадцятирічну.
Рішення:
Відповідь: 7510 = 1 001 0112 = 1138 = 4B16.
Приклад 2. Перевести число 0,35 з десяткової системи в двійкову, вісімкову і шістнадцятирічну.
Рішення:
Відповідь: 0,3510 = 0,010112 = 0,2638 = 0,5916 .
Приклад 3. Перевести дане число з десяткової системи числення в двійкову отримати п’ять знаків після коми в двійковому представленні).
а) 464(10); б) 380,1875(10); в) 115,94(10)
Рішення:
| а) 464 | 0 |
| б) 380 | 0 |
| 1875 |
| в) 115 | 1 |
| 94 |
| 232 | 0 |
| 190 | 0 | 0 | 375 |
| 57 | 1 | 1 | 88 |
| 116 | 0 |
| 95 | 1 | 0 | 75 |
| 28 | 0 | 1 | 76 |
| 58 | 0 |
| 47 | 1 | 1 | 5 |
| 14 | 0 | 1 | 52 |
| 29 | 1 |
| 23 | 1 | 1 | 0 |
| 7 | 1 | 1 | 04 |
| 14 | 0 |
| 11 | 1 |
|
|
| 3 | 1 | 0 | 08 |
| 7 | 1 |
| 5 | 1 |
|
|
| 1 | 1 | 0 | 16 |
| 3 | 1 |
| 2 | 0 |
|
|
|
|
|
|
|
| 1 | 1 |
| 1 | 1 |
|
|
|
|
|
|
|
Відповідь: а) 464(10)=111010000(2); б) 380,1875(10) = 101111100,0011(2);
в) 115,94(10) 1110011,11110(2) (в даному випадку було отримано шість знаків після коми, після чого результат був заокруглений).
1.1.2.2 Переведення чисел із двійкової (вісімкової, шістнадцятирічної) системи в двійкову систему числення та навпаки
Якщо необхідно перевести число з двійкової системи числення в систему числення, основою якої є степінь двійки, досить об’єднати цифри двійкового числа в групи по стільки цифр, яким є показник степеня, і застосувати наведений нижче алгоритм.
Наприклад, якщо переклад здійснюється у вісімкову систему, то групи будуть містити по три цифри (8 = 23). У цілій частині числа групування проводиться зправа наліво, в дробовій частині – зліва направо. Якщо в останній групі бракує цифри, дописуються нулі: у цілій частині – зліва, в дробі – зправа. Потім кожна група замінюється відповідною цифрою нової системи. Відповідності наведені в таблиці 1.2.
Таблиця 1.2 – Відповідності систем числення
| P | Відповідності | |||||||||||||||
| 2 | 00 | 01 | 10 | 11 |
| |||||||||||
| 4 | 0 | 1 | 2 | 3 |
| |||||||||||
| 2 | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
| |||||||
| 8 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|
|
|
|
|
|
|
|
| 2 | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
| 16 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
Переведемо з двійкової системи в шістнадцятиричну число 1111010101,11(2):
0011 1101 0101,1100(2) = 3D5,C(16).
Переведення восьмирічних та шістнадцятирічних чисел в двійкову систему дуже простий: достатньо кожну цифру замінити еквівалентною їй двійковою тріадою (трійкою цифр) або тетрадою (четвіркою цифр).
Наприклад:
Щоб перевести число з двійкової системи у вісімкову або шістнадцятиричну, його потрібно розбити вліво і вправо від коми на тріади (для вісімкової) або тетради (для шістнадцятиричної) і кожну таку групу замінити відповідною вісімковою (шістнадцятирічною) цифрою.
Наприклад:
1.1.2.3 Пеpеведення чисел із двійкової, вісімкової та шістнадцятирічної системи числення в десяткову систему числення
При переведенні числа з двійкової (вісімкової, шістнадцятирічної) системи в десяткову треба це число представити у вигляді суми степенів основи її системи числення.
При переведенні чисел з системи числення з основою P в десяткову систему числення необхідно пронумерувати розряди цілої частини зправа наліво, починаючи з нульового, і дробової частини, починаючи з розряду відразу після коми, зліва направо (початковий номер –1). Потім обчислити суму добутків відповідних значень розрядів на основу системи числення в степені, що дорівнює номеру розряду. Це і є представлення вихідного числа в десятковій системі числення.
Наприклад:
Приклад 4. Перевести дане число в десяткову систему числення:
а) 1000001(2).
1000001(2) = 1 * 26 + 0 * 25 + 0 * 24 + 0 * 23 + 0 * 22 + 0 * 21 + 1 * 20 =
= 64 + 1 = 65(10).
Зауваження. Якщо в будь-якому розряді стоїть нуль, то відповідний доданок можна опускати.
б) 1000011111,0101(2).
1000011111,0101(2) = 1 29 + 1 24 + 1 23 + 1 22 + 1 21 + 1 20 + 1 2–2+ + 1 2–4 = 512 + 16 + 8 + 4 + 2 + 1 + 0,25 + 0,0625 = 543,3125(10).
в) 1216,04(8).
1216,04(8) = 1 83 + 2 82 + 1 81 + 6 80 + 4 8–2 = 512 + 128 + 8 + 6 + 0,0625=
= 654,0625(10).
г) 29A,5(16).
29A,5(16) = 2 162 + 9 161 + 10 160 + 5 16–1 = 512 + 144 + 10 + 0,3125=
= 656,3125(10).
Зведена таблиця переведення цілиых чисел із однієї системи числення в іншу подається у табл. 3.
Таблица 1.3 – Зведена таблиця переведення цілих чисел
1.2 Завдання до виконання практичної роботи №1
Із додатку Б згідно свого номера в журналі студент обирає варіант для виконання завдань практичної роботи №1.
У зошиті для практичних робіт (можна за допомогою комп’ютера, а потім роздрукувати у вигляді звіту) проводиться переведення чисел в задані системи числення з обов’язковим виконанням перевірки. Виконуються лише 1 та 2 завдання:
Перше завдання – Перевести задане число із десяткової системи числення в двійкову, вісімкову та шістнадцяткову системи числення.
Друге завдання – Перевести задане число в десяткову систему числення.
1.3 Контрольні питання
Дайти визначення системи числення. Назвати і охарактеризувати властивості системи числення.
Які системи числення називаються позиційними, а які – непозиційними? Наведіть приклади.
Що називається основою системи числення?
Чому для обчислювальної техніки особливо важлива двійкова система числення?
Які способи переведення цілих десяткових чисел в двійкові і навпаки Ви знаєте?
Як переводити цілі числа з двійкової системи числення у вісімкову і шістнадцятирічну і назвпаки?
Які символи використовуються для запису чисел в двійковій системі числення, вісімковій, шістнадцятиричній?
Чому дорівнюють ваги розрядів зліва від коми, що розділяє цілу і дробову частину, в двійковій системі числення (вісімковою, шістнадцятирічною)?
Чому дорівнюють ваги розрядів праворуч від коми, що розділяє цілу і дробову частину, в двійковій системі числення (вісімковою, шістнадцятирічною)?
| Завдання | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 14 | ||
| Відмітка про виконання |
|
|
|
|
|
|
|
|
|
|
|
|
| ||
| Дата виконання |
| Оцінка |
| Підпис викладача |
| ||||||||||
ДОДАТОК Б
Варіанти завдань до практичної роботи №1
Варіант 1
1. а) 860(10); б) 785(10); в) 149,375(10); г) 953,25(10); д) 228,79(10).
2. а) 1001010(2); б) 1100111(2); в) 110101101,00011(2); г) 111111100,0001(2); д) 775,11(8); е) 294,3(16).
Варіант 2
1. а) 250(10); б) 757(10); в) 711,25(10); г) 914,625(10); д) 261,78(10).
2. а) 1111000(2); б) 1111000000(2); в) 111101100,01101(2); г) 100111100,1101(2); д) 1233,5(8);
Варіант 3
1. а) 759(10); б) 265(10); в) 79,4375(10); г) 360,25(10); д) 240,25(10).
2. а) 1001101(2); б) 10001000(2); в) 100111001,01(2); г) 1111010000,001(2); д) 1461,15(8); е) 9D,A(16).
Варіант 4
1. а) 216(10); б) 336(10); в) 741,125(10); г) 712,375(10); д) 184,14(10).
2. а) 1100000110(2); б) 1100010(2); в) 1011010,001(2); г) 1010100010,001(2); д) 1537,22(8); е) 2D9,8(16).
Варіант 5
1. а) 530(10); б) 265(10); в) 597,25(10); г) 300,375(10); д) 75,57(10).
2. а) 101000111(2); б) 110001001(2); в) 1001101010,01(2); г) 1011110100,01(2); д) 1317,75(8); е) 2F4,0C(16).
Варіант 6
1. а) 945(10); б) 85(10); в) 444,125(10); г) 989,375(10); д) 237,73(10).
2. а) 110001111(2); б) 111010001(2); в) 100110101,1001(2); г) 1000010,01011(2); д) 176,5(8); е) 3D2,04(16).
Варіант 7
1. а) 287(10); б) 220(10); в) 332,1875(10); г) 652,625(10); д) 315,21(10).
2. а) 10101000(2); б) 1101100(2); в) 10000010000,01001(2); г) 1110010100,001(2); д) 1714,2(8); е) DD,3(16).
Варіант 8
1. а) 485(10); б) 970(10); в) 426,375(10); г) 725,625(10); д) 169,93(10).
2. а) 10101000(2); б) 101111110(2); в) 1010101,101(2); г) 1111001110,01(2); д) 721,2(8); е) 3C9,8(16).
Варіант 9
1. а) 639(10); б) 485(10); в) 581,25(10); г) 673,5(10); д) 296,33(10).
2. а) 1011000011(2); б) 100010111(2); в) 1100101101,1(2); г) 1000000000,01(2); д) 1046,4(8); е) 388,64(16).
Варіант 10
1. а) 618(10); б) 556(10); в) 129,25(10); г) 928,25(10); д) 155,45(10).
2. а) 1111011011(2); б) 1011101101(2); в) 1001110110,011(2); г) 1011110011,10111(2); д) 675,2(8); е) 94,4(16).
Варіант 11
1. а) 772(10); б) 71(10); в) 284,375(10); г) 876,5(10); д) 281,86(10).
2. а) 1000001111(2); б) 1010000110(2); в) 101100110,011011(2); г) 100100110,101011(2); д) 1022,2(8); е) 53,9(16).
Варіант 12
1. а) 233(10); б) 243(10); в) 830,375(10); г) 212,5(10); д) 58,89(10).
2. а) 1001101111(2); б) 1000001110(2); в) 111110011,011(2); г) 11010101,1001(2); д) 1634,5(8); е) C2,3(16).
Варіант 13
1. а) 218(10); б) 767(10); в) 894,5(10); г) 667,125(10); д) 3,67(10).
2. а) 1111100010(2); б) 1000011110(2); в) 101100001,011101(2); г) 1001111001,1(2); д) 1071,54(8); е) 18B,0C(16).
Варіант 14
1. а) 898(10); б) 751(10); в) 327,375(10); г) 256,625(10); д) 184,4(10).
2. а) 101110100(2); б) 1111101101(2); в) 1110100001,01(2); г) 1011111010,0001(2); д) 744,12(8); е) 1EE,C(16).
Варіант 15
1. а) 557(10); б) 730(10); в) 494,25(10); г) 737,625(10); д) 165,37(10).
2. а) 101001101(2); б) 1110111100(2); в) 10000001000,001(2); г) 1000110110,11011(2); д) 147,56(8); е) 1CA,3(16).
Варіант 16
1. а) 737(10); б) 92(10); в) 934,25(10); г) 413,5625(10); д) 100,94(10).
2. а) 1110000010(2); б) 1000100(2); в) 110000100,001(2); г) 1001011111,00011(2); д) 665,42(8); е) 246,18(16).
Варіант 17
1. а) 575(10); б) 748(10); в) 933,5(10); г) 1005,375(10); д) 270,44(10).
2. а) 1010000(2); б) 10010000(2); в) 1111010000,01(2); г) 101000011,01(2); д) 1004,1(8); е) 103,8C(16).
Варіант 18
1. а) 563(10); б) 130(10); в) 892,5(10); г) 619,25(10); д) 198,05(10).
2. а) 11100001(2); б) 101110111(2); в) 1011110010,0001(2); г) 1100010101,010101(2); д) 533,2(8); е) 32,22(16).
Варіант 19
1. а) 453(10); б) 481(10); в) 461,25(10); г) 667,25(10); д) 305,88(10).
2. а) 111001010(2); б) 1101110001(2); в) 1001010100,10001(2); г) 111111110,11001(2); д) 1634,35(8); е) 6B,A(16).
Варіант 20
1. а) 572(10); б) 336(10); в) 68,5(10); г) 339,25(10); д) 160,57(10).
2. а) 1010110011(2); б) 1101110100(2); в) 1010101,101(2); г) 1101000,001(2); д) 414,1(8); е) 366,4(16).
Варіант 21
1. а) 949(10); б) 763(10); в) 994,125(10); г) 523,25(10); д) 203,82(10).
2. а) 1110001111(2); б) 100011011(2); в) 1001100101,1001(2); г) 1001001,011(2); д) 335,7(8); е) 14C,A(16).
Варіант 22
1. а) 563(10); б) 264(10); в) 234,25(10); г) 53,125(10); д) 286,16(10).
2. а) 1100010010(2); б) 10011011(2); в) 1111000001,01(2); г) 10110111,01(2); д) 416,1(8); е) 215,7(16).
Варіант 23
1. а) 279(10); б) 281(10); в) 841,375(10); г) 800,3125(10); д) 208,92(10).
2. а) 1100111001(2); б) 10011101(2); в) 1111011,001(2); г) 110000101,01(2); д) 1601,56(8); е) 16E,B4(16).
Варіант 24
1. а) 744(10); б) 554(10); в) 269,375(10); г) 120,25(10); д) 139,09(10).
2. а) 101000001(2); б) 1110111100(2); в) 1001110101,011001(2); г) 1000010001,00011(2); д) 1177,6(8); е) 3FA,E8(16).
Варіант 25
1. а) 686(10); б) 585(10); в) 530,6875(10); г) 87,375(10); д) 131,82(10).
2. а) 110111001(2); б) 101111011(2); в) 1110111100,1(2); г) 110000011,0111(2); д) 742,34(8); е) 396,A(16).
Варіант 26
1. а) 679(10); б) 385(10); в) 981,25(10); г) 273,5(10); д) 796,33(10).
2. а) 1010000011(2); б) 100011111(2); в) 1100110101,1(2); г) 1010000000,01(2); д) 1036,4(8); е) 328,64(16).
Варіант 27
1. а) 618(10); б) 556(10); в) 129,25(10); г) 928,25(10); д) 155,45(10).
2. а) 1111011011(2); б) 1011101101(2); в) 1001110110,011(2); г) 1011110011,10111(2); д) 675,2(8); е) 94,4(16).
Варіант 28
1. а) 772(10); б) 71(10); в) 284,375(10); г) 876,5(10); д) 281,86(10).
2. а) 1000001111(2); б) 1010000110(2); в) 101100110,011011(2); г) 100100110,101011(2); д) 1022,2(8); е) 53,9(16).
