Обобщение опыта по теме «Создание проблемных ситуаций на уроках математики, как средство Развития умственной самостоятельности учащихся »
учитель математики
Семенова Т.В.
1. Информационный блок
1.1. Название темы опыта
Создание проблемных ситуаций на уроках математики как средство развития умственной самостоятельности учащихся.
1.2. Актуальность опыта
Актуальность опыта обусловлена, требованием времени, поскольку в современном обществе востребован выпускник, который отличается креативным мышлением, способный самостоятельно приобретать новые знания и применять их в изменяющихся условиях современной действительности.
В своей педагогической деятельности я столкнулась со следующей проблемой: как сформировать умение учащихся самостоятельно и творчески учиться. Одним из путей решения данной проблемы считаю, такую организацию учебной деятельности, в которой учащиеся играют главную роль. Свои знания учащиеся применяют умело и с пользой, если они усвоены в результате их самостоятельного труда. Следовательно, моя задача, как учителя, состоит в создании оптимальных условий для формирования самостоятельной активно мыслящей личности.
Создание и разрешение проблемных ситуаций на уроке позволяет мне включать учащихся в познавательный поиск, развивать их внимательность, учить выделять главное и существенное, сравнивать и анализировать, обобщать и делать выводы, уметь отстоять и доказать свою точку зрения, тем самым развивать их умственную самостоятельность.
1.3. Цели
Цель: развитие умственной самостоятельности учащихся посредством создания проблемных ситуаций на уроках математики.
1.4. Задачи опыта
Для достижения цели я выявила следующую последовательность действий и поставила следующие задачи:
провести психолого-педагогический анализ сущности проблемного обучения и его влияния на развитие умственной самостоятельности учащихся;
выявить особенности создания проблемных ситуаций и проектирования проблемных задач на уроках математики;
составить подборку проблемных заданий, способствующих развитию умственной самостоятельности учащихся;
2. Описание опыта
2.1. Ведущая идея опыта
«Идти не с предметом к детям, а с детьми - к предмету» (Н.И.Запрудский).
Ведущей идеей педагогического опыта является создание проблемных ситуаций с целью развития поисковой деятельности.
Знания без умений и навыков, как чемодан без ручки. Он есть, но зачем? Чтобы учащиеся овладели умениями и навыками необходимо, чтобы они для себя ответили на два вопроса: Зачем мне это надо? И как это делать? Ответив на первый вопрос, ко второму они подойдут осознано, осмысленно. Сами выдвинут ряд идей и гипотез, и предположений как это делать. Если с вопросом «Зачем?» учащихся не сталкивает жизненная ситуация, то моя задача выступить в роли координатора, а при ответе на вопрос «Как?» - в роли помощника. Таким образом, после мотивации возникнет цель, а цель побуждает умственную деятельность учащихся.
2.2. Описание опыта
Опыт опирается на теорию проблемно-деятельностного обучения. Концепция проблемно-деятельностного обучения была разработана в конце 80-х гг. XX в. коллективом педагогов под руководством А.В.Барабанщикова. Данная теория реализует два основополагающих принципа обучения: принцип проблемности и принцип деятельности в обучении. Сущность проблемно-деятельностной теории обучения заключается в том, что в процессе учебных занятий создаются специальные условия, в которых обучающийся, опираясь на приобретенные знания, самостоятельно обнаруживает и осмысливает учебную проблему, мысленно и практически действует в целях поиска и обоснования наиболее оптимальных вариантов ее решения.
Проблема – это осознанное затруднение человека в его деятельности.
Проблемная ситуация – это познавательная задача, которая характеризуется противоречием между имеющимися у учащихся знаниями и умениями, отношениями и предъявляемыми требованиями или новой информацией.
Умственная самостоятельность определяется как способность, которая состоит в том, что учащийся в совершенстве владеет общими умениями и навыками, необходимыми для познания реальной действительности, приобретения знаний, творческого их применения в сложившейся и новой ситуации.
Одна из важнейших составляющих психологического комфорта в математической деятельности – это ощущение радости от преодоления трудностей. Согласование необходимых требований и интересов учащегося возможно при личностно-ориентированном обучении.
По определению И.С. Якиманской, сущность личностно-ориентированного подхода заключается в том, что учащийся, его неповторимая индивидуальность, являются главной ценностью в образовательном процессе.
Таким образом, личностно-ориентированный подход на практике – это направленность образовательного процесса на учащегося, а не на предмет (Н.И. Запрудский).
Интересный урок - это урок сомнений, озарений и открытий, поэтому считаю, что при организации и проведении урока важное значение имеет реализация следующих принципов.
Принцип целеполагания и мотивации. Организовываю деятельность так, чтобы у учащихся выработался мотив и сформировались цели, (совместная формулировка целей, анализ домашнего задания).
Принцип доступности. Задания, которые я предлагаю, соответствуют возрасту учащихся и уровню их развития. На занятиях главный акцент я делаю на самостоятельную работу с индивидуальным темпом в сочетании с приемами взаимообучения и взаимопроверки, или формирую группы, которые обеспечивают взаимопомощь и продуктивное сотрудничество.
Принцип сознательности и активности отношу к одному из главных в обучении, так как он требует осмысленного усвоения знаний в процессе активной познавательной и практической деятельности. Предусматривает понимание учащимися цели и как действовать, чтобы достигнуть эту цель.
Принцип связи теории с практикой. Знать правила и формулы это одно. Если учащийся демонстрирует применение своих знаний в незнакомой ситуации, то это означает, что он приобрел умения и навыки. Также важно, чтобы учащиеся получили ответы на вопрос «А где мне это пригодится в жизни?».
Принцип творчества и успеха. Творческая деятельность учащегося позволяет развивать его индивидуальность. А его успехи помогают ему самоутвердиться.
Учебный процесс выстраиваю по принципу диалога, в котором учащиеся максимально могут проявить инициативу, высказать свою точку зрения, выслушать своих одноклассников и подискутировать по поводу предлагаемых идей.
Для того что бы учащиеся самостоятельно смогли увидеть и решить проблему необходимо поэтапно включать их в образовательный процесс. Поэтому в VI – VII классах использую метод проблемного изложения. Создаю проблемную ситуацию и помогаю наводящими вопросами раскрыть логическую цепочку решения. Учащиеся по ходу изложения задают вопросы и участвуют в обсуждении поставленной проблемы. Тем самым готовлю основу для перехода к следующему уровню проблемности, когда учащиеся сами формулируют проблему.
Процесс создания проблемной ситуации важный элемент в организации образовательного процесса.
«Сравните! Обобщите! Сделайте вывод!» – требования, побуждающие учащихся к познавательной деятельности. Для развития умственной самостоятельности стараюсь нацеливать учащихся на выделение существенной информации, обобщение фактов, признаков, явлений, классификацию предметов по их главным признакам, на практическое применение добытых знаний. На своих уроках математики я прослеживаю этот процесс.
Педагогические приемы, связанные с нацеленностью ребят на осмысление изучаемых явлений и формирование понятий, рассматриваю в процессе изучения всех тем математики. На учебных и факультативных занятиях применяю методические приемы:
1) Учащиеся приходят к противоречию, выполняя практическое задание.
VII класс. Тема «Неравенство треугольника». Учащиеся работают в группах. У каждой группы набор деревянных палочек следующей длины 6см; 7см; 8см; 10см; 2см; 3см; 4см; 5см; 11см.
Предлагаю составить треугольники: а) 6см; 7см; 8см; б) 10см; 6см; 7см; в) 3см; 4см; 5см; г) 4см; 5см; 11см; д) 2см; 3см; 5см. Учащиеся выполняют задание самостоятельно, и как бы они не пытались изменять углы и перекладывать палочку в последних двух заданиях, они сталкиваются с проблемой. «А вообще эти треугольники составить можно?» Почему первые три треугольника не вызвали затруднений? Учащиеся сравнивают и анализируют. «Какие длины должны иметь отрезки, чтобы можно было построить треугольник? Как они связаны?» Доказываем полученную теорему.
VII класс. Тема «Сумма внутренних углов треугольника». Учащиеся получают задание построить треугольник по трем углам. а)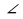 
А=90°, 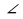B=60°, 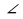С=30° б) 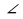А=90°, 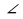B=60°, 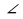С=45° в) 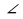А=70°, 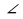B=30°, 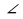С=50°. Первый треугольник построили, а вот со вторым и третьим проблема. Почему не получилось? Возникает интерес узнать новое. Первый рисунок может натолкнуть на продуктивную мысль.
2) Побуждаю учащихся проводить анализ, сравнивать, делать выводы, ставить конкретные вопросы (на обобщение, обоснования, конкретизацию, логику рассуждения).
VIII класс. Тема «Формула корней квадратного уравнения». Предлагаю учащимся решить несколько квадратных уравнений способом выделения квадрата двучлена: а)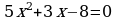
, б)
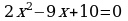, в)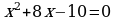
. С решением первого и второго учащиеся справились. Следует подчеркнуть, что решение этим способом идет четко по алгоритму. Это поможет в будущем навести учащихся на мысль решить квадратное уравнение способом выделения квадрата двучлена в общем виде. При решении третьего учащиеся столкнулись с проблемой. Примеры типа (x+a)2±b=0, где b не является квадратом целого числа, учащиеся ещё не решали. Способ выделения квадрата двучлена универсален, но требует каждый раз громоздких преобразований. В данной ситуации возникает познавательное затруднение, побуждает учащихся к сравнению, сопоставлению и к поискам нового способа решения.
VIII класс. Тема «Свойство медиан треугольника». Предлагаю учащимся: построить прямоугольный, тупоугольный и остроугольный треугольник; измерить длины сторон, найти середины каждой стороны и провести медианы. Выполняя построение, учащиеся приходят к первому выводу, что медиана пересекаются в одной точке. Далее прошу измерить и сравнить отрезки, на которые этой точкой делятся медианы. Учащиеся выдвигают гипотезу, что один из отрезков в два раза больше и уточняют именно какой. Далее формулируем свойство медиан и доказываем теорему. При доказательстве теоремы задаю лишь ориентир для учащихся (небольшие подсказки) и предлагаю им самим провести доказательство. Учащиеся могут применить свои знания.
VIII класс. Тема «Формулы сокращенного умножения». При выполнении ремонтных работ, дизайнер предложил выложить плитку по следующему рисунку.
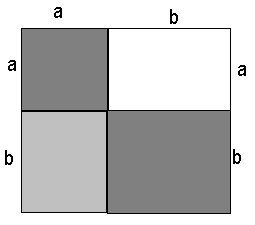
Сколько плиток нужно купить? Чтобы ответить на вопрос необходимо найти площадь. Учащиеся предложили два варианта решения этой задачи.
(a+b)2 и a2+ab+ab+b2=a2+2ab+b2. Каким бы способом мы эту площадь не искали ее величина не измениться пришли к выводу, что эти выражения можно приравнять. Далее учащиеся получают задания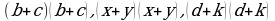 
. Решают, проводят сравнительный анализ решения, ищут закономерность, делают вывод.
3) Предлагаю практико-ориентированные задачи, например: Два мальчика пришли в пиццерию. Что выгоднее им купить: две пиццы по 2 руб. диаметром 20 см или одну пиццу за 4 руб. диаметром 40 см?
4) Предлагаю различные точки зрения на один и тот же вопрос.
VIII класс. Тема «Решение квадратных уравнений». Учащиеся уже умеют решать квадрантные уравнения способом выделения полного квадрат, применяя формулы корней и по теореме Виета. Но теорема Виета применяется лишь для приведенных квадратных уравнений. С целью развития навыков устного счета знакомимся еще с одним способом решения. Метод «переброски»
VII класс. Тема «Сумма внутренних углов треугольника». На уроке провожу несколько доказательств теоремы и предлагаю учащимся найти свое. Учащиеся предложили разрезать треугольник и сложить развернутый угол, тем самым продемонстрировали творческий подход.
5) Предлагаю составить задачи самостоятельно. Данный прием развивает мышление, повышает интерес.
6) Предлагаю домашние задание, которое создаст проблемную ситуацию.
При изучении темы «Площадь параллелограмма», задаются дополнительно задачи на нахождение площади прямоугольного треугольника и остроугольного треугольника. С прямоугольным треугольником многие учащиеся справились, достроив его до прямоугольника. А вот с остроугольным треугольником возникла проблема. На уроке тема «Площадь треугольника» эти задачи выступают в роли проблемных заданий.
7) Предлагаю решить проблемные задачи. Опираясь на типологию задач, предложенную психологом В. А. Крутецким.
8) Использую игровые приемы.
V класс. Тема «Признаки делимости на 3 и на 9». Два-три учащихся выступают в роли знатоков. Они самостоятельно разобрали данные признаки делимости и подготовились к игре. Учащийся на доске пишет число, а один из знатоков дописывая цифру, утверждает, что полученное число делится на 3. Класс, воспользовавшись калькулятором проверяет. Числа могли оказаться достаточно большими. В итоге у класса возник интерес, как знатоки это делают. Знатоки с гордостью делятся своими знаниями.
Анализ проблемной ситуации - это первый шаг самостоятельной умственной деятельности учащихся. Осмысление ситуации приводит учащихся к пониманию того, что именно является причиной возникшего интеллектуального затруднения, к возникновению в сознании вопроса: как решить поставленную задачу?
Думать, значит уметь задавать себе вопросы и отвечать на них. У учащегося возникают вопросы: Что нужно найти? Чего не хватает для достижения цели?
Учебная проблема считается поставленной в том случае, если созданы условия для самостоятельного решения ее учащимися. Логика решения учебной проблемы, и схемы ее решения указывают на необходимость составления плана решения. Составление плана решения зависит от умения учащегося предвидеть следующие шаги. В итоге такого мысленного «забегания» вперед возникает идея решения, предположение. Дальнейший ход мысли требует проверки, обоснования правильности выдвинутого предположения. Умение учащегося находить в учебном материале нужные факты и приемы для доказательства и практической проверке правильности предположения, гипотезы – одно из условий успешного решения учебных проблем. В организации поиска решения я задаю вопросы, направляющие мысль учащихся на анализ необходимых фактов, обращаю их внимание на неправильность или несостоятельность тех или иных предположений, тем самым направляю к правильным предположениям, обоснованию гипотез и их подтверждению фактами.
Выдвижение первичных предложений о пути решения проблемы, процесс поиска решения и достижение успеха, дает учащемуся осознание того, что это сделал «Я – сам».
Очень важно организовать решение поставленной проблемы в ходе поисковой деятельности. Умственная деятельность учащегося должна быть направлена на разрешение ситуации, тогда как обучение будет являться результатом.
2.3. Результативность и эффективность опыта
Результативность и эффективность опыта подтверждается сформированностью умственной самостоятельности учащихся, которая определена следующими критериями:
умение разделять материал (источник добывания знаний) на логически целостные части;
умение составлять план;
умение переходить от одной составной части к другой;
умение аргументированно сопоставлять явления по существенным признакам; выделять главные признаки и особенности явлений, процессов и т.п.;
умение делать выводы и заключения;
умение переносить приобретенные знания в новые условия.
3. Заключение
Анализируя свой опыт, результаты анкетирования, приходим к выводу, что создание проблемных ситуаций на уроке не только актуально, но и необходимо, так как способствует развитию самостоятельности, нестандартности мышления учащихся, позволяет сформировать стойкую учебную мотивацию, использовать полученные навыки решения проблемных ситуаций для решения практических задач.
Перспектива дальнейшего совершенствования заключается в возможности решения проблемных ситуаций с применением элементов исследовательской деятельности с целью формирования учебно-познавательных компетенций.
Список литературы
Запрудский, Н.И. Педагогический опыт: обобщение и формы представления: пособие для учителя / Н.И.Запрудский. – Минск : Сэр-Вит, 2014. – 256 с.
Крутецкий, В.А. Психология: Учебник для учащихся пед. училищ./В.А.Крутецкий — М.: Просвещение, 1980.—352 с, ил.
Перевознюк, Е.С. Уроки математики в рамках концепции личностно-ориентированного обучения /Е.С. Переворзнюк// Математика в школе. – 2003. -№ 5
