Методика проведения занятия по теме:" Многочлен и действия с ним."

МОУ ВВСШ г.Чусовой.

Урок повторения по теме

«Многочлены и действия с ними»

7 класс

Учитель: Гончаров А.В, учитель

математики первой

квалификационной категории

Чусовой 2011

Урок повторения и обобщения знаний по теме

«Многочлены и действия с ними»

Цели:

1) повторение знаний по теме «Многочлены и действия с ними»; закрепление умений и навыков выполнения действий с многочленами; отработка вычислительных навыков при упрощении выражений и решении уравнений;

2) формирование навыков самостоятельной работы, коммуникативных умений, развитие навыков умственного труда, быстроты мышления, творческого начала в умственной деятельности; формирование умений осуществлять самоконтроль и взаимоконтроль;

3) формирование культуры общения, сознательной дисциплины, воспитание чувства взаимопомощи.

Пояснительная записка к технологии, применяемой на уроке:

На уроке использована технология групповой работы, приемы интерактивного обучения – обучение в общении. Особенность этого метода – процесс обучения происходит в совместной деятельности. Главная идея – «все обучают каждого, каждый обучает всех». Работая в небольших группах, ученики начнут отвечать за успехи каждого, и научатся помогать друг другу. Практика показывает, что вместе учится не только легче и интереснее, но и эффективнее. Здесь уделяется внимание «групповым целям», успеху всей группы, который может быть достигнут только в результате самостоятельной работы каждого члена группы в постоянном сотрудничестве с другими членами этой же группы при работе над тем или иным вопросом.

Идея сводится к трем основным принципам:

1. «Награду» команда получает одну на всех в виде общей отметки (или другого поощрения). Для этого необходимо выполнить общее задание.

2. Индивидуальная ответственность каждого ученика означает, что успех или неуспех всей группы зависит от удач или неудач каждого его члена. Это стимулирует всех членов команды следить за успехами друг друга.

3. Равные возможности для достижения успеха означают, что каждый приносит баллы своей группе. Что позволит любому (слабому, среднему) ученику чувствовать себя полноправным членом команды.

Оборудование:

1. Контрольные карты для каждой группы.

2. Карточки-задания для каждой группы.

3. Карточки с заданиями для каждой группы в туре «Поле чудес».

4. Тесты (с дифференцированными заданиями) для каждого ученика.

5. Карточки с ответами к тесту для каждого ученика.

6. Таблица с ответами и соответствующими буквами к ним для тура «Поле чудес» (на доске).

Ход урока.

1. Организационный момент.

Учащиеся делятся на группы по 4-6 человек. Формирующиеся группы являются разноуровневыми, т.е. в каждой группе есть ребята разного уровня математической подготовки.

Задача каждой группы за урок заработать как можно больше баллов. Успех группы зависит от успешности работы каждого, в постоянном взаимодействии с другими членами этой же группы.

Группа получает одну бальную оценку на всех. Ответственность каждого ученика стимулирует всех членов группы следить за успехами друг друга и всей командой приходить на помощь своему товарищу.

Команды не соревнуются друг с другом, а работают лишь с целью заработать как можно выше балл.

В каждом туре руководитель проставляет напротив фамилии каждого члена группы столько баллов, сколько им решено правильно заданий.

2. Устная работа.

1. Дать определение многочлена.

2. Какой многочлен называется многочленом стандартного вида?

3. Какие слагаемые называются подобными?

4. Что значит «привести подобные слагаемые»?

5. Как умножить одночлен на многочлен?

6. Как умножит многочлен на многочлен?

7. Упростить выражение (карты), (а+n) + (b - n); (b + n)-(n - a); (a -n) + (b +n).

8. Продолжить равенство (на доске):

(x² + 2)(x² + x + 1) =

(x² + 2x + 1)(x - 4)=

9. Назвать общий множитель (карты), 4а² – 4вс; - 8у³ – 24у; ас + с + с².

10. Что значит многочлен разложить на множители?

11. Какие способы разложения многочлена на множители вы знаете?

12. Назвать способ разложения на множители (на доске):

m² + 4m + 4; m² - 64n²; 6mx – 2m + 9x – 3; 2m⁶ - 4m³ + 6m

13. Вычислить рационально

53²- 43² = 960 34² + 2·34·36 + 36² = 4900 167² - 167·67= 167·100=16700

14. Доказать (на доске):

(3¹⁷ + 3 ¹⁵ ) : 30, 3¹⁵(3² + 1) : 30, (3¹⁵ ∙ 10) : 30

Заполнение контрольных карт

Контрольная карта группы №___

№ п/п

Тип работы Ф.И. ученика

Практическая работа

Поле чудес

Тест

Д.з.

Итог

№1

№2

№3

№4

1.

2.

3.

4.

5.

Общее количество баллов, набранное группой за урок __________

3. Работа в группах.

Учитель раздает группам задания. За определенное время группа должна решить задания на карточках. По мере решения одной карточки, выдается другая. Учитель (или помощник) проверяет правильность решения и группы заполняют контрольную карту.

Задание №1

Решить уравнение.

1. ;

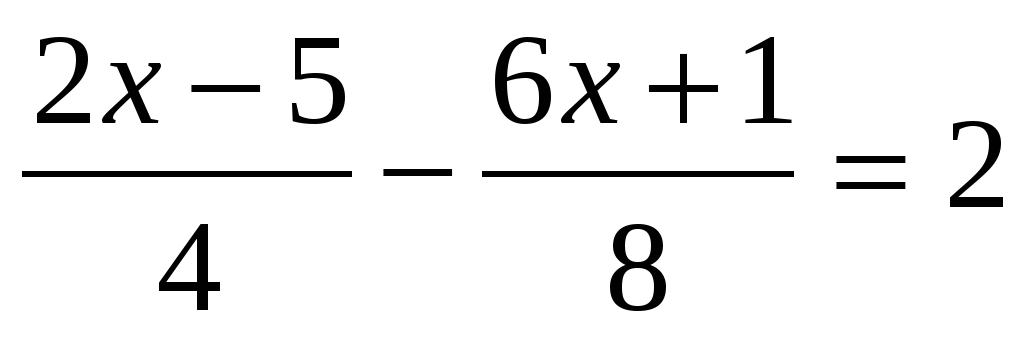2. 7 (x+1) – 2 (x- 4)= x - 2;

3. 3 + x(5-x)= (2 - x)(x+3);

4. 12x² – x=0;

5. t² - 625=0;

6. 16y² - 36=0.

Задание №2

Вынести общий множитель.

1. 4a² - 8a³+12a⁴;

2. – 15a³b²c -10a²b²c² - 5ab²c³;

3. – 3x⁶+12x¹²;

4. 5x(b-c)-(c-d);

5. 6ax+6ay;

6. (x-5)(2y-3)+(x- 5)(4y+1);

7. a⁵-a⁴-a²;

8. (x-y)² – a(x-y).

Задание №3

Умножить многочлен на многочлен.

1. (x-7)(x+3);

2. (4m²+6)(4m-6);

3. (2x²- x)(8x² - 2x);

4. (a-4b)(a²+3ab - 6b²);

5. - 3c³(6-4c)(2c²-9c).

Задание №4

Разложить многочлен на множители.

1. x³-3x²-x;

2. 6a²-2ab-3ac+dc

3. 49x²y² - 400

4. a(b-c)+3(с-b)

5. 7c² - c - c³+7

6. 9a² - 30a+25

7. 27+b⁹

8. (p²-6) - q(p²-6)².

(Ответы к заданиям у учителя или помощника).

4. Тур «Поле чудес»

Задача каждой группы – разгадать высказывание, буквы из которых оно состоит можно узнать, решив соответствующее задание и найдя ответ в таблице. Узнав буквы, их нужно расположить в том порядке, в котором пронумерованы задания.

Если группа угадывает высказывание правильно, то она зарабатывает 20 баллов (по количеству букв в высказывании). А каждый член группы в контрольной карте напротив своей фамилии ставит столько баллов, сколько примеров (сколько букв отгадал) он решил.

у	м	ш	т	н	о	а	р	и	с	д	Е
-6a	3a3	-8ax	-25x	12n	3m4	-7b3	-x2-12-31	-11c	-6ac	-15y	3x2
л	в	ь	ч	я	х	п	г	й	к	ж
-29m	-23b	-10x2	5y2-xy	11x3	-11a2	-27b	-3x2-36x	-4x3100xy	-a3	-24xy

1 группа – Умному и слова довольно

№1 3а (8в - 5) – 6(4ав – 1,5а) 5) а(8а2 – 4а) – а2(5а - 4) 11) 6(ас – в ) – (6ас + 17в) 18) 4х (2х + 3) – 6х(3х – 2 )	№2 а2 (4в - а) – 4а(ав – а2) 6) (6а – 8ав) + 4а(2в - 3) 9) - 4m(5m2 + 6 ) – 5(m – 4m3) 14) 6m2 (m2 – 2a) – m(3m3 – 12am )
№3 - (3m + 6n) + 3(m + 6n) 8) 4c(- 3а + b) – 2c(2b – 3a) 13) 3x(2 – 3y ) – 6(xy + x) 19) 6n(3 - 5b ) – 6(n – 5bn )	№4 5) 2y(x – y ) + y(7y – 3x) 11) - 9x(x + 2) + 2x(6x + 9) 15) 3b(2 – 5b2 ) – 2(3b – 4b3) 19) 6х (-5/6 + 3x) – 3х(7 + 6x )
№5 8(ab - c) – (8аb + 3c) 12) 3b(2 – 5b2) – 2(3b – 4b3) 16) 2m3(6b - m) –4m (3bm2 – 1,25m3) 17) - (4a + 5m) + 8(0,5 – 3m )

2 группа – Повторенье – мать ученья

№1 3x(x – 7 ) – x(4 + 3x) 10) 3x(7x – 2 ) – 2x(9x – 3 ) 13) -5x (x + 4) – x(5 – 5x ) 18) 6n (3 - 5b) – 6(n – 5bn )	№2 1) - (3a2 + 6b) + 3(a2 – 7b) 7) – 9x(x + 2) + 2x(6x + 9) 15) 3a(8b – 5 ) –6 (4аb + 1,5a) 19) -5х(3х + 1) + 5х(х + 1 )
№3 4m (2n – 3m3) – 3m(-5m3 +8/3n) 9) 4x(2x + 3) – 6x(3x – 2 ) 14) 0,25x(4x +100 ) –x (11x + 25) 17) 0,5х(4 – 16x) – х(-5х + 2 )	№4 - (8ac + 3b) + 4(2аc – 5b) 8) - (3m + 6n) + 3(m + 6n) 12) 3b(2 – 5b2 ) – 2(3b – 4b3) 20) х(3х2 – 4 ) + 4(х + 2 x3)
№5 6m3(4m2 –m) – 4m2(6m3 – 2,25m2) 6) (3x +9) + (- x2 – 15x – 40 ) 11) a(8а2 – 4a) – a2(5а – 4 ) 16) 2y (х – y ) + y(7y - 3х )

3 группа – Для ученья нет старости

№1 2) - 4m(5m2 + 6 ) – 5(m – 4m3) 6) 3x(7x – 2 ) – 2x(9x – 3 ) 12) 3x(x – 7 ) – x(4 + 3x) 18) -5a(4b + 6c) + 4a(6c +5b )	№2 3) х(3х2 – 4 ) + 4(х + 2 x3) 9) x2(3x 2 + 6x ) – x3(3x2 – 5 ) 14) -5x (x + 4) – x(5 – 5x ) 20) -2c(3 -5a2 ) + 5(-c – 2a2c )
№3 1) 3x(2 – 3y) – 6(xy +x) 7) - (3m + 6n) + 3(m + 6n) 10) 6n (3 - 5b) – 6(n – 5bn ) 16) (3x + 9) + (- x2 – 15x - 40)	№4 4) 6m3(4m2 –m) – 4m2(6m3 – 2,25m2) 10) 4m (2n – 3m3) – 3m(-5m3 +8/3n) 15) - (8ac + 3b) + 4(2аc – 5b) 20) m(2a + m3) – 2 (am – m4 )
№5 4) 3a(8b – 5 ) –6 (4аb + 1,5a) 8) -3(c2 + 5c ) + c(3c + 4 ) 13) 4c(- 3а + b) – 2c(2b – 3a) 17) 6m3(4m2–m) – 4m2(6m3 – 2,25m2)

4 группа – Век живи – век учись

№1 2) 3x(7x – 2 ) – 2x(9x – 3 ) 7) 8(ab - c) – (8аb + 3c) 12) 2y(x – y ) + y(7y - 3x)	№2 3) 6a(5a – a2) + 4a(1,25a2 – 7,5) 8) 4(3am + 0,25b ) – 8(1,5am + 3b) 11) 3a(8b – 5 ) –6 (4аb + 1,5a)
№3 1) 6(ас – в ) – (6ас + 17в) 5) -3(c2 + 5c ) + c(3c + 4 ) 10) 3a (a2 +2a) – 4a(a2 +1,5a)	№4 4) 2x(14x2 -2y) – 4x(5y + 7x2) 9) – 9x(x + 2) + 2x(6x + 9) 14) 4c(- 3а + b) – 2c(2b – 3a)
№5 6) - (8ac + 3b) + 4(2аc – 5b) 13) – 2c(3 – 5a2) + 5(- c – 2a2c) 15) 4x(2x + 3) – 6x(3x – 2 )

5 группа – Учи других – сам поймешь

№1 3) -3(c2 + 5c ) + c(3c + 4 ) 8) 8(ab - c) – (8аb + 3c) 12) 3b(2 – 5b2 ) – 2(3b – 4b3) 16) 10x(5x2 – 7y) – 6x(5y + 9x2)	№2 2) 2y(x – y ) + y(7y - 3x) 5) (3x + 9) + (- x2 – 15x - 40) 11) -5a(4b + 6c) + 4a(6c +5b ) 17) а2 (4в - а) – 4а(ав – а2)
№3 1) 3a(8b – 5 ) –6 (4аb - 1,5a) 9) 2a(a2 – 4a) – a2 (2a + 3) 14) - (3a2 + 6b) + 3(a2 – 7b) 19) -y(2a +4y) – 2y(3a – 2y)	№4 4) 3x(2 – 3y) – 6(xy - x) 7) 3x(x - 8) – 6 (x2 +2x) 13) a(8а2 – 4a) – a2(5а – 4 ) 18) 3x(7x – 2 ) – 2x(9x – 3 )
№5 6) (6а – 8ав) + 4а(2в - 3) 10) – 2c(3 – 5a2) + 5(- c – 2a2c) 15) 4m (2n–3m3) – 3m(-5m3 +8/3n) 20) 4x(2x + 3) – 6x(3x – 2 )

Таблицы к ответам тура 4

№ задания	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
буква

Заполнение контрольных карт.

5. Тестирование.

Каждый член команды получает индивидуальное задание в виде теста. Затем члены команды проверяют друг у друга результаты тестирования. Каждый член группы получает то количество баллов, сколько заданий решено правильно и вносится в контрольную карту (напротив фамилии каждого ученика).

Варианты тестов:

Вариант 1 1. Решить уравнение 3 – 4(2х - 5) = 2 – 6х а) 2/21 б) 8,5 в) 10,5 г) 12 2. Назовите общий множитель 3х5у2 + 15х4у3 + 12х3у4 а) 3х5у4 б) 60х3у2 в) 3х3у2 г) х3у2 3. Упростите выражение (2 + х)(3х – 5 ) – 3х(3 + х2) а) -3х3 + 3х2 -8х – 10 б) -3х6 – 10 в) 3х3 + 3х2 + 3х – 10 г) 3х3 + 3х2 + 15х – 10 4. При выполнении действий заполните пропуски (2 + а – а3 + а5)(а - 1) = 2а + а2….+ а6 – 2….+ а3 – а5	Вариант 2 1. Решить уравнение 3х(х - 7) – х(4 +3х) = 5 а) -5 б) -1/5 в) 1/5 г) 5 2. Назовите общий множитель 20х4 - 25х2у2 - 10х3 а) х2 б) 5х2у2 в) 5х2 г) 5х4у2 3. Упростите выражение х2(2х - 3) + (2х + 5)(2х – 5 ) а) 2х3 - х2 -20х – 25 б) 2х3 + х2 – 25 в) 2х3 - х2 – 25 г) 3х7 – 25 4. При выполнении действий заполните пропуски (5b2 - 1)(b3 – 5b2 + b) = 5b5…..+ 5b3 – b3… - b
Вариант 3 1. Решить уравнение а) -4/49 б) -12,25 в) -11,5 г) 12,25 2. Назовите общий множитель 6m2n2 +9m2n – 12mn2 а) mn б) 3mn в) 3 m2n2 г) m2n2 3. Упростите выражение (х +6)(х +6 ) – (3 – х)(5 - х) а) 12x + 9 б) 2x2 +2x + 9 в) 2x + 9 г) 18x + 9 4. При выполнении действий заполните пропуски (x2 – 10x)(-x3 - 6) = -x5 – 6x2…….	Вариант 4 1. Решить уравнение 14х2 - (2х - 3) (4 +7х) = 14 а) 2/13 б) 6,5 в) -13/28 г) -2/29 2. Назовите общий множитель 6a2b2 – 8a2b + 12ab2 а) ab б) a2b2 в) 2ab г) 24ab 3. Упростите выражение (х - 6)(х + 5) – x2(х2 – 5x +1 ) а) - х4 + 5x3 – x – 30 б) - х4 - 5x3 – x – 30 в) - х4 + 2x2 +5x3 – x – 30 4. При выполнении действий заполните пропуски (- 3n2 + 2n)(3n3 + 2n2) = -9n5……+6n4
Вариант 5 1. Решить уравнение (8х + 10)(3 - х) = (11 -2х)(4x +5) - 5 а) -1/2 б) 1 в) - 1 г) 1/2 2. Назовите общий множитель 8х3y3 + 88х2у3 - 16х3y4 а) 8х3y4 б) 8х2у3 в) 88х2y3 г) х3у4 3. Упростите выражение - 5c2(6 – 4c)(2c2 +7c) а) -90c2 б) 210c3 + 40c5 – 80c4 в) - 210c3 + 40c5 + 80c4 4. При выполнении действий заполните пропуски (-3n2 + 2n + 1)( 3n2 + 2n - 1) = -9n4 – 6n3…..+ 6n3 + 4n2 – 2n + 3n2…. -1

Ответы к тестам

Варианты
1	2	3	4	5
в в а –а4 -а	б в б – 25b4 + 5b2	г б г + 10х4 +60х	а в а - 6n4 + 4n3	в б в +3n2 +2n

6. Творческое домашнее задание.

1. Составить тематический словарь по теме «Многочлены и одночлены».

2. Составить систему карточек-заданий по теме «Многочлены и действия с ними».

3. Составить кроссворд по теме «Многочлены и одночлены» (15-20 слов).

4. Написать сочинение-интервью «Интервью с многочленом (или одночленом)» или сказку на эту же тему.

За качественное выполнение творческого домашнего задания каждый член группы получает от 1 до 5 баллов (заполняются контрольные карты).

7. Подведение итогов.

Руководитель каждой группы подсчитывает количество набранных баллов каждым членом команды и заносит в соответствующую строку контрольной карты напротив его фамилии. Результаты всех членов суммируется и засчитывается на счет всей команды.