Конспект по математике на тему: Перпендикуляр түзулер.

Тақырыбы:

Перпендикуляр түзулер.

Күні,айы:

Мұғалімнің аты-жөні: Халмурадова Махбуба

Сабаққа қатысқан оқушылар саны:

Сабаққа қатыспаған оқушылар саны:

Оқу бағдарламасына сәйкес оқу мақсаты

7.1.2.8

Перпендикуляр, көлбеу және көлбеудің проекциясы ұғымдарын меңгеру;

7.1.2.9

нүктеден түзуге түсірілген перпендикулярдың біреу ғана болуы туралы теореманы дәлелдеу және қолдану;

7.1.2.10

перпендикуляр түзулердің қасиеттерін білу және қолдану;

Сабақ мақсаты

Барлық оқушылар:

Перпендикуляр түзулерді анықтайды, перпендикуляр белгісін біледі және оны дәлелдейді; нүктеден түзуге түсірілген перпендикуляр, перпендикулярдың табаны, нүктеден түзуге дейінгі қшықтық, ұғымдарын анықтайды.

Оқушылардың басым бөлігі:

Өткен тақырыппен байланыстырады;-Оқушының жеке ой- пікірінің құндылығы артады.

Кейбір оқушылар:

Оқушылар жаңа тақырып жайлы малғұматтар алады ол туралы оқып үйренеді

Сабақтың барысы

Сабақтың кезеңдері

Жоспарланған жұмыс

Ресурстар

Сабақтың басы(2-5 минут)

(МК) Ал, балалар, бүгінгі көңіл күйіміз жақсы екен, ендіше үй тапсырмасын тексеремін. Үй жұмысы қандай?

Екі үшбұрыштың үш қабырғасы және үш бұрышы тең, олар тең үшбұрыштар ма?

Барлық қабырғасы тең үшбұрыш тең бүйірлі үшбұрыш па?

Екі тікбұрышты үшбұрыштың сүйір бұрыштары тең, олар тең
үшбұрыштар ма?

Бір катеті және бір бұрышы (сүйір бұрышы болмауы да мүмкін) тең тікбұрышты үшбұрыштар, тең үшбұрыштар ма?

Катет гипотенузадан үлкен болуы мүмкін бе?

Екі тікбұрышты үшбұрыш тең егер олардың сәйкес екі катеттері тең болса. Осы берілген теоремаға кері теорема жазыңыз.

Сабақтың ортасы (6-40 минут)

(МК,Ұ)

Есепт

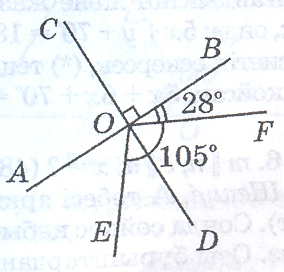
ер шығару

1. а және b түзулерінің қиылысуында пайда болған бұрыштардың үшеуі өзара тең. а ┴ b екенін дәлелдендер.

Шешуі. Қиылысқан а және b түзулері берілсін.Олар қиылысқанда пайда болған бұрыштардың үшеуін 1; 2 және 3 деп белгілейік. Шарт бойынша

2. АВ және СD перпендикуляр түзулері О нүктесінде қиылысады. ОЕ және ОF сәулелері ОD сәулесімен бір жарты жазықтықта жатады және

Шешуі. Есептің шартына сәйкес сурет саламыз ВОЕ және АОЕ – сыбайлас бұрыштар. Сондықтан

Жауабы: 62°, 43°.

Оқулық

Аудидиск:

1.4.1; 1.4.4;

Жұмыс дәптері

Сабақтың соңы( 41-45мин)

Дәптермен жұмыс.

1 Өздік жұмыс

№1

Екі доғал бұрыштың ортақ қабырғасы бар, ал қалған екі қабырғасы өзара перпендикуляр.

Егер доғал бұрыштар тең екендігі белгілі болса, доғал бұрыштың шамасын тап.

Жауабы:

∠АОВ = ∠АОС

ВО⟘ ОС,

∠ВОС = 90

2∠АОВ = 360 – 90 =270

∠АОВ = 135

№2

Жазыңқы бұршытың төбесінен екі сәуле жүргізілген, олар оны ұш тең бөлікке бөледі. Ортаңғы бұрыштың биссектрисасы жазыңқы бұрыштың қабырғаларына перпендикуляр екендігін дәлелдеу керек.

Жауабы:

∠АОВ = ∠ВОС = ∠СОD=60, ОК – биссектриса,

∠СОК = ∠ВОК = 30

∠DOK = 90

∠АОК= 90

Сабақты қорытындылау

Қосымша ақпарат

Қорытындылау

Төмендегі бөлікті сабағыңыз туралы өз ойыңызды жазуға қолданыңыз.Өз сабағыңыз бойынша сол жақ бағандағы сұрақтарға жауап беріңіз.

1.Сабақ барысында өзгертулер енгіздіңіз бе?

2.Жүргізген жұмыс түрлері қаншалықты тиімді болды?

Қорытынды бағалау

Ең жақсы өткен екі нәрсе?

1.

2.

Қандай екі нәрсе сабақты жақсартар еді?

1.

2.