Итоговая контрольная работа по геометрии за 8 класс

Итоговая контрольная работа по геометрии

8 класс

1 вариант

1. Найдите площадь равнобедренного треугольника со сторонами 10см, 10см и 12 см.

2. В параллелограмме две стороны 12 и 16 см, а один из углов 150°. Найдите площадь параллелограмма.

3. Длина солнечной тени от дерева равна 24 м. Вертикальный шест высотой 1 м 50 см тот же момент отбрасывает тень длиной 1 м 60 см. Вычислите высоту дерева.

4. В треугольнике АВС прямая MN, параллельная стороне АС, делит сторону ВС на отрезки BN=15 см и NC=5 см, а сторону АВ на ВМ и АМ. Найдите длину отрезка MN, если АС=15 см.

5. В окружности проведены две хорды АВ и СD, пересекающиеся в точке К так, что КС=6 см, АК=8 см, ВК+DК=21 см. Найдите длины ВК и DК.

6. В прямоугольном треугольнике АВС 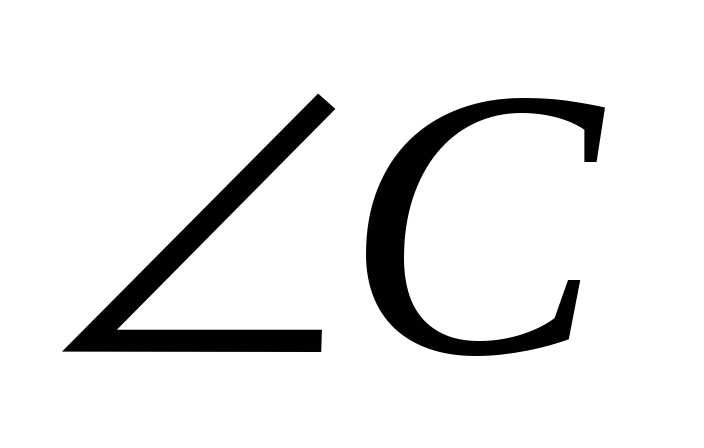=90°, АС=8 см, 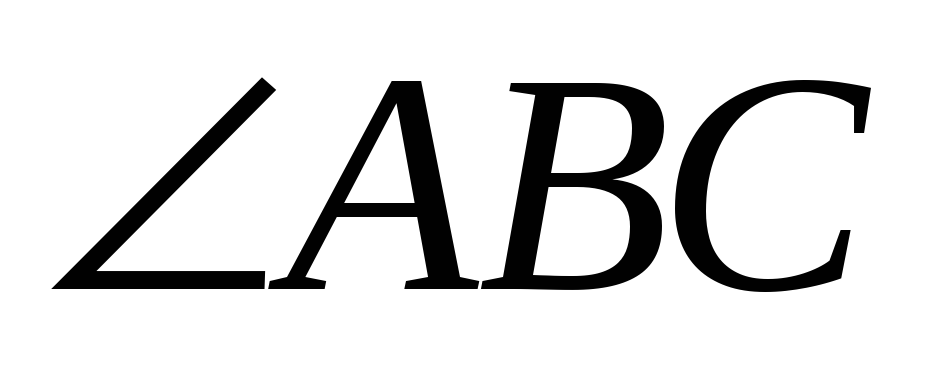=45°. Найдите:

а) АВ; б) высоту СD, проведенную к гипотенузе.

2 вариант

1. В равнобедренном треугольнике боковая сторона равна 13 см, а высота, проведенная к основанию, 5 см. Найдите площадь этого треугольника.

2. .Найдите длину солнечной тени от здания высотой 11,7 м, если солнечная тень от человека ростом 1,8 м равна 2 м.

3. В прямоугольной трапеции АВСД боковая сторона равна АВ=10 см, большее основание АД= 18 см, 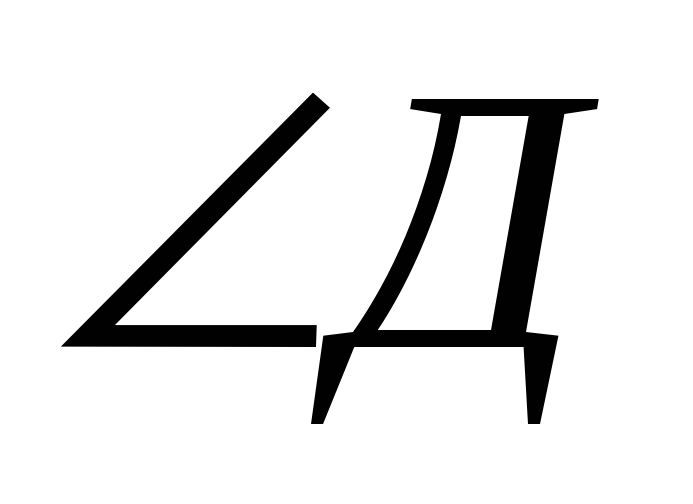=45°. Найдите площадь трапеции.

4. В окружности проведены две хорды АВ и СD, пересекающиеся в точке М так, что МВ=10см, АМ=12 см, DС=23 см. Найдите длины СМ и DМ.

5. В треугольнике АВС со сторонами АС=12 см и АВ=18 см проведена прямая MN, параллельная АС, MN=9 см. Найдите ВМ.

6. В прямоугольном треугольнике АВС 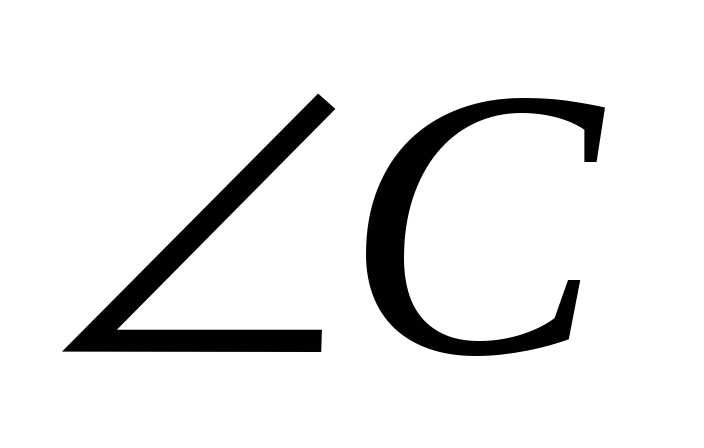=90°, АС=8 см, 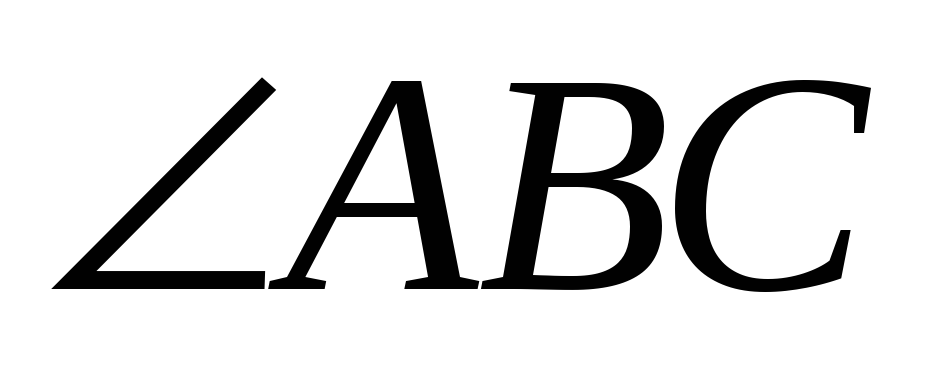=45° . Найдите:

а) АВ; б) высоту СD, проведенную к гипотенузе.