
Множества и операции над ними.
Исследовательская работа

Введение.
Знания – это всё то, без чего нельзя жить в
нашем мире. Без знаний человек не может чувствовать себя полезным членом современного общества и принимать правильные решения в повседневной жизни. Именно математика, как никакой другой учебный предмет, развивает человеческие качества. Об этом говорили многие известные ученые прошлого.
Математика – это оружие для размышления.
Р. Фейнман
У человека , знающего математику , на один орган чувств больше. Ч. Дарвин
Математику уже затем стоит изучать , что она ум в порядок приводит. М.В. Ломоносов

Моя работа представленная Вашему вниманию, рассматривает вопросы, связанные с самой интересной в мире теорией множества.
Актуальность моей работы очевидна.
Многие из нас даже не задумываются над тем, что множество имеет большое значение в нашей жизни. Любая область человеческой деятельности связана не только с одним предметом, объектом, а с целой совокупностью.
Например: медицина изучает не одну отдельно взятую болезнь, а все болезни; зоология изучает не отдельно взятое животное, а совокупность всех животных. Математика, как и другая область человеческих знаний, изучает те или иные объекты не каждый в отдельности, а в их связи между собой.

Цель моей работы:
Применить принципы теории множеств для расширения собственного мировоззрения.
Задачи:
1. Изучить понятие множества и способы операций над множествами.
2. Исследовать связи над операциями над множествами и обычными операциями с числами
3. Научится решать и составлять задачи на тему «Множества».

Объекты исследования:
1. Множества и круги Эйлера.
2. Задачи на тему «Множества».
Методы исследования:
1. Изучение литературы и работа с Интернетом.
2. Сравнительный анализ.
(связи над операциями над множествами и обычными операциями с числами).
3. Практическое исследование.
(Решение задач).

Гипотеза:
Теория множеств– это своего рода основа математического языка, без него невозможно заниматься математикой. Любая область человеческой деятельности связана не только с одним предметом, объектом, а с целой совокупностью объектов.
Практическая значимость:
Представленный в работе материал может использоваться на занятиях математического кружка в 5–6-х классах.

Что такое множество?
По словам Георга Кантора, «множество – есть многое, мыслимое нами как единое целое».
Множеством может именоваться некоторая совокупность элементов, объединенных по какому-либо признаку. Слово «множество» указывает, что должно быть много элементов. Хотя это не так. Элементов может быть 2, например множество спутников Марса; 1, например
естественных спутников Земли
и даже нисколько, так называемое
пустое множество.

Пустое множество.
Пустое множество – это множество, которое не содержит элементов.
Обозначается: Ø
Например: множество квадратных колёс или прямых кривых. В пустом множестве количество элементов выражается числом 0, следовательно, оно конечное.
При помощи пустого множества можно создать ещё очень много различных множеств, не смотря на то, что это множество «пустое».
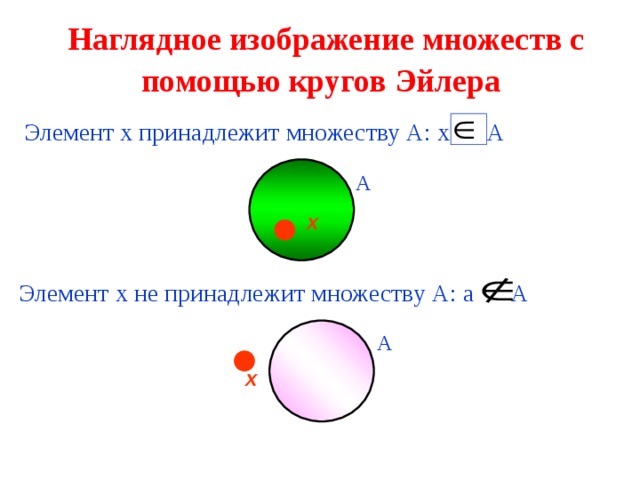
Наглядное изображение множеств с помощью кругов Эйлера
Элемент х принадлежит множеству А: х А
А
х
Элемент х не принадлежит множеству А: а А
А
х

Конечные и бесконечные множества:
Множество, количество элементов которого, выражается некоторым числом, называется конечным .
Примеры: множество страниц в книге, множество камней на морском берегу.
Но если множество не является конечным, то есть, у него нет точного количества элементов, это множество называется бесконечным .
Например: множество натуральных чисел N .
В бесконечных множествах элементы соединяют в группы по характеристическим свойствам.
{ х │ 2 х 7 }
Множество всех х таких, что 2
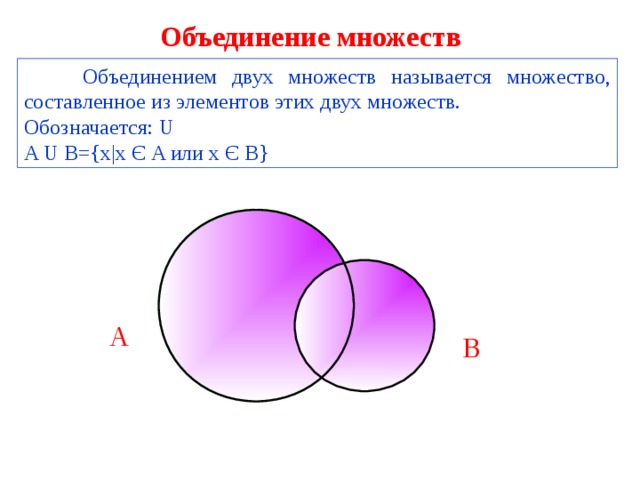
Объединение множеств
Объединением двух множеств называется множество, составленное из элементов этих двух множеств.
Обозначается: U
A U B ={х|х Є A или х Є B }
А
В

Моя задача.
В фотоальбоме много фотографий. На 21 фотографии моя сестра. На 30 – я. На 14 – мы с сестрой фотографировались вместе. А на 6 фотографиях нет ни одного человека, там изображена природа. Сколько фотографий в фотоальбоме?
Решение:
Пусть A – множество фотографий с моей сестрой. По условию A = { 21 } .
Пусть B – множество фотографий со мной. Количество элементов B = { 30 } .
Пусть C – множество фотографий меня и сестры. По условию C = { 14 } .
Пусть D – множество фотографий с природой. По условию D = { 6 } .
Пусть K – множество всех фотографий.
A + B-C+D= 21+30-14+6= K K = { 48 } .
Ответ:48 фотографий в фотоальбоме.
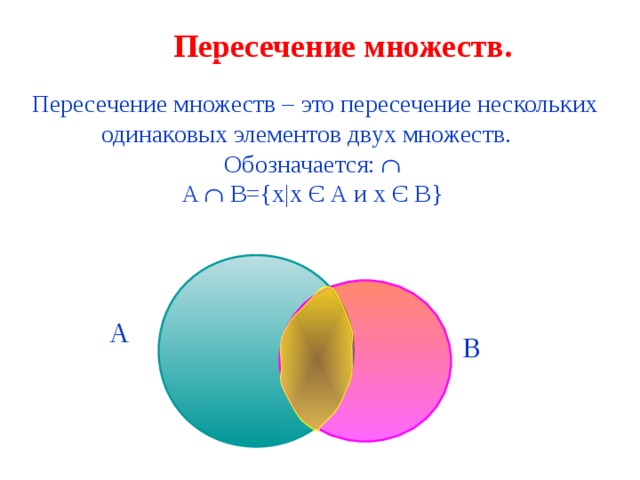
Пересечение множеств.
Пересечение множеств – это пересечение нескольких одинаковых элементов двух множеств.
Обозначается:
A B ={х| x Є A и x Є B }
А
В

Моя задача.
На полках стояло 20 дисков, причём на каждом есть запись. Известно, что 14 дисков с мультиками, а 16 с фильмами. На каком диске записаны и мультики, и фильмы?
Решение:
Пусть А – это множество дисков с записью мультиков. Количество элементов в нём, по условию: A = { 14 }
Пусть B – множество дисков с фильмами.
Количество элементов в нём: B={ 16 }
Пусть x – количество дисков с мультиками
и фильмами.
A + B -х=14+16-х=20 х= { 10 }
Ответ: на 10-ти дисках записаны
и мультики, и фильмы.
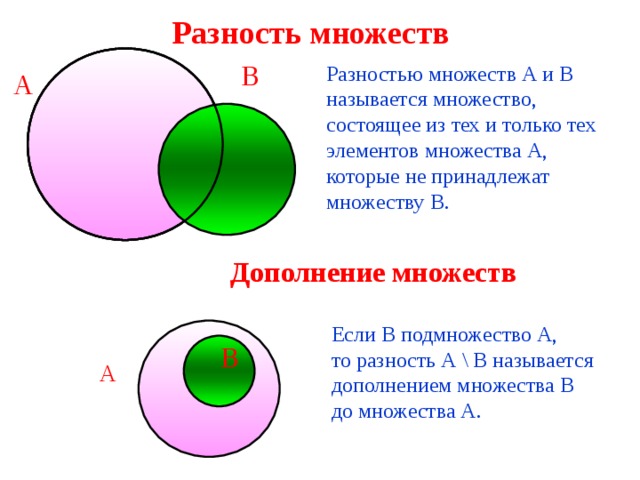
Разность множеств
В
Разностью множеств А и В
называется множество,
состоящее из тех и только тех
элементов множества А,
которые не принадлежат
множеству В.
А
Дополнение множеств
Если В подмножество А,
то разность А \ В называется
дополнением множества В
до множества А.
В
А

Моя задача.
На поляне летало четыре
вида бабочек. Синие с большим жёлтым кругом на крыльях. Красные с большим жёлтым кругом на крыльях. Красные и синие бабочки. Известно, что красных бабочек с жёлтым кругом было в два раза меньше, чем синих бабочек. Синих бабочек было 8, а синих с большим жёлтым кругом 5.
Всего бабочек было 21.
Сколько было красных бабочек?

Решение:
Сначала узнаем количество красных бабочек с жёлтыми кругами. Известно, что синих бабочек в 2 раза больше, количество элементов в множестве синих бабочек = { 8 }
1)8:2=4(б.)
Теперь мы можем узнать количество красных бабочек. Известно, что элементов в множестве синих бабочек с жёлтыми кругами = { 5 } , множество синих бабочек = { 8 } , ну а множество красных бабочек с кругами = { 4 } . Множество всех бабочек = { 21 }
2) 21-(5+8+4)=4(б.)
Ответ: множество красных бабочек равно { 4 } .

Мои исследования.
Сохраняют ли силу законы для чисел и для множеств? Я использовала специальные диаграммы, иллюстрирующие действия над множествами. Условилась обозначать множество всего класса квадратом, в этом квадрате можно расставить ряд точек, по числу учеников(Рис.1) .
Рис.1
18
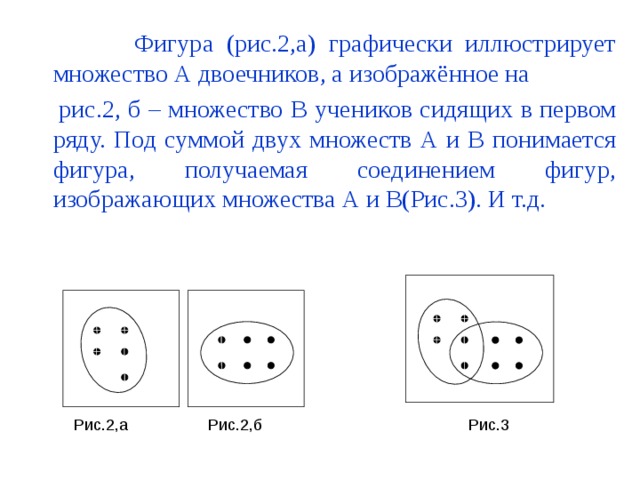
Фигура (рис.2,а) графически иллюстрирует множество A двоечников, а изображённое на
рис.2, б – множество B учеников сидящих в первом ряду. Под суммой двух множеств A и B понимается фигура, получаемая соединением фигур, изображающих множества A и B (Рис.3). И т.д.
Рис.2,а Рис.2,б Рис.3
19
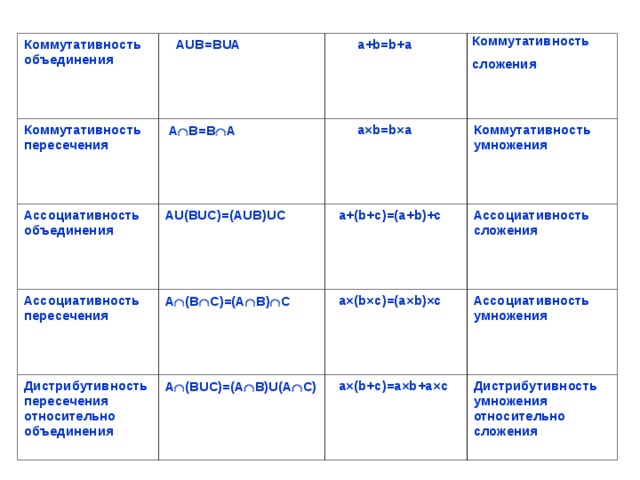
Коммутативность объединения
AUB=BUA
Коммутативность пересечения
а +b=b + a
A B=B A
Ассоциативность объединения
Коммутативность сложения
a×b=b×a
AU (В U С)=( AU В) U С
Ассоциативность пересечения
Дистрибутивность пересечения относительно объединения
Коммутативность умножения
а+( b + c ) = ( a + b ) +c
А (В С)=(А В) С
А (В U С)=(А В) U ( A C )
Ассоциативность сложения
a× ( b×c ) = ( a×b ) ×c
Ассоциативность умножения
a× ( b + c ) =a×b + a×c
Дистрибутивность умножения относительно сложения

Выводы:
- Я изучила основное понятие множества и операции над множествами, выявила значимость теории множеств в различных сферах жизни.
- Исследовала удивительную связь над операциями над множествами и обычными операциями с числами.
- Применила принципы теории множеств для расширения собственного мировоззрения в практической деятельности: при решении и составлении задач.
- В дальнейшем, я ставлю своей целью изучить раздел теории множеств: элементы математической логики, для расширения своего мировоззрения и применения в своей учебной деятельности, так как планирую в будущем поступить в институт экономики и финансов.

Выводы:
Теория множеств– это своего рода основа математического языка, без него невозможно заниматься математикой. Любая область человеческой деятельности связана не только с одним предметом, объектом, а с целой совокупностью объектов.






