ПРОЕКТ «Графы»
Автор работы: Ганина Анастасия
Преподаватель: Михайлова М.М.
Учреждение: МОУ СОШ №101
Класс: 8 «а»
Математика в практической
деятельности
Тема: «Графы и их применение»
2022-2023 уч. год.
Введение
Если вы любите решать задачи на смекалку или головоломки, то,
наверное, составляли таблицы, изображали объекты точками, соединяли
их отрезками или стрелками, выполняли над точками и отрезками
операции, не похожие на арифметические, алгебраические или
геометрические преобразования, то есть вам приходилось строить
математический аппарат специально для решения задачи. А это означает,
что вы заново открывали для себя начала теории графов.
Впервые с задачами, для решения которых используются графы, я
встретилась на олимпиаде по математике. Трудности в решении этих задач
объяснялись отсутствием этой темы в обязательном курсе школьной
программы. Возникшая проблема стала главной причиной выбора темы
данной исследовательской работы.
Цели и задачи:
Познакомиться с понятием “граф”, с его основными элементами:
вершина, ребра.
Научиться составлять и читать графы по словесному описанию
отношений между предметами и существами.
Развить логическое и образное мышление, воображение.
Показать связь с другими областями знаний.
Исследовать роль графов в нашей жизни.
Научиться решать задачи при помощи графов.
Актуальность и новизна:
Теория графов находит применение в различных областях современной математики и ее многочисленных приложениях.
Решение многих математических задач упрощается, если удается использовать графы.
Представление данных в виде графа придает им наглядность и простоту.
История возникновения графов
Толчок к развитию теория графов получила на рубеже XIX и XX столетий, когда наибольший интерес стали вызывать работы по комбинаторике. Как отдельная математическая дисциплина теория графов была впервые представлена в работе венгерского математика Кёнига в 30-е годы XX столетия.
Основы теории графов как математической науки заложил в 1736 г.
Леонард Эйлер, рассматривая задачу о кенигсбергских мостах. Сегодня
эта задача стала классической.
Понятие «графа»
Граф — математическая абстракция реальной системы любой природы, объекты которой обладают парными связями. Граф как математический объект есть совокупность двух множеств — множества самих объектов, называемого множеством вершин, и множества их парных связей, называемого множеством рёбер. Элемент множества рёбер есть пара элементов множества вершин. При взгляде на географическую карту сразу бросается в глаза сеть железных дорог. Это типичный граф: кружочки обозначают станции - вершины графа, а соединяющие их пути - ребра. Инженер чертит схемы электрических цепей. Химик рисует
структурные формулы, чтобы показать, как в сложной молекуле с помощью валентных связей соединяются друг с другом атомы.
Историк прослеживает родословные связи по генеалогическому дереву. Военачальник наносит на карту сеть коммуникаций, по которым из тыла к передовым частям доставляется подкрепление. Социолог на сложнейшей диаграмме показывает, как подчиняются друг другу различные отделы одной огромной корпорации.
Что общего во всех этих примерах? В каждом из них фигурирует схема, состоящая из точек (они обозначают разветвления электрической цепи, атомы, людей, города и т.д.), соединённых между собой линиями.
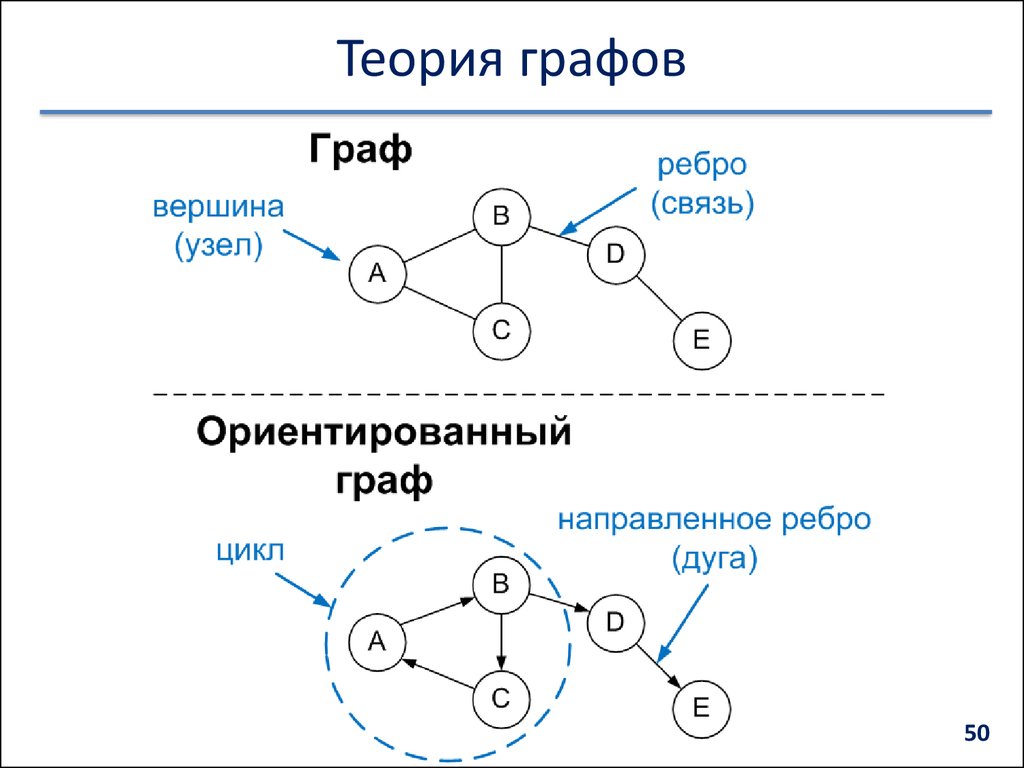
Виды графов
Ориентированный граф (кратко орграф) — рёбрам которого присвоено направление.
Неориентированный граф - это граф, в котором нет направления линий.
Взвешенный граф – дуги или ребра имеют вес.
Связный граф - в графе существует путь с концами А и В.
Несвязный граф - в графе не существует ни одного пути, связывающего их.
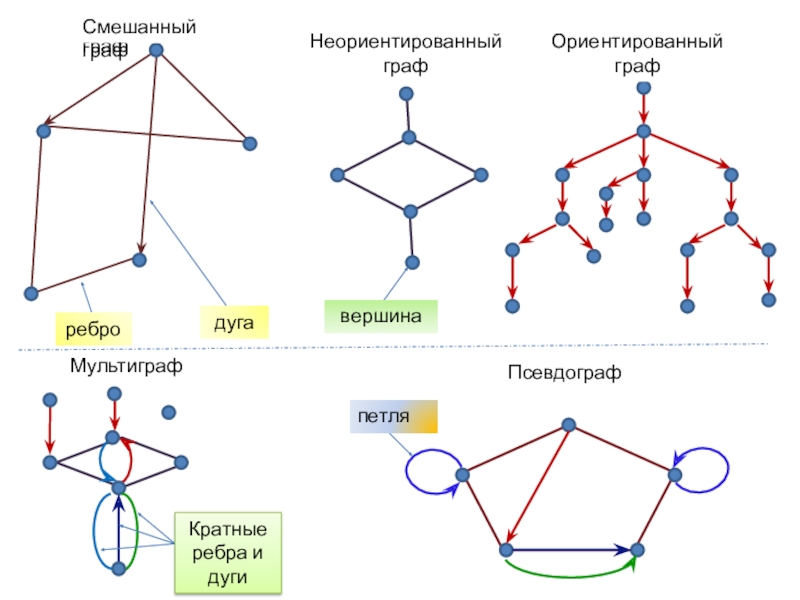
Полнота графа
Граф называется полным, если каждые две различные вершины его
соединены одним и только одним и только одним ребром
Эйлеров граф
Граф, который можно нарисовать, не отрывая карандаша от бумаги,
называется эйлеровым.
Решая задачу о кенигсбергских мостах, Эйлер сформулировал свойства графа:
Число нечётных вершин (вершин, к которым ведёт нечётное число рёбер) графа должно быть чётно. Не может существовать граф, который имел бы нечётное число нечётных вершин.
Если все вершины графа чётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой вершины графа и завершить его в той же вершине.
Граф с более чем двумя нечётными вершинами невозможно начертить одним росчерком.
Если все вершины графа четные, то можно не отрывая карандаш от бумаги («одним росчерком»), проводя по каждому ребру только один раз, начертить этот граф. Движение можно начать с любой вершины и закончить его в той же вершине.
Граф, имеющий всего две нечетные вершины, можно начертить, не отрывая карандаш от бумаги, при этом движение нужно начать с одной из этих нечетных вершин и закончить во второй из них.
Применение графов в реальной жизни
Графы нашли применение практически во всех отраслях научных знаний: физике, биологии, химии, математике, истории, лингвистике, социальных науках, технике и т.п. Наибольшей популярностью теоретико-графовые модели используются при исследовании коммуникационных сетей, систем информатики, химических и генетических структур, электрических цепей и других систем сетевой структуры.
Графы и информация
Двоичные деревья играют весьма важную роль в теории информации. Предположим, что определенное число сообщений требуется закодировать в виде конечных последовательностей различной длины, состоящих из нулей и единиц. Если вероятности кодовых слов заданы, то наилучшим считается код, в котором средняя длина слов минимальна по сравнению с прочими распределениями вероятности. Задачу о построении такого оптимального кода позволяет решить алгоритм Хаффмана.
Двоичные кодовые деревья допускают интерпретацию в рамках теории поиска. Каждой вершине при этом сопоставляется вопрос, ответить на который можно либо "да", либо "нет". Утвердительному и отрицательному ответу соответствуют два ребра, выходящие из вершины. "Опрос" завершается, когда удается установить то, что требовалось.
Таким образом, если кому-то понадобится взять интервью у различных людей, и ответ на очередной вопрос будет зависеть от заранее неизвестного ответа на предыдущий вопрос, то план такого интервью можно представить в виде двоичного дерева.
Графы и химия
Еще А. Кэли рассмотрел задачу о возможных структурах насыщенных (или предельных) углеводородов, молекулы которых задаются формулой: CnH2n+2.
Молекула каждого предельного углеводорода представляет собой дерево. Если удалить все атомы водорода, то оставшиеся атомы углеводорода также будут образовывать дерево, каждая вершина которого имеет степень не выше 4. Следовательно, число возможных структур предельных углеводородов, т. е. число гомологов данного вещества, равно числу деревьев с вершинами степени не больше четырех.
Таким образом, подсчет числа гомологов предельных углеводородов также приводит к задаче о перечислении деревьев определенного типа. Эту задачу и ее обобщения рассмотрел Д. Пойа.
Графы и биология
Деревья играют большую роль в биологической теории ветвящихся процессов. Для простоты мы рассмотрим только одну разновидность ветвящихся процессов – размножение бактерий. Предположим, что через определенный промежуток времени каждая бактерия либо делится на две новые, либо погибает. Тогда для потомства одной бактерии мы получим двоичное дерево.
Нас будет интересовать лишь один вопрос: в скольких случаях n-е поколение одной бактерии насчитывает ровно k потомков? Рекуррентное соотношение, обозначающее число необходимых случаев, известно в биологии под названием процесса Гальтона-Ватсона. Его можно рассматривать как частный случай многих общих формул.
Графы и физика
Еще недавно одной из наиболее сложных и утомительных задач для радиолюбителей было конструирование печатных схем.
Печатной схемой называют пластинку из какого-либо диэлектрика (изолирующего материала), на которой в виде металлических полосок вытравлены дорожки. Пересекаться дорожки могут только в определенных точках, куда устанавливаются необходимые элементы (диоды, триоды, резисторы и другие), их пересечение в других местах вызовет замыкание электрической цепи.
В ходе решения этой задачи необходимо вычертить плоский граф, с вершинами в указанных точках.
Теория графов находит применение в жизни. Например, помогут графы при нахождении наилучших вариантов развозки товаров по магазинам, материалов по стройкам. В терминах графов легко формулируется и решается задача о назначении на должности. Способ обходить все рёбра графа можно использовать для отыскания пути, позволяющего выбраться из лабиринта.
Простейшие задачи на графы
Задача 1
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Е?
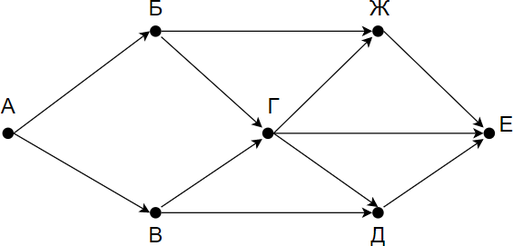
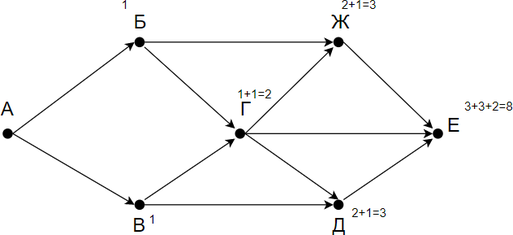
Решение:
Заметим, что количество путей в город Е является суммой путей в города Ж, Г и Д. Количество путей в город Ж — сумма путей в города Г и Б. Таким образом получаем: Г = Б + В Д = Г + В Ж = Б + Г Е = Ж + Г + Д.
Заметим, что в пункты Б и В можно попасть единственным способом — из города А. Отметим на рисунке индексами сверху каждого пункта количество путей, с помощью которых в него можно попасть и посчитаем итоговое.
Ответ: 8
Задача 2
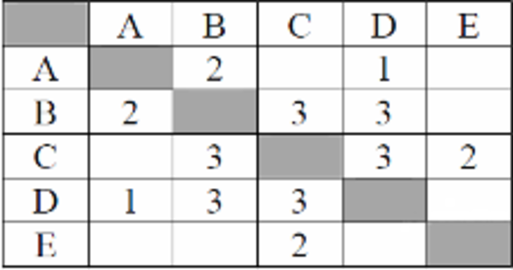
Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице: Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
Решение:
Найдём все варианты маршрутов из A в E и выберем самый короткий. Из пункта A можно попасть в пункты B, D. Из пункта B можно попасть в пункты C, D. Из пункта C можно попасть в пункты D, E. A—B—C—E: длина маршрута 7 км.
A—D—B—C—E: длина маршрута 9 км.
A—D—C—E: длина маршрута 6 км.
Самый короткий путь: A—D—C—E.
Длина маршрута 6 км.
Ответ: 6
Задача 3
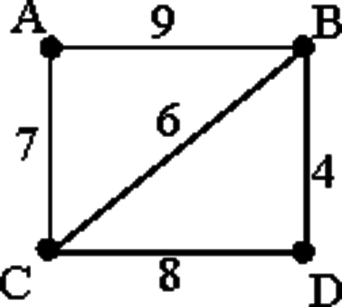
На схеме нарисованы дороги между четырьмя населёнными пунктами A, B, C, D и указаны протяжённости данных дорог. Определите, какие два пункта наиболее удалены друг от друга (при условии, что передвигаться можно только по указанным на схеме дорогам). В ответе укажите кратчайшее расстояние между этими пунктами.
Решение:
Заметим, что наиболее удалены друг от друга пункты A и D.
Найдём все варианты маршрутов из A в D и выберем самый короткий.
A—B—D: длина маршрута 13 км.
A—C—D: длина маршрута 15 км.
A—B—C—D: длина маршрута 23 км.
A—C—B—D: длина маршрута 17 км.
Заметим, что кратчайшее расстояние между пунктами A и D равняется 13.
Ответ: 13
Применение графов в жизни
В игре «майнкрафт» я строю дома и различную архитектуру. Что бы мне было легче понять площадь постройки и сам внутренний/внешний вид, я могу воспользоваться построением схемы через графы, как это делают архитекторы в реальной жизни.
Архитектура в майнкрафте Архитектура в реальной жизни

Заключение
Графы – замечательные математические объекты, с их помощью можно решать очень много различных, внешне не похожих друг на друга задач. Я исследовала только самые основные понятия, свойства графов и некоторые способы решения задач . Язык графов прост, доступен и понятен. Графовые задачи обладают рядом достоинств, позволяющих использовать их для развития соображения и улучшения логического мышления детей. Они допускают изложения в занимательной, игровой форме. С другой стороны, они труднее поддаются формализации, чем например, школьные задачи по алгебре, для их решения часто не требуется глубоких знаний, а следует применить смекалку. Выполняя данный проект я сделала вывод, что графы во многом облегчают нашу жизнь. Это относится не только о их применении в школе, но и в реальной жизни.
Я научилась использовать графы в своей любимой игре «майнкрафт».





