Числовая окружность

10 класс. Мордкович А.Г. Тригонометрические функции.

Числовая окружность

Валиева Ю.Ф.

Цель урока

• ввести понятие числовой окружности;
• формирование умения записывать множество чисел, соответствующих на числовой окружности точке;
• формирование умения находить на числовой окружности точку, соответствующую данному числу.

Числовая прямая

Прямая, на которой заданы точка отсчета, единичный отрезок и положительное направление, называется числовой прямой.

Определение?

Любому действительному числу можно сопоставить точку на числовой прямой , и наоборот.

Свойство?

Нанесите на числовую прямую числа π, 2 π, -π, - 2 π.

Нанесите на числовую прямую промежутки ( π ; 2 π ), [ - 2 π ; π / 2] .

-2π

-π

2π

π

0

6

-6

-3

1

-1

3

Числовая прямая

D

C

А

B

Запишите координаты точек :

Запишите промежутки и соответствующие неравенства:

1

проверка

[DA)

2

[BC]

проверка

A

C

B

D

π

-2π

2π

-π

t

0

0, то, двигаясь из точки А в направлении против часовой стрелки (положительное направление обхода окружности), опишем по окружности путь АМ длиной t, тогда М – искомая М(t).  Если t

Числовая окружность

+

R=1

А(0)

-

Определение.

Единичную окружность называют числовой окружностью , если между действительными числами и точками окружности установлено соответствие:

 Числу t = 0 сопоставлена точка А – правый конец горизонтального диаметра: А(0).

 Если t 0, то, двигаясь из точки А в направлении против часовой стрелки (положительное направление обхода окружности), опишем по окружности путь АМ длиной t, тогда М – искомая М(t).

 Если t

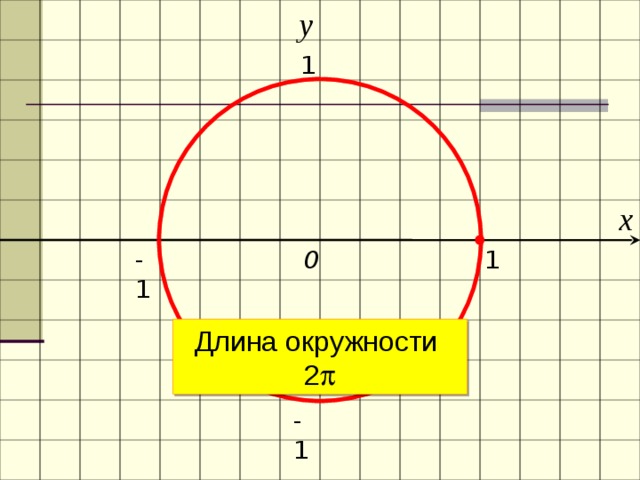
у

1

х

1

-1

0

Длина окружности 2 

-1

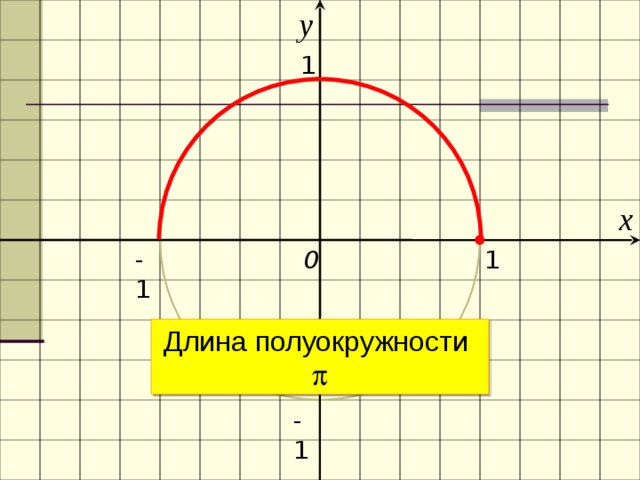
у

1

х

1

-1

0

Длина полуокружности 

-1

у



II

I



2 

2

3

3

5 



6

6

0



x

2 

7 

11 

6

6

4 

5 

III

IV

3 

3

3

2

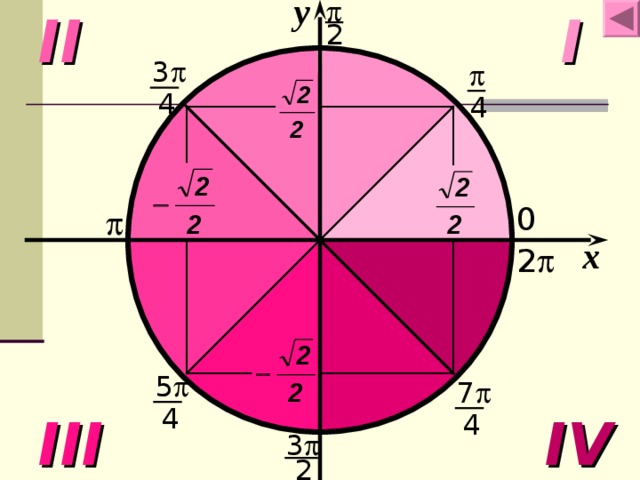
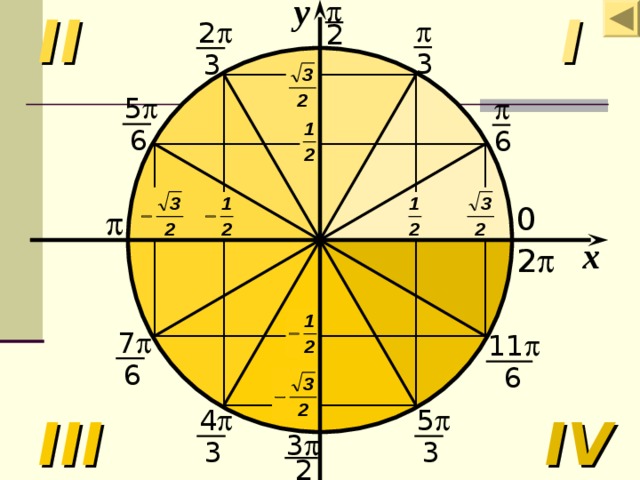
у



II

I

2

3 



4

4

0



x

2 

5 

7 

4

4

IV

III

3 

2

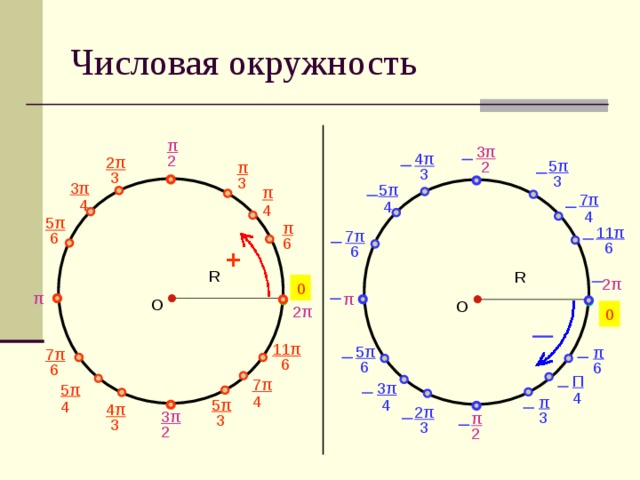
Числовая окружность

π

3π

4π

2

2π

5π

2

π

3

3

3

3

3π

5π

π

7π

4

4

4

4

5π

π

11π

7π

6

6

6

+

6

R

R

2π

0

π

π

О

О

2π

0

11π

5π

π

7π

6

6

6

6

Π

7π

3π

5π

4

4

π

5π

4

4

4π

2π

3π

3

π

3

3

3

2

2

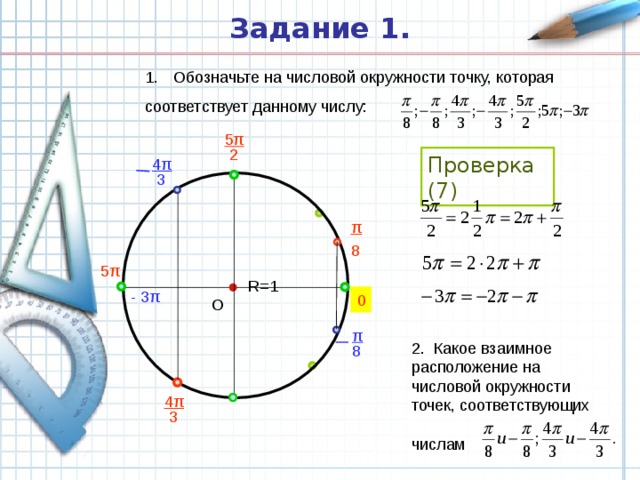
Задание 1.

• Обозначьте на числовой окружности точку, которая

соответствует данному числу:

5π

2

Проверка (7)

4π

3

π

8

5π

R=1

- 3 π

0

О

π

2. Какое взаимное расположение на числовой окружности точек, соответствующих числам

8

4π

3

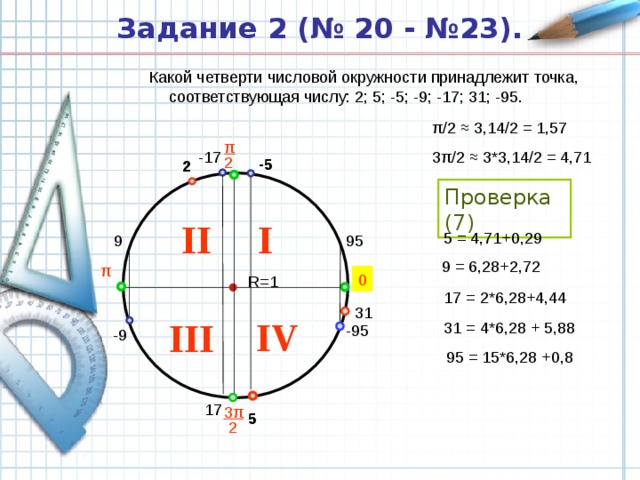
Задание 2 (№ 20 - №23).

Какой четверти числовой окружности принадлежит точка, соответствующая числу: 2; 5; -5; -9; -17; 31; -95.

π/2 ≈ 3,14/2 = 1,57

π

-17

3π/2 ≈ 3*3,14/2 = 4,71

2

-5

2

Проверка (7)

II

I

5 = 4,71+0,29

95

9

9 = 6,28+2,72

π

0

R=1

17 = 2*6,28+4,44

31

IV

III

31 = 4*6,28 + 5,88

-95

-9

95 = 15*6,28 +0,8

17

3π

5

2

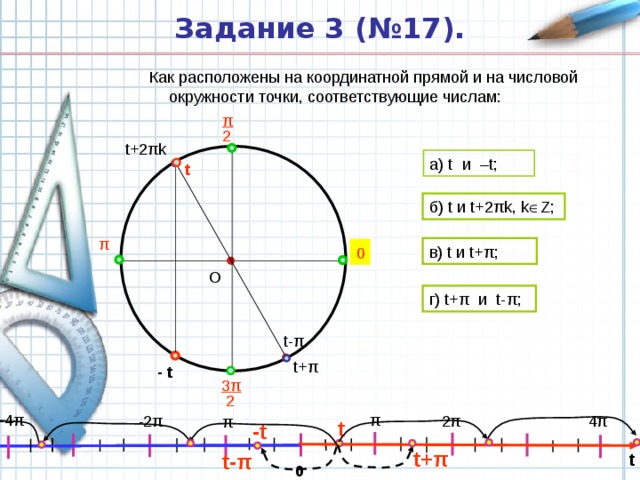
Задание 3 (№17).

Как расположены на координатной прямой и на числовой окружности точки, соответствующие числам:

π

2

t+2 πk

a) t и –t;

t

б) t и t+2 πk, k  Z;

π

в) t и t+ π ;

0

О

г) t+ π и t- π ;

t- π

t+ π

- t

3π

2

π

-4π

2π

4π

-2π

-π

t

-t

t+ π

t- π

t

0

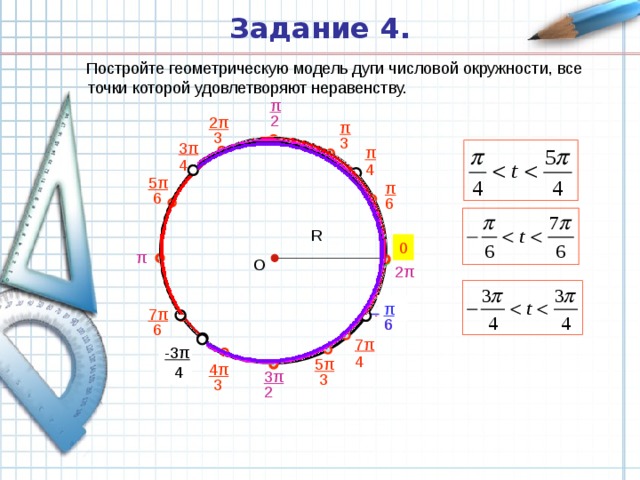
Задание 4.

Постройте геометрическую модель дуги числовой окружности, все точки которой удовлетворяют неравенству.

π

2

2π

π

3

3

3π

π

4

4

5π

π

6

6

R

0

π

О

2π

π

11π

7π

6

6

6

7π

5π

-3 π

4

4

5π

4

4π

3π

3

3

2

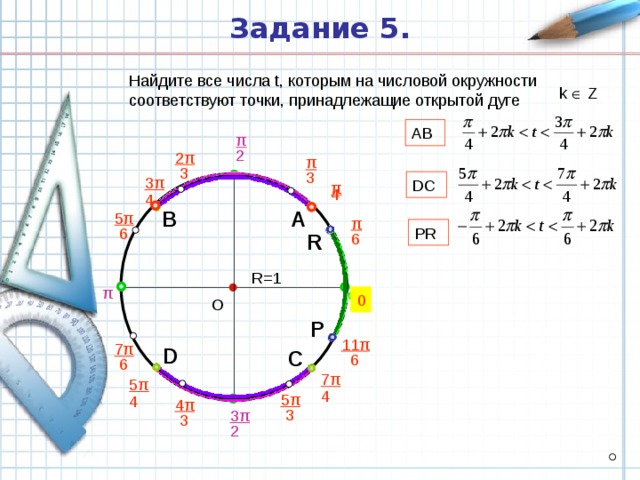
Задание 5.

Найдите все числа t, которым на числовой окружности соответствуют точки, принадлежащие открытой дуге

k  Z

AB

π

2

2π

π

3

3

3π

DC

π

4

4

А

В

5π

π

PR

6

6

R

R=1

π

0

О

P

11π

7π

D

С

6

6

7π

5π

4

5π

4

4π

3

3π

3

2

Итог урока

• Каким вопросам был посвящен урок?
• Чему научились на уроке?

Домашнее задание

§11 читать,

№ 11.2, 11.6-11.10(а,б),11.15- 11.16(б)

Источники

• А.Г. Мордкович, «Алгебра и начала анализа», 10 - 11 классы, часть 1, учебник.
• А.Г. Мордкович, «Алгебра и начала анализа», 10 - 11 классы, часть 2, задачник.