Анализ информации статистического характера

Тема 13. Элементы теории вероятностей. Элементы математической статистики.

Практическая работа № 51. Анализ информации статистического характера.

Проверяемые результаты обучения: У3, З1,З2, ОК1-ОК6.

Цель:систематизировать знания, умения и навыки по теме анализ информации статистического характера.

Время выполнения работы: 1 часа.

Задания.

Задача 1. В группе 30 студентов. Необходимо выбрать старосту, заместителя старосты и профорга. Сколько существует способов это сделать?

Задача 2. Два почтальона должны разнести 10 писем по 10 адресам. Сколькими способами они могут распределить работу?

Задача 3. В ящике 100 деталей, из них 30 – деталей 1-го сорта, 50 – 2-го, остальные – 3-го. Сколько существует способов извлечения из ящика одной детали 1-го или 2-го сорта?

Задача 4. Порядок выступления 7 участников конкурса определяется жребием. Сколько различных вариантов жеребьевки при этом возможно?

Задача 5. В конкурсе по 5 номинациям участвуют 10 кинофильмов. Сколько существует вариантов распределения призов, если по всем номинациям установлены различные премии?

Задача 6. В шахматном турнире участвуют 16 человек. Сколько партий должно быть сыграно в турнире, если между любыми двумя участниками должна быть сыграна одна партия?

Задача 7. В условиях задачи 6 определить, сколько существует вариантов распределения призов, если по всем номинациям установлены одинаковые призы?

Задача 8. Садовник должен в течении трех дней посадить 6 деревьев. Сколькими способами он может распределить по дням работу, если будет сажать не менее одного дерева в день?

Задача 9. Сколько существует четырехзначных чисел (возможно, начинающихся с нуля), сумма цифр которых равна 5?

Задача 10. Сколькими способами можно разбить группу из 25 студентов на три подгруппы А, В и С по 6, 9 и 10 человек соответственно?

Задача 11. В ящике 5 апельсинов и 4 яблока. Наудачу выбираются 3 фрукта. Какова вероятность, что все три фрукта – апельсины?

Задача 12. Преподаватель предлагает каждому из трех студентов задумать любое число от 1 до 10. Считая, что выбор каждым из студентов любого числа из заданных равновозможен, найти вероятность того, что у кого-то из них задуманные числа совпадут.

Задача 13. Найти вероятность того, что в 8-значном числе ровно 4 цифры совпадают, а остальные различны.

Задача 14. Шесть клиентов случайным образом обращаются в 5 фирм. Найти вероятность того, что хотя бы в одну фирму никто не обратится.

Задача 15. Пусть в урне имеется N шаров, из них М белых и N–M черных. Из урны извлекается n шаров. Найти вероятность того, что среди них окажется ровно m белых шаров.

Самостоятельная работа.

Задача 1. В ящике 10 красных и 5 синих пуговиц. Вынимаются наудачу две пуговицы. Какова вероятность, что пуговицы будут одноцветными?

Задача 2. Среди сотрудников фирмы 28% знают английский язык, 30% – немецкий, 42% – французский; английский и немецкий – 8%, английский и французский – 10%, немецкий и французский – 5%, все три языка – 3%. Найти вероятность того, что случайно выбранный сотрудник фирмы: а) знает английский или немецкий; б) знает английский, немецкий или французский; в) не знает ни один из перечисленных языков.

Задача 3. В семье – двое детей. Какова вероятность, что старший ребенок – мальчик, если известно, что в семье есть дети обоего пола?

Задача 4. Мастер, имея 10 деталей, из которых 3 – нестандартных, проверяет детали одну за другой, пока ему не попадется стандартная. Какова вероятность, что он проверит ровно две детали?

Задача 5. В одном ящике 3 белых и 5 черных шаров, в другом ящике – 6 белых и 4 черных шара. Найти вероятность того, что хотя бы из одного ящика будет вынут белый шар, если из каждого ящика вынуто по одному шару.

Задача 6. Три экзаменатора принимают экзамен по некоторому предмету у группы в 30 человек, причем первый опрашивает 6 студентов, второй — 3 студентов, а третий — 21 студента (выбор студентов производится случайным образом из списка). Отношение трех экзаменаторов к слабо подготовившимся различное: шансы таких студентов сдать экзамен у первого преподавателя равны 40%, у второго — только 10%, у третьего — 70%. Найти вероятность того, что слабо подготовившийся студент сдаст экзамен.

Задача 7. Фирма имеет три источника поставки комплектующих – фирмы А, B, С. На долю фирмы А приходится 50% общего объема поставок, В – 30% и С – 20%. Из практики известно, что среди поставляемых фирмой А деталей 10% бракованных, фирмой В – 5% и фирмой С – 6%. Какова вероятность, что взятая наугад деталь окажется годной?

Задача 8. Игральная кость брошена 6 раз. Найти вероятность того, что ровно 3 раза выпадет «шестерка».

Задача 9. Монета бросается 6 раз. Найти вероятность того, что герб выпадет не более, чем 2 раза.

Задача 10. Вероятность появления события в каждом из 400 независимых испытаний равна 0,8. Найти такое положительное число , чтобы с вероятностью 0,99 абсолютная величина отклонения относительной частоты появления события от его вероятности не превышала .

Задача 11.

Рост учащихся нашего класса

157,165,165,168,165,161,165,160,162,169,171, 170,170,175,173,170,177,182,186,182,160,173, 165,162,174,177.

1) составить ранжированный ряд ;

2) определить средний рост, моду ряда, медиану ряда.

Вопросы.

1.Какие задачи называются комбинаторными?

2.Событие, вероятность события, сложение и умножение вероятностей.

3.Понятие о независимости событий.

Критерии оценки практической работы:

4 балла: работа выполнена в полном объеме с соблюдением необходимой

последовательности действий:

- проводит работу в условиях, обеспечивающих получение правильных результатов и выводов;

- соблюдает правила техники безопасности;

- в ответе правильно и аккуратно выполняет все записи, таблицы, рисунки, чертежи, графики, вычисления;

- правильно выполняет анализ ошибок.

3 балла: работа выполнена правильно с учетом 1-2 мелких погрешностей или 2-3 недочетов, исправленных самостоятельно по требованию преподавателя.

1-2 балла: работа выполнена правильно не менее чем наполовину, допущены 1-2 погрешности или одна грубая ошибка.

0 баллов: выставляется, если выполнено не менее половины заданий, причем допущены грубые ошибки вычислительного характера и ошибки, показывающие незнание обучающимися формул, правил, основных свойств математики.

Тема 13. Элементы теории вероятностей. Элементы математической статистики.

Практическая работа № 52. Анализ реальных числовых данных, представленных в виде диаграмм, графиков.

Проверяемые результаты обучения: У3, З1,З2, ОК1-ОК6.

Цель: систематизировать знания, умения и навыки по теме анализ реальных числовых данных, представленных в виде диаграмм, графиков.

Время выполнения работы: 2 часа.

Задания.

1. На шоссе длиной 100 км имеется 10 гаражей. Для проектирования строительства бензоколонки были собраны данные о числе предполагаемых поездок на заправку с каждого гаража. Результаты обследования приведены в таблице.

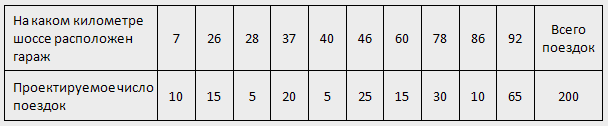
Бензоколонку нужно поставить так, чтобы общий пробег машин на заправку был наименьшим.

1. Поезда метрополитена идут регулярно с интервалом 2 мин. Пассажир выходит на перрон в случайный момент времени, никак не связанный с расписанием. Случайная величина – время Т, в течение которого ему придется ждать поезда. Найти плотность распределения, математическое ожидание, дисперсию, среднее квадратичное отклонение и вероятность того, что ждать пассажиру придется не больше полминуты.

2. Случайная величина Х имеет показательное распределение с параметром 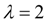. Найти вероятность события {1

3. Магазин получает электролампочки с двух заводов, причем доля первого завода составляет 25 %. Известно, что доля брака на этих заводах равна соответственно 5 % и 10 % от всей выпускаемой продукции. Продавец наугад берет одну лампочку. Какова вероятность того, что она окажется бракованной?

Самостоятельная работа

Вариант 1.

1. Бросается 5 монет. Какова вероятность того, что три раза выпадет герб?

2. Быстро вращающийся диск разделен на четное число равных секторов, попеременно окрашенных в белый и черный цвет. По диску произведен выстрел. Найти вероятность того, что пуля попадет в один из белых секторов. Предполагается, что вероятность попадания пули в плоскую фигуру пропорциональна площади этой фигуры.

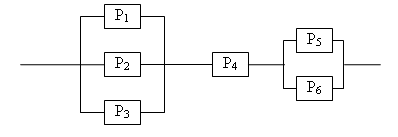
3. Определить надежность схемы, если P_i – надежность i – го элемента

1. Дан ряд распределения дискретной случайной величины. Определить значение x.

   1	2	3	4
   0,1	х	0,2	0,4

2. Найти доверительный интервал для оценки математического ожидания m нормального закона с надежностью 0.9; зная выборочную среднюю .

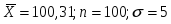3. Задана матрица вероятностей перехода для цепи Маркова за один шаг. Найти матрицу перехода данной цепи за два шага.

4. DX = 1.5. Используя свойства дисперсии, найдите D(2X+5).

5. Рассматривается круглосуточная работа пункта проведения профилактического осмотра автомашин с одним каналом (одной группой проведения осмотра). На осмотр и выявление дефектов каждой машины затрачивается в среднем 0,4 часа. На осмотр поступает в среднем 36 машин в сутки. Если машина, прибывшая в пункт осмотра, не застает ни одного канала свободным, она покидает пункт осмотра необслуженной. Определить вероятности состояний и характеристики обслуживания профилактического пункта осмотра.

Вариант 2.

1. Бросается 6 монет. Какова вероятность того, что герб выпадет более четырех раз?

2. В круг радиусом 10 помещен меньший круг радиусом 5. Найти вероятность того, что точка, наудачу брошенная в большой круг, попадет также и в малый круг. Предполагается, что вероятность попадания точки в круг пропорциональ­на площади круга и не зависит от его расположения.

3. Определить надежность схемы, если P_i – надежность i – го элемента

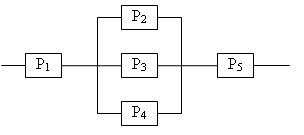
1. Дан ряд распределения дискретной случайной величины. Определить математическое ожидание случайной величины.

   1	2	5	6
   0,2	0,1	0,6	х

2. Найти доверительный интервал для оценки математического ожидания m нормального закона с надежностью 0.95; зная выборочную среднюю .

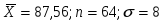3. Задана матрица вероятностей перехода для цепи Маркова за один шаг. Найти матрицу перехода данной цепи за два шага.

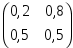4. MX = 1.5. Используя свойства математического ожидания, найдите M(2X+5).

5. Рассматривается круглосуточная работа пункта проведения профилактического осмотра автомашин с четырьмя каналами (четырьмя группами проведения осмотра). На осмотр и выявление дефектов каждой машины затрачивается в среднем 0,5 часа. На осмотр поступает в среднем 20 машин в сутки. Если машина, прибывшая в пункт осмотра, не застает ни одного канала свободным, она покидает пункт осмотра необслуженной. Определить вероятности состояний и характеристики обслуживания профилактического пункта осмотра. Найти число каналов, при котором относительная пропускная способность пункта осмотра будет не менее 0,9.

Вопросы.

1. Способы выборки.

2. Средняя арифметическая, средняя гармоническая, средняя квадратичная, геометрическая.

Критерии оценки практической работы:

4 балла: работа выполнена в полном объеме с соблюдением необходимой

последовательности действий:

- проводит работу в условиях, обеспечивающих получение правильных результатов и выводов;

- соблюдает правила техники безопасности;

- в ответе правильно и аккуратно выполняет все записи, таблицы, рисунки, чертежи, графики, вычисления;

- правильно выполняет анализ ошибок.

3 балла: работа выполнена правильно с учетом 1-2 мелких погрешностей или 2-3 недочетов, исправленных самостоятельно по требованию преподавателя.

1-2 балла: работа выполнена правильно не менее чем наполовину, допущены 1-2 погрешности или одна грубая ошибка.

0 баллов: выставляется, если выполнено не менее половины заданий, причем допущены грубые ошибки вычислительного характера и ошибки, показывающие незнание обучающимися формул, правил, основных свойств математики.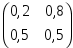