Технологическая карта урока на тему:
«Исследование функций».
Учитель математики Алишейхова П.А.
Продолжительность урока: 1 урока 45 минут.
Цель урока:
1.Систематизировать знания по теме «Свойства функций»
2.Уметь проводить исследование функций
3.Уметь «читать» графики функций
Задачи урока:
Образовательные − обобщить и систематизировать знания обучающихся по данной теме; формировать у обучающихся умения исследовать функции; отработать навыки построения графиков функций;
Развивающие − развитие умений применять теоретические знания при исследовании функций; развитие исследовательских умений, навыков самостоятельной работы, развитие умения рассуждать, сравнивать, обобщать, формулировать выводы, развитие мышления, памяти, внимания и математического кругозора;
Воспитательные − воспитание воли и упорства для достижения конечного результата; воспитание познавательной активности, аккуратности при построении графиков, прививать интерес к предмету математики, воспитывать сознательное отношение к обучению, самостоятельности.
Формы организации урока: фронтальная, индивидуальная, групповая.
Оборудование: компьютер, мультимедийный проектор, экран, тесты, схемы исследования функций.
(Урок объяснение новой темы)
ОБЩАЯ ЧАСТЬ
Предмет - алгебра
Класс - 10
Тема урока – «Исследование функций».
Планируемые образовательные результаты
Предметные
Метапредметные
Личностные
Систематизировать знания по теме «Свойства функций»
Уметь проводить исследование функций
Уметь «читать» графики функций
Коммуникативные: вступать в учебный диалог с учителем; участвовать в общей беседе, строить монологические высказывания
Регулятивные: планировать необходимые действия, операции; оценивать возникающие трудности; вносить коррективы в работу; контролировать процесс и результаты деятельности; формирование компетентности в области ИКТ; адекватно оценивать свои возможности достижения цели
Познавательные: читать и слушать, извлекая необходимую информацию; осознавать познавательную задачу
Формирование положительного отношения к учебе, желание приобретать новые знания; совершенствовать имеющиеся знания, умения.
Ресурсы урока: интерактивная доска, компьютер, мультимедийный проектор, ноутбук, раздаточный материал
ОРГАНИЗАЦИОННАЯ СТРУКТУРА УРОКА
Этап урока (+время)
Деятельность учителя
Деятельность учащихся
1 этап. Организационный момент (1 мин)
Приветствие, создание благоприятного психологического настроя, мобилизация внимания учащихся.
Самоопределение, оценка готовности к уроку, включение в деловой ритм урока.
2этап. Актуализация знаний (5мин)
Проверка домашнего задания с целью выделения тех знаний, которые наиболее важны на данном уроке (приложение)
Задают вопросы, оценивают правильность ответа на поставленный вопрос; оценивают домашнюю работу по кроссворду
3 этап. Мотивация (3 мин)
1. Создание проблемной ситуации при помощи исторического материала, с последующим определением темы урока (приложение)
2. Знакомство с листом самооценки (приложение)
Выделение существенной информации из слов учителя при построении темы урока; проявляют навыки логично выражать свои мысли, вступая в диалог с учителем и одноклассниками.
4 этап. Целеполагание и планирование
(3 мин)
Сообщает целевые установки урока, намечает план предстоящей работы (приложение)
Делают записи в тетради; осмысливают поставленные задачи и цели.
5 этап. Применение знаний и умений в новой ситуации (9мин)
Повторить все свойства функции. И все эти свойства можно объединить в одну схему, по которой можно исследовать любые функции. Ребята, как вы думаете, какая тема сегодняшнего урока. (исследование функций). Чему мы должны научиться? (Исследовать функции, используя их свойства). Вот схема, которая нам поможет выполнять построение и чтение графиков. (поговорить о схеме)
Мы с вами вместе разберем один график какой-нибудь функции по этой схеме.
Совместная работа с учителем
6 этап. Обобщение и систематизация знаний (5 мин)
Задает устные вопросы по графикам, изображенным на интерактивной доске, реализуя здоровьесберегающие технологии, проводит физминутку (приложение)
Дают устные ответы и принимают участие в физминутке
7 этап. Развитие исследовательских навыков при чтении графика функции (10 мин)
Краткая история о названии функции.
Работа по учебному материалу. Задание из банка ФИПИ по ЕГЭ
Ученики ведут исследование в тетради, по одному ученику у доски записывают одно из свойств функции, предварительно выполняя необходимые записи или решение математической модели, вспоминают определения. Строят график в тетради, сверяя его с графиком, построенным на доске
8 этап. Контроль знаний и умений по теме (5мин)
Самостоятельная работа в тетрадях в виде тестов
Работают над тестами и взаимопроверяют
9 этап. Информация о домашнем задании
(1 мин)
Домашнее задание (дифференцированный подход) (приложение 8)
Записывают домашнее задание в дневник.
10 этап. Рефлексия (3 мин)
Дает качественную оценку работы класса
и отдельных учеников, инициирует рефлексию учеников по поводу мотивации их деятельности и взаимодействия с учителем и учениками класса. Предлагает заполнить дорожную карту
Заполняют дорожную карту, и выставляют самооценку за урок, некоторые делятся своими записями с учителем и одноклассниками.
Приложение
Здравствуйте ребята и уважаемые гости.
Я бы хотела начать урок с афоризма Дьёрдя Пойа «Лучший способ изучить что-либо – это открыть самому»
Ребята возникли ли у вас вопросы при выполнении домашнего задания. (нет)
Тогда давайте мы с вами сейчас решим кроссворд, в котором мы повторим необходимый материал для новой темы.
Если функция непрерывна в каждой точке данного промежутка ее называют…(непрерывная)
Если для любого х из ее области определения f(-x) = f(x), то функцию называют … (четная) Скажите пожалуйста ребята, график четной функции симметричен относительно чего? (относительно оси ординат)
Если для любого х из ее области определения f(-x) = - f(x), то функцию называют … (нечетная) А график нечетной функции симметричен относительно чего? (относительно начала координат)
Функция, повторяющая свои значения через какой-то не нулевой период, то есть не меняющая своего значения при добавлении к аргументу фиксированного не нулевого числа, называется… (периодическая)
Большему значению аргумента соответствует большее значение функции т.е. если для любых х1 и х2 из множества Р, таких что х2x1, выполнено неравенство f(x2) f(x1), то функцию называют …. (возрастающая)
Большему значению аргумента соответствует меньшее значение функции т.е. Если для любых х1 и х2 из множества Р, таких что х2x1, выполнено неравенство f(x2)
Значение независимой переменной при которых функция принимает значение, равное 0, называется… (нулями функции)
Промежутки, в которых функция принимает значение одного итого же знака, называют промежутками… (знакопостоянства)
Точки максимума и минимума объединяют общим термином … (экстремум)
Мы с вами сегодня говорим о функциях. Как вы думаете, где они используются? (для сдачи ЕГЭ). Я вам приведу несколько примеров, где функция применяется в повседневной жизни. Например, экономист использует такие функции как: функции спроса, функции издержек, функция полезности. Показательная функция применяется в физике – это радиоактивный распад, изменение атмосферного давления с изменением высоты охлаждения тел. В химии - цепные реакции, в биологии – рост колоний живых организмов. Есть такая функция как, выбрасывание инсулина в кровь. К сожалению, у нас с вами не так много времени, поэтому подробно рассмотреть эти функции мы с вами не сможем.
Но вы уже наверно убедились в том, какую важную роль играет функция в нашей жизни. Все свойства, которые мы с вами повторили, можно объединить в одну схему, по которой можно исследовать функции. Ребята, как вы думаете, какая же тема сегодняшнего нашего урока. (исследование функций). Чему мы должны научиться? (Исследовать функции, используя их свойства). Вот схема, которая нам поможет выполнять построение и чтение графиков. (поговорить о схеме)
Найти область определения функции.
Найти область значений функции.
Определить чётность или нечётность функции, периодичность.
Найти координаты точек пересечения графика с осями координат. Нули функции.
Найти промежутки знакопостоянства функции.
Определить промежутки возрастания или убывания функции.
Найти точки экстремума функции (максимум или минимум) и значения функции в этих точках.
Построить график функции.
И так первым пунктом у нас идет Область определения функции. Как вы будете находить ее? (Это такие значения независимой переменной при которых функция имеет смысл) Вторым пунктом идет область значения функции. Ее как найдете? (Это значения зависимой переменной в котором определена функция) Ребята, а знаете ли вы какую-нибудь периодическую функцию? Кто может привести пример? (синусоида, косинусоида). Остальные все свойства мы уже повторили.
Сейчас мы с вами вместе разберем один график какой-нибудь функции по этой схеме. (разбор функции)
D(f) (-8;3)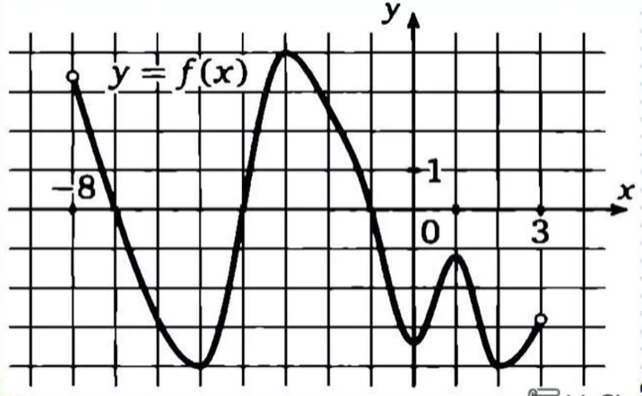
E(f) [-4;4]
Ни четная и ни нечетная, не периодическая
Нули функции -7;-4;-1.
Промежутки знакопостоянства положительные (-8;-7),(-4;-1) отрицательные (-7;-4),(-1;3)
Убывает функция (-8;-5), (-3;0), (1;2) Возрастает (-5;-3), (0;1), (2;3)
Экстремумы функции max -3, 1 min -5, 0, 2
Ребята скажите, а вы любите проводить время за компьютером? (да) И сколько же времени вы уделяете в день? (ответы детей) А вы знаете какое количество времени полагается проводить вам за компьютером в вашем возрасте? А ведь это тоже функция «Время за компьютером в зависимости от возраста». Как вы думаете от каких переменных зависит эта функция? (зависимость времени от возраста). Наша функция возрастающая или убывающая? (возрастающая) Как вы думаете к чему может привести длительное времяпровождение за компьютером? (к ухудшению зрения) Что бы наше зрение немного улучшить мы сейчас выполним профилактическое упражнение для глаз. (под музыку выполняют упражнения). Выполнить первые 8 пунктов.
Рекомендую проводить вам такое упражнение каждый день, а чтобы вы не забыли как его выполнять я поделюсь с вами материалом. Ну что немного отдохнули?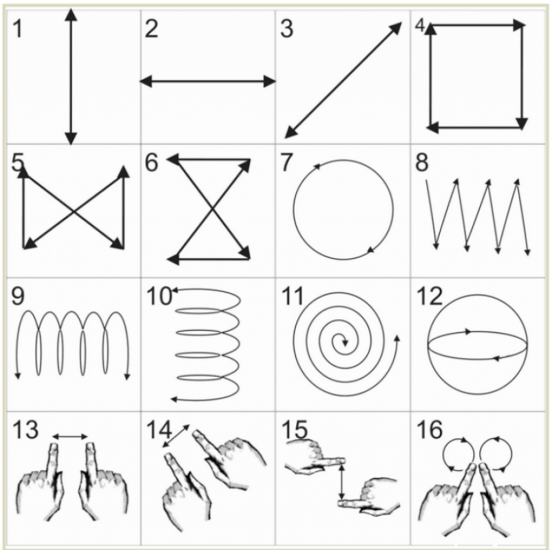
А сейчас мы с вами откроем учебники на странице 55 и выполним номер 93 (а,г), использую данную схему, которая у всех есть на партах, но выполним его разделившись на минигруппы. (по парам). На это задание я вам даю три минутки. Ответы запишите в тетрадях. (Ответы на доске для проверки)
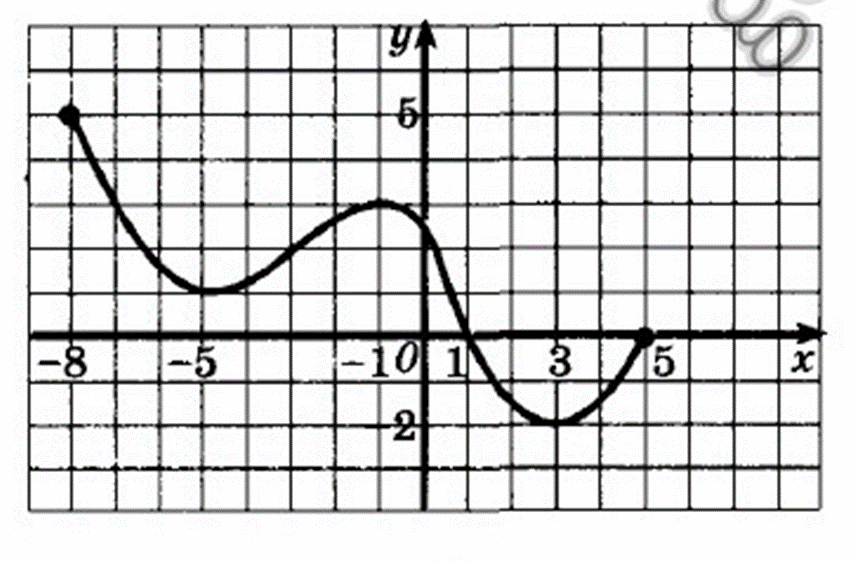
1. D(f) [-8;5]
2. E(f) [-2;5]
3. Ни четная и ни нечетная, не периодическая
4. Нули функции 1;5.
5. Промежутки знакопостоянства положительные (-8;1),
отрицательные (1;5)
6. Убывает функция (-8;-5), (-1;3), Возрастает (-5;-1), (3;5)
7. Экстремумы функции max -1, min -5, 3
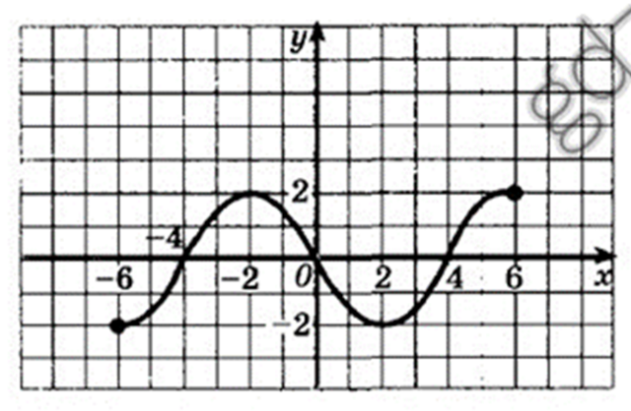
1. D(f) [-6;6]
2. E(f) [-2;2]
3. Ни четная и ни нечетная, не периодическая
4. Нули функции -4;0;4.
5. Промежутки знакопостоянства положительные (-4;0), (4;6) отрицательные (-6;-4),(0;4)
6. Убывает функция (-2;2), Возрастает (-6;-2), (2;6)
7. Экстремумы функции max -2, min 2
Ребята то, что, мы сейчас с вами выполняли называют «чтением» графиков. Нам задан график функции, с помощи которого мы перечисляли основные свойства этой функции. Такие задания у вас будут на ЕГЭ. Давайте попытаемся решить одно задание из банка ФИПИ

(задать дополнительный вопрос: Сколько дней было меньше чем 0,3 миллиметров осадков. Ответ 6.)
А сейчас мы с вами выполним самостоятельную работу на 5 минут (по теме исследование функции).
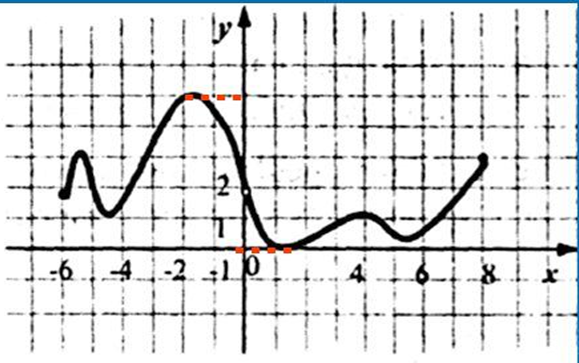
1.D(f) [-6;8]
2.E(f) [0;5]
3.Ни четная и ни нечетная, не периодическая
4.Нули функции 1
5.Промежутки знакопостоянства положительные [-6;1), (1;8]
отрицательные (нет)
6.Убывает функция (-5;-4), (-2;1), (4;5,5)
Возрастает (-6;-5), (-4;-2), (1;4), (6;8)
7.Экстремумы функции
max -5, -2,4, min -5; 1; 5,5
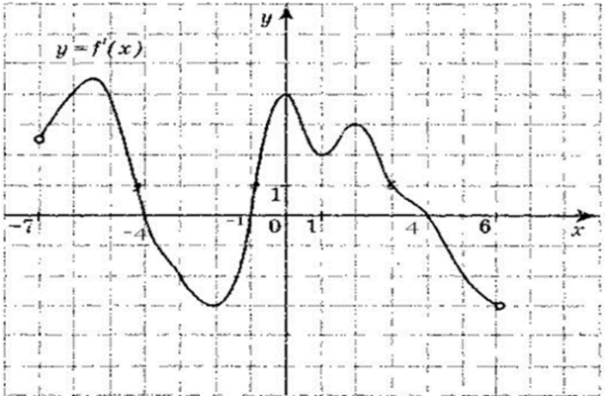
1.D(f) (-7;6)
2.E(f) [-3;4,5]
3.Ни четная и ни нечетная, не периодическая
4.Нули функции -4;-1;4.
5.Промежутки знакопостоянства положительные (-7;-4), (-1;4) отрицательные (-4;-1),(4;6)
6.Убывает функция (-5,5;-2), (0;1), (2;6)
Возрастает (-7;-5,5), (-2;0), (1;2)
7.Экстремумы функции
max 5,5; 0; 2, min -2;1
(взаимопроверка). А теперь мы обменяемся тетрадями и проверим работу соседа. Оценку поставьте карандашом. Нет ошибок «5», 1-2 ошибки «4», 3-4 ошибки «3». (Ребята поднимите руки те, кто получил «5», а теперь те, кто «4», есть ли у нас ученики, которые получили «2»?)
Сегодня мы с вами учились читать графики по схеме, а на следующем уроке вы будете учиться строить графики по заданным свойствам.
А теперь давайте разберем домашнюю работу, которая у вас у всех лежит на партах. Там всего 3 номера, вам нужно выбрать из них те, которые вы сможете решить. Если вы выбираете все три задания значит вы решаете на «5», если 2 задания «4», ну а если одно задание, то – «3». Кто выбрал все задания? А кто 1 задание? Хорошо, молодцы ребята.
Ну а теперь давайте мы с вами подведем итоги урока.
У каждого из вас на парте есть дорожная карта, где вам необходимо сделать самооценку свой работы на этом уроке. В третьем столбике вы выставляете себе баллы, а во втором столбике указаны критерии баллов, т.е. сколько вам необходимо ставить баллов за выполненную работу на уроке. Ну что ребята вы поставили себе баллы? Ну а теперь давайте поставим и оценку. Если вы набрали 12-11 баллов - «5», 10-9 балла – «4», 8-6 баллов – «3».
Ребята перед вами есть незаконченные смайлики. Я бы хотела, чтобы вы дорисовали смайлик, показав этим свое настроение и понравился ли вам урок. Обратите внимание на варианты смайликов. Те, у кого совпадает с моим настроением, магнитиком прикрепите на мой смайлик, а те, у кого не совпадает с моим смайликом рядом. Спасибо за внимание.





