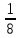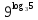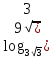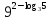Урок математики в 11 классе "Числа и вычисления"

Тема урока: «Числа и вычисления»

Обучающая цель урока: предполагается, что в ход урока

учащиеся:

• Обобщат понятие числовых множеств

• Повторят понятие логарифма числа по данному основанию

• Усовершенствуют свои умения по выполнению заданий с логарифмами

Задачи личностного развития:

• Способствовать развитию умения анализировать, делать выводы.

• Создать условия для развития самостоятельности учащихся

• Создать условия для развития творческих способностей учащихся

Тип урока: урок повторения

Учебно-методическое обеспечение:

учебное пособие 11 класс §19, рабочая тетрадь, проектор, презентация, компьютеры, электронный тест для проведения промежуточного контроля, карточки для ответов на вопросы теста

Ход урока

1. Организационный момент

Мы с вами приступили к повторению курса математики, изученного в школе. И начали мы с темы «Числа и вычисления». Назовите по одной ассоциации со словом «число».

1. Целемотивационный этап

Давайте еще раз вспомним, с какими числами мы познакомились на уроках математики

Сообщение «Множества чисел» (Приложение 1, Презентация слайды 2-5)

Как было только что сказано, логарифмы, за редким исключением, являются иррациональными числами. И на сегодняшнем уроке мы повторим с вами понятие логарифма и основные свойства логарифмирования.

1. Актуализация знаний и умений учащихся

   1. Фронтальная работа: (Учащиеся отвечают на вопросы, которые заранее были предложены в качестве домашнего задания для повторения. Формулы отображаются в презентации - слайд 7, приложение 3)

      1. Какое число называется логарифмом данного числа по данному основанию?

      2. Каким может быть основание логарифма?

      3. Каким может быть подлогарифмическое выражение?

      4. В чем заключается основное логарифмическое тождество?

      5. Чему равен логарифм 1?

      6. Чему равен логарифм основания?

      7. Чему равен логарифм произведения?

      8. Чему равен логарифм частного?

      9. Чему равен логарифм степени?

      10. Какой логарифм называется десятичным?

      11. Какой логарифм называется натуральным?

      12. Как перейти к логарифму с новым основанием?

1. Устный счет № 981 (1 и 3 столбики) № 982 (б, е)

(№№ на слайде)

1. Выполнение практических заданий (№№ на слайде)

№ 984 а

№ 985 а (б* дополнительно)

1. Тестовое задание (Приложение 2, 4)

Выполнение тестов, созданных в Гугл-форме. Результат выполнения каждого учащегося отображается в сводной электронной таблице.

Учащиеся заполняют формы приложения 4.

Анализ выполненных тестов

1. Информация о домашнем задании

№ 984 (б, г), 984 (в-e)

1. Подведение итогов

Как вы оцениваете свою работу?

Определение темы следующего урока. (Приложение 5)

Составить из букв соответствующих правильным вариантам ответов на тестовые задания слово (ВЫРАЖЕНИЕ). Тема следующего урока «Выражения и их преобразование»

1. Рефлексия

Продолжите фразы:

• У меня получилось…

• Самым трудным было…

Приложение 1

Натуральные числа — это числа, которые используют при счете предметов.

Наименьшее натуральное число — единица. Нуль не является натуральным числом.

Все натуральные числа образуют множество натуральных чисел(N).

Наибольшего натурального числа не существует. Множество натуральных чисел бесконечно.

Во множестве натуральных чисел всегда выполнимы действия сложения и умножения, а действие вычитания выполнимо не всегда.

Для натуральных чисел можно сформулировать признаки делимости:

Признак делимости на 2	Число делится на 2, если оно оканчивается четной цифрой
Признак делимости на 3	Число делится на 3, если сумма его цифр делится на 3
Признак делимости на 4	Натуральное число делится без остатка на 4, если сумма предпоследней цифры в его записи и половины последней цифры — четное число
Признак делимости на 5	Число делится на 5, если оно оканчивается цифрой 0 или цифрой 5
Признак делимости на 9	Число делится на 9, если сумма его цифр делится на 9
Признак делимости на 10	Число делится на 10, если оно оканчивается на 0
Признак делимости на 11	Число делится на 11, если сумма цифр, которые стоят на четных местах, равна сумме цифр, стоящих на нечетных местах, либо отличается от неё на число, которое делится на 11.

Натуральное число, имеющее точно два различных натуральных делителя, называется простым числом, а число, имеющее более двух различных натуральных делителей, называется составным числом. Число 1 не является простым и не является составным.

Любое натуральное число можно представить в виде произведения простых множителей. На этом основываются алгоритмы нахождения наибольшего общего делителя (НОД) и наименьшего общего кратного (НОК) чисел.

Если к натуральным числам присоединить противоположные им числа −1, −2, −3, … и число 0, то образуется множество целых чисел.

Во множестве целых чисел всегда выполнимы действия сложения, вычитания и умножения, а действие деления, во множестве целых чисел остается не всегда выполнимым.

Множество, состоящее из всех целых и дробных чисел, называется множеством рациональных чисел (Q). Во множестве рациональных чисел всегда выполнимы действия сложения, вычитания, умножения и деления (кроме деления на 0).

Каждое рациональное число можно единственным образом представить обыкновенной несократимой дробью , где m целое число, n натуральное. Рациональные числа можно представлять и десятичными дробями, конечными или бесконечными периодическими.

Некоторые часто используемые дроби имеют специальные названия. Сотая доля называется процентом, а тысячная — промилле.

Число, не являющееся рациональным, называется иррациональным. Иррациональными числами являются числа  и е. Результаты действий извлечения корня, нахождения значений тригонометрических функций, логарифмирования, за редким исключением, являются иррациональными числами.

Рациональные и иррациональные числа вместе составляют множество действительных чисел, которое обозначают R.

Приложение 2

Тестовое задание

1. Найдите логарифм по основанию 3 числа 81

1) 2

2) 4

3) 3

4) 1

5) 9

1. Найдите логарифм по основанию 2 числа

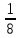
1)

2)

3) -3

4) 3

5) 4

1. Найдите значение выражения

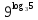
1) 10

2) 25

3) 3

4) 9

5) 5

1. Укажите выражение, значение которого равно 0,5

1)

2)

3)

4) 12

5)

1. Найдите значение выражения

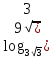
1)

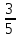
2)

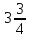
3)

4)

5)

1. Найдите значение выражения

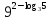
1)

2)

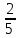
3)

4)

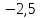
5) 9,5

7. Вычислите )

8. Найдите значение выражения

https://docs.google.com/forms/d/e/1FAIpQLSch5k-BUMKS_VuWSYuA0wymLkw0Kb_gobGIg08uG-AsEotkYQ/viewform?usp=sf_link

Приложение 3

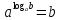
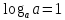
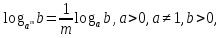
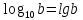
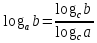
Приложение 4

Фамилия
Имя

	1	2	3	4	5	6
1						
2						
3						
4						
5						

7
8

Приложение 5

	1	2	3	4	5	6
1	 А	 Б	 В	 Г	 Д	 Е
2	 Ж	 З	 И	 Й	 К	 Л
3	 М	 Н	 О	 П	 Р	 С
4	 Т	 У	 Ф	 Х	 Ц	 Ч
5	 Ш	 Щ	 Ь	 Ы	 Ю	 Я

7		БУКВА, КОТОРАЯ В АЛФАВИТЕ СТОИТ ПОД НОМЕРОМ, РАВНЫМ ПОЛУЧЕННОМУ ЧИСЛУ
8		БУКВА В