
Центральная симметрия

Движение плоскости – это отображение плоскости на себя, сохраняющее расстояния.
Если каждой точке плоскости ставится в соответствие какая-то точка этой же плоскости, причем любая точка плоскости оказывается сопоставленной некоторой точке, то говорят, что дано отображение плоскости на себя .

Под движением пространства понимается отображение пространства на себя, при котором любые две точки пространства и отображаются в какие-то точки и так, что .
Движение пространства – это отображение пространства на себя, сохраняющее расстояние между точками.

Фигура называется симметричной относительно точки , если для каждой точки фигуры симметричная ей точка относительно точки также принадлежит этой фигуре. Точка называется центром симметрии фигуры .
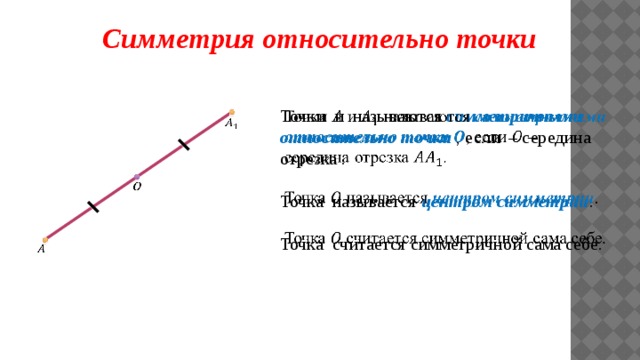
Симметрия относительно точки
Точки и называются симметричными относительно точки , если – середина отрезка .
Точка называется центром симметрии .
Точка считается симметричной сама себе.
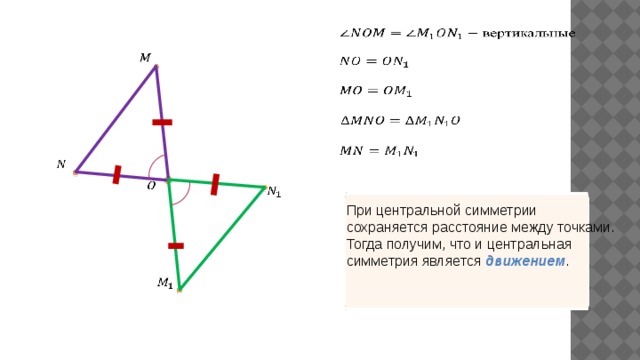
При центральной симметрии сохраняется расстояние между точками. Тогда получим, что и центральная симметрия является движением .
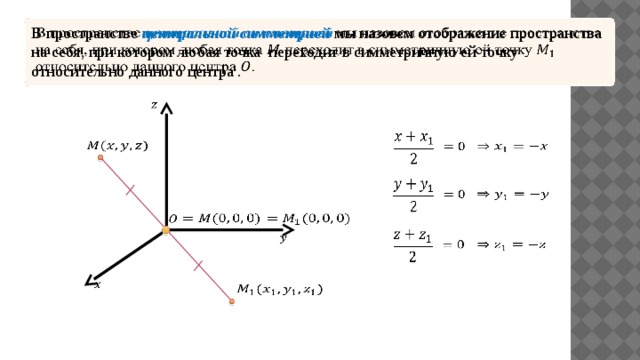
В пространстве центральной симметрией мы назовем отображение пространства на себя, при котором любая точка переходит в симметричную ей точку относительно данного центра .

Расстояние между точками при центральной симметрии в пространстве сохраняется, значит, центральная симметрия в пространстве также является движением , но уже не плоскости, а пространства .

Задача. Найти координаты точек, в которые переходят точки , , при центральной симметрии относительно начала координат.
Решение:
Если точка симметрична точке то справедливы формулы:
.
Точка отобразится в точку .
Точка отобразится в точку .
Точка отобразится в точку .
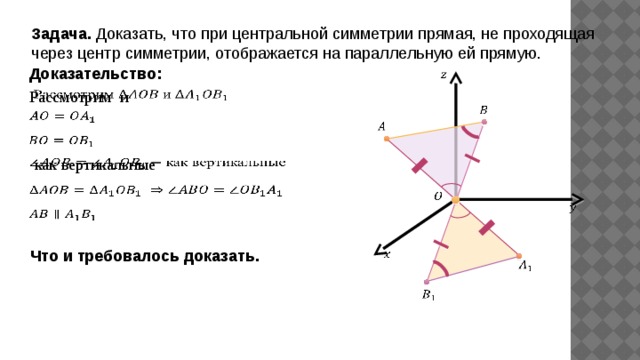
Задача. Доказать, что при центральной симметрии прямая, не проходящая через центр симметрии, отображается на параллельную ей прямую.
Доказательство:
Рассмотрим и
как вертикальные
Что и требовалось доказать.

Спасибо за внимание!





