Теория вероятностей в нашей жизни
Человек всегда стремился предугадать будущее, изменить его. Воспользовавшись теорией вероятностей, вы можете просчитать каковы шансы выигрыша! Взяв формулу и подставив в нее числа, получим процент вероятности события.
Теория вероятностей доказывает, казалось бы, невероятные вещи: машина опасней самолета; кокосы убивают больше человек, чем акулы и др.
Теория вероятностей — раздел математики, изучающий случайные события, случайные величины, их свойства и операции над ними.
Основным понятием теории вероятностей является понятие случайного события. Будем называть событие случайным, если оно относится к случайному опыту (эксперименту), исход которого нельзя точно предсказать.
Например, невозможно предсказать длительность начавшегося или будущего телефонного разговора; нельзя знать, сколько ошибок сделает школьник в предстоящей контрольной работе.
Вероятность и частоты событий.
О случайном событии мы часто не можем сказать заранее, произойдет оно или нет. Но мы можем говорить о шансах наступления этого события.
В теории вероятностей шанс того, что случайное событие произойдет, выражается числом. Это число называют вероятностью случайного события.
Если событие никогда не наступает (его шансы равны нулю), то вероятность этого события полагают равной 0. Такое событие называют невозможным.
Если же событие наступает всегда, его вероятность полагают равной 1. Такое событие называют достоверным.
Вероятности остальных событий – это числа между 0 и 1.
При броске симметричной монеты шансы выпадения орла и решки нужно считать одинаковыми, поскольку монета симметрична. Поэтому вероятности выпадения орла и решки равны между собой. А так как при броске монеты других исходов быть не может, полагают вероятности этих событий равной 0,5.
Классическая вероятность события находится как отношение числа благоприятных исходов к общему числу всех элементарных исходов.
ПРИМЕР: В кармане у Миши было 4 конфеты — «Грильяж», «Белочка», «Коровка» и «Ласточка», а также ключи от квартиры. Вынимая ключи, Миша случайно выронил из кармана 1 конфету. Найти вероятность того, что потерялась конфета «Грильяж».
РЕШЕНИЕ
Конфет «Грильяж» - 1 шт; Всего конфет – 4 шт
Событие А – «Миша вытащил конфету «Грильяж»
.
Станция 1. Нахождение вероятности случайных событий
Задания для решения на станции
В коробке лежат 40 карандашей:17 синих, 9 красных, остальные – желтые. Случайно вытаскивают 1 карандаш. Найти вероятность того, что он окажется желтым.(0,35)
В некотором городе из 5000 появившихся на свет младенцев 2512 мальчиков. Найти частоту рождения девочек в этом городе. Результат округлите до сотых.(0,4976≈0,5)
Из каждой 100 лампочек, поступивших в продажу, в среднем 3 неисправны. Какова вероятность того, что случайно выбранная в магазине лампочка окажется неисправной.(0,03)
Посчитайте сумму результата.(0,88)
ДОП.задания.ПРИЗ ПОБЕДИТЕЛЮ
В фирме такси в данный момент свободно 20 машин: 9 черных, 4 желтых, 7 зеленых. По вызову выехала 1 из машин, случайно оказавшаяся ближе всего к заказчику. Найти вероятность того, что к нему приедет желтое такси.
В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из США, остальные из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найти вероятность того, что спортсменка, выступающая первой, окажется из Китая.
Десятиклассники Петя, Катя, Ваня, Даша и Наташа бросили жребий, кому начинать игру. Найти вероятность, что начинать игру должна будет девочка.
У Вити лежат 12 рублевых, 6 двухрублевых, 4 пятирублевых и 3 десятирублевых монеты. Витя наугад достает из копилки 1 монету. Найти вероятность того, что оставшаяся в копилке сумма составит более 70 рублей.
| Задача 1 | Задача 2 | Задача 3 | Задача 4 |
| 0,5 | 0,25 | 0,6 | 0,72 |
Станция 2. Практическая работа
З
АДАНИЕ 1
Посчитайте количество купленных напитков, результаты занесите в таблицу и вычислите частоту покупки каждого вида кофе.
Частоту покупки данного вида кофе можно найти по формуле (все числа округлите до сотых):
|
| Экспрессо | Американо | Капучино | Латте | итого |
| количество | 137 | 288 | 410 | 165 | 1000 |
| частота | 0,137 | 0,288 | 0,41 | 0,165 |
|
Практическая работа № 1
«Определение частоты выпадения орла при подбрасывании монеты»
Бросьте монету 20 раз и заполните таблицу 1 (воспользуйтесь символом |||| ).
а) Заполните последний столбец таблицы 1, определив частоту выпадения орла по формуле (все числа округлите до сотых):
.
В данном эксперименте знаменатель во всех вычислениях равен 20 – общему числу бросков, а в числитель подставьте числа, полученные в опыте.
Поочередно сообщая свои результаты, заполните таблицу 2 (кроме последнего столбца). Найдите и впишите в ячейку последнего столбца общее количество выпавших орлов, сложив числа, названные отдельными участниками группы.
Найдите общее число бросков и найдите частоту выпадения орла при общем числе бросков.
Таблица 2
| Сторона монеты | Результаты, полученные разными группами учеников | Общее | |||
| №1 | №2 | №3 | |||
| Орел |
|
|
|
| |
| Решка |
|
|
|
| |
| Всего бросков | 20 | 20 | 20 |
| |
| Частота выпадения орла |
|
|
|
| |
В общем частота выпадения орла получилась равной ___________________
Предположите, сколько раз мы можем ожидать выпадение орла, если сделать 10000 бросков монеты?
Ответ_______________________________________________
Практическая работа № 2 «Игральная кость и вероятность»
1 этап.
Давайте проведем эксперимент. Выберите целое число от 1 до 6, которое вам нравится. Посмотрим, что будет происходить при бросании игральной кости. Результаты бросков будем записывать в таблице.
Бросьте игральный кубик 50 раз и заполните таблицу.
2
| Имя участника | Выбранное число | Выпадение загаданного числа | Всего бросков | Частота |
|
|
|
| 50 |
|
|
|
|
| 50 |
|
|
|
|
| 50 |
|
|
|
|
| 50 |
|
| Итого: |
|
|
|
|
2 этап.
а) Заполните последний столбец таблицы 2, используя формулу:
.
3 этап.
а) Предположите, к какому числу должна быть близка частота выпадения любого числа на игральной кости? _______________
Почему?____________________________________________________________
б) Сравните свои экспериментально-полученные результаты с ожидаемым? ______
Станция 3. Решение задач на нахождение вероятности
На этой станции мы рассмотрим некоторые способы нахождения нужного нам количества. Мы решали задачи в простых случаях, но часто количество вариантов приходится просчитывать самим. Рассмотрим несколько примеров.
Задача 1.
Найти вероятность того, что случайно выбранное трехзначное число делится на 49.
Решение:
Количество чисел 
49: 1 (147,196, 243, 292…980)
Количество трехзначных чисел: 
_=900
Р(А) = 
.
Задача 2.
При бросании правильной игральной кости может выпасть любое число от 1 до 6. Какова вероятность, что при бросании кубика не выпадет число 3.
Решение:
Событие А — не выпало число 3 (выпало 1, 2, 4, 5, 6)
Количество вариантов, благоприятных А: 5
Количество всех вариантов: 6
Ответ:__0,83_
Противоположные случайные события
Взаимно противоположные события одновременно произойти не могут, но какое-либо из них происходит обязательно. Поэтому
Задача 3. а) Какова вероятность того, что при двукратном бросании игральной кости во второй раз выпадет не то же число очков, что в первый?
Решение.
Событие А – «оба раза выпали разные цифры».
Количество ? (событию А благоприятствует много элементарных событий). Проще найти вероятность противоположного события:
Событие 
– «оба раза выпадет одно и то же число очков» (11, 22, …,66).
Количество благоприятных для - 6.
Общее количество очков – 
=36
Ответ:___
б) Какова вероятность того, что при двукратном бросании игральной кости сумма очков будет менее 5?
|
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 11 | 12 | 13 | 14 | 15 | 16 |
| 2 | 21 | 22 | 23 | 24 | 25 | 2 |
| 3 | 31 | 32 | 33 | 34 | 35 | 36 |
| 4 | 41 | 42 | 43 | 44 | 45 | 46 |
| 5 | 51 | 52 | 53 | 54 | 55 | 56 |
| 6 | 61 | 62 | 63 | 64 | 65 | 66 |
6
в) Какова вероятность того, что при двукратном бросании игральной кости сумма очков будет равна 6?
Задача 4.
Найти вероятность того, что при четырех бросаниях орел выпадет 2 раза.
Количество благоприятных исходов – __6____
Количество всевозможных исходов – ___16____
| 1 | 2 | 3 | 4 |
|
| 1 | 2 | 3 |
|
|
| 1 | 2 |
| О | О | О | О |
| О | О | О | Р |
| О | О | Р | О |
| О | О | Р | Р |
| О | Р | О | О |
| О | Р | О | Р |
| О | Р | Р | О |
| О | Р | Р | Р |
| Р | О | О | О |
| Р | О | О | Р |
| Р | О | Р | О |
| Р | О | Р | Р |
| Р | Р | О | О |
| Р | Р | О | Р |
| Р | Р | Р | О |
| Р | Р | Р | Р |
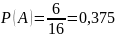
Сделайте опору для решение задач на нахождение вероятности случайных событий. Эта опора пригодится вам на уроках математики для решения экзаменационных задач.
Для этого:
на лист А4 приклейте определения, понятия, примеры и базовую таблицу для решения задач бросание монеты.
Представьте свою работу и получите заслуженный приз!
Удачи!!!
ДЛЯ ОПОРЫ
Вероятности случайных событий
| Невозможное событие Р(А)=0 | Случайное событие
| Достоверное событие Р(А)=1 |
Классическая вероятность события находится как отношение числа благоприятных исходов к общему числу всех элементарных исходов.
Противоположные случайные события
Взаимно противоположные события одновременно произойти не могут, но какое-либо из них происходит обязательно. Поэтому
Задача. Из каждой 100 лампочек, поступивших в продажу, в среднем 3 неисправны. Какова вероятность того, что случайно выбранная в магазине лампочка окажется исправной.
Решение:
Событие А — лампочка исправная
Событие — лампочка неисправная,
Событие А и событие — это противоположные события, значит вероятность события А:
Ответ:___
Задача . Найти вероятность того, что в случайно выбранном двухзначном числе есть одна цифра 5.
Решение:
Двузначные числа , содержащие цифру 5______________________________
_________________________________________________________________
Количество чисел, содержащих цифру 5: ________
Количество двузначных чисел:
=______
Р(А) = 
Ответ:___
| 1 | 2 | 3 | 4 |
|
| 1 | 2 | 3 |
|
|
| 1 | 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Применение теории вероятности на практике
А
теперь давайте обратимся к лотерее. Одна из самых знаменитых и раскрученных лотерей в России – «Спортлото».
Вы заполняете талон лотереи – зачеркиваете 6 чисел из 45. Корешок талона оставляете в пункте покупки. Ждете розыгрыш лотерии, сравниваете свои числа с выпавшими шариками и получаете свой выигрыш.
Попробуем рассчитать вероятность вашего выигрыша.
Во время розыгрыша сначала определяется первое выигрышное число из доступных (у нас — от 1 до 45). Выигравшее число вэтом розыгрыше уже не участвует, иследующее случайное число выбирается из всех чисел, за исключением уже отобранного — то есть, унас останется не 45 вариантов, а 44. И так далее— потом числа будут выбираться из 43, 42, 41и40вариантов.
Мы не станем снуля рассчитывать всё по теории вероятностей, а дадим готовую формулу. Сделайте всего три действия:
45× 44× 43× 42× 41× 40= 5864443200 (почти 6миллиардов)
6× 5× 4× 3× 2× 1= 720
.
Ваш шанс угадать все числа — 1 на более чем 8 миллионов. То есть на одного выигравшего джекпот человека будет 8145060 не выигравших ипотративших (если билет стоит 50рублей) более 400миллионоврублей— на надежду.
Не джекпот, а просто выигрыш— разумноли надеяться
Для того, чтобы быть в плюсе, не обязательно срывать максимальный куш. Скажем, в популярной гослотерее 6из 45, угадав два числа, можно вернуть стоимость билета, аза три— получить втрое больше потраченного. Четыре угаданных числа дадут аж тридцатикратную стоимость билета.
Однако шансы на то, что вы угадаете
два числа — примерно 15 из 100
число комбинаций совпавших чисел – 15
число комбинаций не совпавших чисел – 82251
;
три числа — 22 из 1000
число комбинаций совпавших чисел – 20
число комбинаций не совпавших чисел – 9139
;
четыре числа — 1из 1000.
На каждую тысячу билетов стоимостью 50рублей вы потратите 50000рублей. При этом всреднем вы выиграете 1раз 1500рублей, 21раз— 150рублей и148раз— 50рублей. Всумме ваш выигрыш составит:
1500+ 21× 150+ 148× 50= 12050рублей.
Итого вы потеряете почти 38000рублей. И вообще, разве вы станете класть деньги в банк, если он обещает вам их вернуть с вероятностью 15%?
