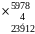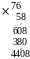ОГЛАВЛЕНИЕ
Введение | 3 |
Основная часть |
|
Глава 1.Теоретическая часть | |
Умножение на пальцах | 4 |
| 4 |
| 4 |
Индийские способы умножения | 5 |
2.1 Простой способ умножения | 5 |
Итальянский способ умножения | 6 |
3.1Умножение способом «Маленикий замок» | 6 |
3.2 Умножение чисел методом «ревность» или «решетчатое умножение» | 6 |
Крестьянский способ умножения | 7 |
Новый способ умножения | 7 |
Глава 2. Практическая часть | 9 |
Заключение | 13 |
Список литературы | 14 |
Вы не сможете выполнить умножения многозначных чисел — хотя бы даже двузначных — если не помните наизусть всех результатов умножения однозначных чисел, т. е. того, что называется таблицей умножения. В разное время разные народы владели разными способами умножения натуральных чисел. Почему же сейчас все народы применяют один способ умножения «столбиком»? чем он так удобен? Почему люди отказались от старых способов умножения в пользу современного? Имеют ли забытые способы умножения право на существование в наше время? Чтобы ответить на эти вопросы я проделал следующую работу:
1. Исследовал информацию о разных способах умножения, которые использовались раньше.;
2. Решил пару примеров всеми изученными способами, чтобы узнать их недостатки и достоинства;
3. Выявил среди них наиболее эффективные;
5. Провел эксперимент;
6. Сделал выводы.
Актуальность: В последнее время навыки устного счета учеников очень низкие. Люди считают, зачем напрягаться, если калькулятор всегда под рукой. В работе приведены разные способы умножение некоторые из них могут облегчить сложные вычисления.
Гипотеза: каким бы ни был способ умножения надо знать таблицу умножения.
Цель проекта: ознакомление с различными способами умножения натуральных чисел, не используемых на уроках, и их применение при вычислениях числовых выражений.
Задачи проекта:
Собрать информацию из различных источников по данной теме для создания проекта;
Проанализировать разные способы умножения.
Провести эксперимент «какой способ быстрей»
Обобщить полученные результаты и сделать выводы;
Защитить проект.
Методы исследования:
Изучение литературы и других источников информации;
Применение разных способов;
Тестирование.
Практическая значимость моего проекта заключается в том, что может быть использована в школе для учащихся младших классов для легкого запоминания таблицы умножения. Данный материал может быть использован во внеурочной деятельности для изучения альтернативных способов умножения или истории развития математики.
Срок работы над проектом - один год.
Основная часть
Глава 1.Теоретическая часть
Умножение на пальцах.
Умножение однозначных чисел, больше 5.
Древнерусский способ умножения на пальцах является одним из наиболее употребительных методов, которым успешно пользовались на протяжении многих столетий российские купцы. Они научились умножать на пальцах однозначные числа от 6 до 9. При этом достаточно было владеть начальными навыками пальцевого счета “единицами”, “парами”, “тройками”, “четверками”, “пятерками” и “десятками”. Пальцы рук здесь служили вспомогательным вычислительным устройством.
Для этого на одной руке вытягивали столько пальцев, на сколько первый множитель превосходит число 5, а на второй делали то же самое для второго множителя. Остальные пальцы загибали. Потом бралось число (суммарное) вытянутых пальцев и умножалось на 10, далее перемножались числа, показывавшие, сколько вытянутух пальцев на руках, а результаты складывались.
Н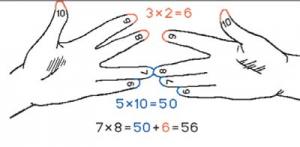 
апример, умножим 8 на 7. В рассмотренном примере будет загнуто 2 и 3 пальца. Если сложить количества загнутых пальцев (2+3=5 – это десятки) и перемножить количеста не загнутых (2•3=6), то получатся соответственно числа десятков и единиц искомого произведения 56 . Так можно вычислять произведение любых однозначных чисел, больше 5.
Умножение на 9.
И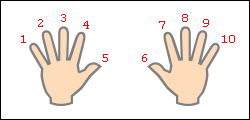 
менно для числа 9 умножение легко воспроизводится «на пальцах». Растопырьте пальцы на обеих руках и поверните руки ладонями от себя. Мысленно присвойте пальцам последовательно числа от 1 до 10, начиная с мизинца левой руки и заканчивая мизинцем правой руки (это изображено на рисунке).
Допустим, хотим умножить 9 на 6. Загибаем палец с номером, равным числу, на которое мы будем умножать девятку. В нашем примере нужно загнуть палец с номером 6. Количество пальцев слева от загнутого пальца показывает нам к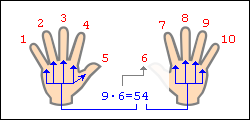 
оличество десятков в ответе, количество пальцев справа — количество единиц. Слева у нас 5 пальцев не загнуто, справа — 4 пальца. Таким образом, 9·6=54. Ниже на рисунке детально показан весь принцип «вычисления».
Еще пример: нужно вычислить 9·8=?. По ходу дела скажем, что в качестве «счетной машинки» не обязательно могут выступать пальцы рук.
| | | | | | | | | |
7 десятков 2 ед. Значит 9·8=72.
Все очень просто.
Индийский способ умножения.
1. Простой способ умножения.
Самый ценный вклад в сокровищницу математических знаний был совершен в Индии. Индусы предложили употребляемый нами способ записи чисел при помощи десяти знаков: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Они придумали очень простой способ умножения. Они умножение выполняли, начиная со старшего разряда, и записывали неполные произведения как раз над множимым, поразрядно. При этом сразу был виден старший разряд полного произведения и, кроме того, исключался пропуск какой-либо цифры. Знак умножения еще не был известен, поэтому между множителями они оставляли небольшое расстояние.
Например, умножим их способом 537 на 6:
537∙6 (5 ∙ 6 =30) 30 | 30 |
537∙6 (300 + 3 ∙ 6 = 318) | 318
|
537∙6 (3180 +7 ∙ 6 = 3222) | 3222 |
Умножение крестиком
В одной старинной русской рукописи описывается интересный прием «умножения крестиком», применявшийся еще в древней Индии под названием «молниеносного».
Пример: 24 х 32 = 768 Последовательно производим следующие действия:
2 4 X
|
|
Ответ – 768.
Умножение способом «МАЛЕНЬКИЙ ЗАМОК».
И 
тальянский математик Лука Пачоли в своём трактате «Сумма знаний по арифметике, отношениям и пропорциональности»(1494 г.) приводит восемь различных методов умножения. Первый из них носит название «Маленький замок», а второй не менее романтичное название «Ревность или решетчатое умножение».
Цифры одного из чисел, на примере это нижний множитель, начиная со старшего разряда, поочередно умножаются на нижнее число и записываются в столбик с добавлением нужного числа нулей. Затем результаты складываются.
Умножение чисел методом «ревность» или «решётчатое умножение».
С 
начала рисуется прямоугольник, разделённый на квадраты, причём размеры сторон прямоугольника соответствуют числу десятичных знаков у множимого и множителя. Затем квадратные клетки, делятся по диагонали, и «…получается картинка, похожая на решётчатые ставни-жалюзи, — пишет Пачоли. – Такие ставни вешались на окна венецианских домов, мешая уличным прохожим видеть, сидящих у окон дам и монахинь».
С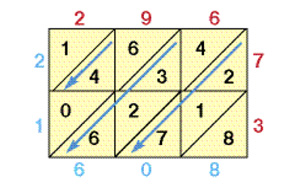
уть этого нехитрого способа умножения поясним на примере: вычислим произведение 296 × 73. Начнём с того, что нарисуем таблицу с квадратными клетками, в которой будет три столбца и две строки, — по количеству цифр в множителях. Разделим клетки пополам по диагонали. Над таблицей запишем число 296, а с правой стороны вертикально — число 73. Перемножим каждую цифру первого числа с каждой цифрой второго и запишем произведения в соответствующие клетки, располагая десятки над диагональю, а единицы под ней. Цифры искомого произведения получим сложением цифр в косых полосах. При этом будем двигаться по часовой стрелке, начиная с правой нижней клетки: 8, 2 + 1 + 7 и т.д. Запишем результаты под таблицей, а также слева от неё. (Если при сложении получится двузначная сумма, укажем только единицы, а десятки прибавим к сумме цифр из следующей полосы.)
Ответ: 21608.
Крестьянский способ умножения.
Самым, на мой взгляд, «родным» и легким способом умножения является способ, который употребляли русские крестьяне. Этот прием вообще не требует знания таблицы умножения дальше числа 2.
С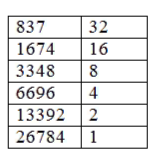
ущность его в том, что умножение любых двух чисел сводится к ряду последовательных делений одного числа пополам при одновременном удвоении другого числа. Деление пополам продолжают до тех пор, пока в частном не получится 1, параллельно удваивая другое число. Последнее удвоенное число и дает искомый результат.
.
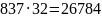В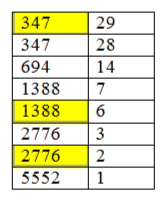
случае нечетного числа надо откинуть единицу и делить остаток пополам; но зато к последнему числу правого столбца нужно будет прибавить все те числа этого столбца, которые стоят против нечетных чисел левого столбца: сумма и будет искомым произведением
Рассмотрим пример:
347 ∙ 29 = 347 ∙ (28 + 1) =347 ∙ 28 +347 =1388 ∙ (6+1)+347 =
= 1388 ∙ 6+1388+347 =2776 ∙ (2+1) +1388+347 = 5552+2776+1388+347=10063
Если вы поняли принцип работы этим способом, запись можно сократить:
347 ∙ 29 = 5552+2776+1388+347=10063
Новый способ умножения.
И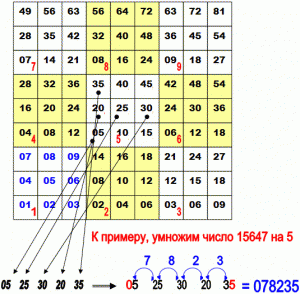 
нтересен новый способ умножения, о котором недавно появились сообщения. Изобретатель новой системы устного счёта кандидат философских наук Василий Оконешников утверждает, что человек способен запоминать огромный запас информации, главное – как эту информацию расположить. По мнению самого учёного, наиболее выигрышной в этом отношении является девятеричная система – все данные просто располагают в девяти ячейках, расположенных, как кнопочки на калькуляторе.
Считать по такой таблице очень просто. К примеру, умножим число 15647 на 5. В части таблицы, соответствующей пятёрке, выбираем числа, соответствующие цифрам числа по порядку: единице, пятёрке, шестёрке, четвёрке и семёрке. Получаем: 05 25 30 20 35
Левую цифру (в нашем примере — ноль) оставляем без изменений, а следующие цифры складываем попарно: пятёрку с двойкой, пятёрку с тройкой, ноль с двойкой, ноль с тройкой. Последняя цифра также без изменений.
В итоге получаем: 078235. Число 78235 и есть результат умножения.
Если же при сложении двух цифр получается число, превосходящее девять, то его первая цифра прибавляется к предыдущей цифре результата, а вторая пишется на «своё» место.
Глава 2. Практическая часть
Изучая различные способы умножения, я пробовал умножать ими различные числа (однозначные и многозначные, четные и нечетные, с использованием чисел меньше 5 и больше). В процессе анализа способов, выделил их преимущества и недостатки.
| Название способа | Преимущества | Недостатка |
Умножение на пальцах | Умножение однозначных чисел, больше 5 | Легкий и быстрый способ | Узкая область для применения (10 примеров: 6∙6, 6∙7, 6∙8, 6∙9, 7∙7, 7∙8, 7∙9, 8∙8, 8∙9, 9∙9) |
Умножение на 9 | - Не требует никаких специальных знаний - Легко запомнить | Применим только при умножении на 9 | |
Индийский способ умножения | Простой способ умножения | - Легкий и быстрый способ - Не надо много писать | Подходить только для умножения многозначного числа на однозначное число |
Умножение крестиком
| - Легкий и быстрый способ - запись сводится к минимуму | Применим только для двух двузначных чисел | |
| «Маленький замок» | - Самого начала определяются цифры старших разрядов, а это бывает важно, если требуется быстро оценить величину. - Универсальный способ, для любых чисел. | Требуется запись |
«Ревность» или «решётчатое умножение»
| - Простое и надёжнее умножение. - Работать приходится только с однозначными и двузначными числами, а ими легко оперировать в уме. - Не требуется запоминать промежуточные результаты и следить за тем, в каком порядке их записывать. Память разгружается, а внимание сохраняется, поэтому вероятность ошибки уменьшается. К тому же способ решётки позволяет быстрее получить результат. Освоив его, вы сможете убедиться в этом сами. | Требуется табличка-заготовка | |
| Крестьянский способ умножения | - Самый легкий способ умножения для четных чисел. - Вообще не требует знания таблицы умножения дальше числа 2. | - Требуется запись последовательности чисел В случаях с нечетными числами, требует особой внимательности, можно потерять остаток |
| Новый способ умножения | - Легкий и быстрый способ - Не надо много писать | Подходит для умножения на однозначное число |
Первые два способа могут нам помочь только в запоминании таблицы умножения, причем простота способа «умножение для чисел больше 5» очень сомнительна. На мой взгляд, проще запомнить 10 примеров, чем последовательность действий этого способа.
Индийские способы просты, но в них нет универсальности – заменить ими наш «столбик» можно только в частных случаях. Сравним это способы с умножением в «столбик»
5978∙4 20
200+36 2360+28=388 23880+32=3912 | - используется навык сложения - необходимо записать или выполнить в уме три действия сложения | | - использует навык сложения - необходимо каждый раз запоминать и прибавлять число десятков | |
7 6 х 5 8 | 8∙6=48 7∙8+6∙5+4=90 5∙7+9=44 4408
| - используется знание таблицы умножения; - использует навык сложения; - необходимо каждый раз запоминать и прибавлять число десятков. | | - используется знание таблицы умножения; - использует навык сложения; - необходимо каждый раз запоминать и прибавлять число десятков; - не забыть сместить число при умножении на десятки. |
Способ умножения «Маленький замок», описанный итальянским математиком очень похож на наш современный способ умножения «столбиком». На мой взгляд, эта форма записи удобнее, чем наш столбик, т.к. не надо смещать при умножении на десятки, сотни и т.д.; сразу виден старший разряд.
Способ умножения «Ревность» или «решётчатое умножение» очень прост. Не смотря на то, что необходимо начертить табличку для вычисления, но пользоваться им предельно просто и освоит любой двоишник!
Еще один очень простой способ умножения – это крестьянский. Этот способ подойдет для тех, кто так и не смог запомнить таблицу умножения. Писать надо многовато, но умея умножать на 2 и отличая четное число от нечетного, ты сможешь вычислить любой пример.
|
| ||||||||
| Помогает в запоминании таблицы умножения | Подходит для умножения любого числа на однозначное число | Подходит для умножения двузначных чисел | Подходит для умножения любых чисел | Не требует знания таблицы умножения | Не требует больших записей | Не требуются специальные средства |
| |
Умножение однозначных чисел, больше 5 | + | | | | | + | + |
| |
Умножение на 9 | + | | | | | + | + |
| |
Простой способ умножения | | + | | | | + | + |
| |
Умножение крестиком
| | | + | | | + | + |
| |
«Маленький замок» | | | | + | | | + |
| |
«Ревность» или «решётчатое умножение» | | | | + | | + | + |
| |
Крестьянский способ умножения | | | | + | + | | + |
| |
Новый способ умножения | | + | | | + | | |
| |
Заключение
Работая над индивидуальным проектом, я узнал, что существует порядка 30 различных, забавных и интересных способов умножения. Некоторыми в различных странах пользуются до сих пор. Я выбрал для себя некоторые интересные способы. Но не все способы удобны в использовании, особенно при умножении многозначных чисел. Для удобства анализа удобства того или иного способа, собрал информацию в таблицы. Цель моего проекта достигнута полностью.
Для реализации поставленной цели мною были достигнуты задачи:
собрал информацию из различных источников по данной теме для создания проекта;
проанализировал разные способы умножения;
провел эксперимент «какой способ удобнее и быстрее»;
обобщил полученные результаты и сделать выводы.
Продуктом моего индивидуального проекта является буклет, в котором я собрал наиболее интересные способы умножения. Применение различных способов умножения позволяет повысить интерес к предмету «математика», позволяет каждому ученику найти свой способ.
Список литературы
Олехник С.Н., Нестеренко Ю.В., Потапов М.К. Старинные занимательные задачи». – М.: Наука. Главная редакция физико-математической литературы, 1985. – 160.
Перельман Я.И.Занимательная арифметика, - М.: АО «Столетие», 1994. -176 с.
Энциклопедия я познаю мир. Математика. – М.: Астрель Ермак, 2004.- 368 с.
https://nsportal.ru/nachalnaya-shkola/matematika/2015/02/14/indiyskiy-sposob-umnozheniya
http://iteach.vspu.ru/07-2017/14733/
