
Скрещивающиеся прямые

a
b

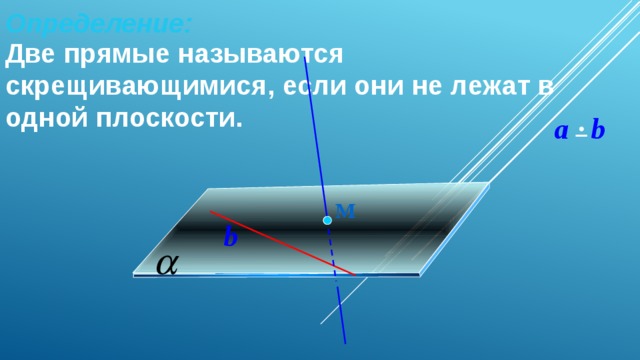
Определение:
Две прямые называются скрещивающимися, если они не лежат в одной плоскости.
a b
М
b

Наглядное представление о скрещивающихся прямых дают две дороги, одна из которых проходит по эстакаде, а другая под эстакадой.

Теорема: Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).
Доказательство Рассмотрим прямую AB лежащую в плоскости и прямую CD , которая пересекает плоскoсть в точке D , не лежащей на прямой AB .
1. Допустим, что прямые AB и CD всё-таки лежат в одной плоскости. 2. Значит эта плоскость идёт через прямую AB и точку D , то есть она совпадает с плоскостью α. 3. Это противоречит условиям теоремы, что прямая CD не находится в плоскости α , а пересекает её. Теорема доказана.
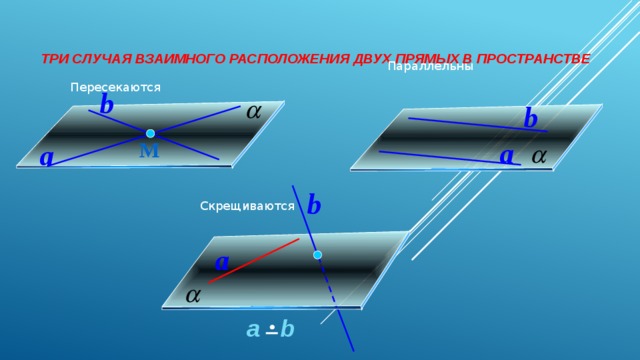
Три случая взаимного расположения двух прямых в пространстве
Параллельны
Пересекаются
b
b
a
М
a
b
Скрещиваются
a
а b

Теорема о скрещивающихся прямых
Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.
Доказательство Рассмотрим скрещивающиеся прямые AB и CD . 1. Через точку D можно провести прямую DE параллельную AB . 2. Через пересекающиеся прямые CD и DE можно провести плоскость α 3. Так как прямая А B не лежит в этой плоскости и параллельна прямой DE , то она параллельна плоскости.
4. Эта плоскость единственная, так как любая другая плоскость, проходящая через CD , будет пересекаться с DE и AB , которая ей параллельна. Теорема доказана.

Спасибо за внимание !





