
Решение уравнений и неравенств с параметром

Линейные уравнения с параметром
- линейное уравнение
- линейное уравнение с параметром
- функция соответствующая линейному уравнению
x – любое
y
y
9
нет решений
единственное решение
0
x
-2
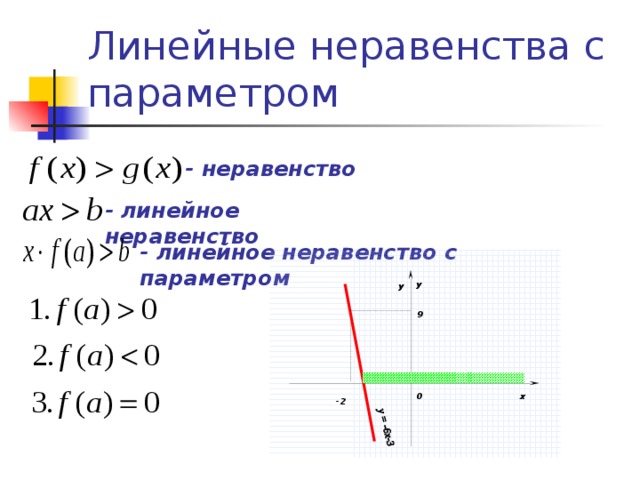
Линейные неравенства с параметром
- неравенство
- линейное неравенство
- линейное неравенство с параметром
y
y
9
0
x
-2

Системы линейных уравнений с параметром
- система
линейных уравнений
y
y
y
y
x
0
x
x
x

Квадратные уравнения с параметром
Теорема 1
Теорема 2
Теорема 3
Теорема 4
Теорема 5
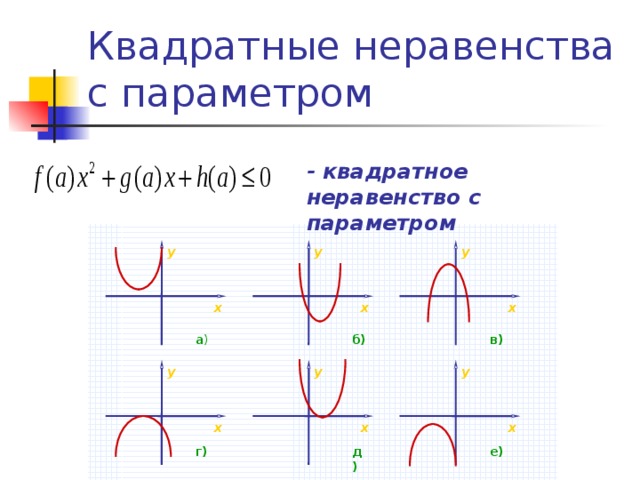
Квадратные неравенства с параметром
- квадратное неравенство с параметром
y
y
y
x
x
x
а )
в)
б)
y
y
y
x
x
x
г)
д)
е)

Дробно-рациональные уравнения с параметром
- дробно-рациональное уравнение
- дробно-рациональное уравнение с параметром
- Перенести все члены уравнения в одну часть.
- Преобразовать эту часть уравнения к виду алгебраической дроби .
- Решить уравнение P(x)=0 .
- Для каждого корня уравнения P(x)=0 сделать проверку: удовлетворяет оно условию Q(x) ≠0 или нет. Если да, то это – корень уравнения; если нет, то это – посторонний корень и в ответ его включать не следует.

Спасибо за внимание!





