Решение тригонометрических уравнений

Разработка урока по алгебре и началам математического анализа «Способы решения тригонометрических уравнений»

Цели.

1. Организовать деятельность учащихся по самостоятельному применению комплекса знаний и способов действий.

2. Включить усвоенные знания и способы действий учащихся по данной теме в общую систему их знаний и способов действий.

3. Продолжить формирование у учащихся адекватного представления о степени своей обученности.

Тип урока. Урок комплексного применения знаний.

Форма учебного занятия. Урок – семинар.

Технология. Традиционная в сочетании с элементами адаптивного и проблемного обучения.

Эпиграф урока. « Находите время для работы – это источник успеха».

Ход урока.

I. Организация начала занятия.

Проверить готовность класса к уроку.

II. Подготовка учащихся к активной учебно – познавательной деятельности на основном этапе урока.

II₁. Мотивация учения.

Сегодня на уроке мы продолжим рассматривать способы решения тригонометрических уравнений. Прежде чем приступить к основному этапу урока просмотрим презентацию «История происхождения тригонометрических терминов», подготовленную Комаровой Анной.

II₂. Актуализация комплекса знаний.

Выполнение теста со взаимопроверкой.

Учащиеся выполняют тест по вариантам, ответы заносят в таблицу, обмениваются и проверяют правильность выполнения заданий. Баллы заносят в оценочный лист.

Вариант
1	2	3	4	5

III. Основной этап урока.

Разбор методов решения тригонометрических уравнений по плану.

1. Метод понижения степени.

2. Метод универсальной подстановки.

3. Использование ограничений функций при решении.

4. Уравнения, содержащие знак модуля или корня.

Учащимся предлагалось дома подобрать и решить уравнения данными способами. По желанию они выходят к доске и объясняют свое решение.

1. sin⁴x + cos⁴x = ,

( + ( =

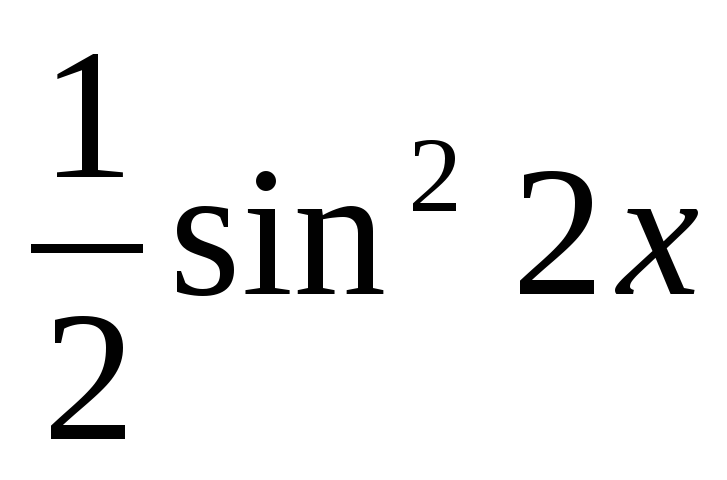1 + cos²2x = sin²2x,

2cos² 2x = 0,

cos2x = 0,

x =

Ответ:

1. 2cos2x + 2tg²x = 5,

О.Д.З. х

2х = 5,

2 – 2tg²x + 2tg²x + 2tg⁴x = 5 + 5tg²x.

Пусть tgx = t, тогда 2t⁴ – 5t² – 3 = 0,откуда t = или t = -.

tgx = или tgx = -,

x =

Ответ:

1. 1) tg² 3x = cos2x – 1,

tg² 3x = - 2sin²x,

Решение 1 – ого уравнения: x = .

Решение 2 – ого уравнения: x =

Отсюда их общее решение: x =

Ответ:

2) sinx + 3cos4x = 4,

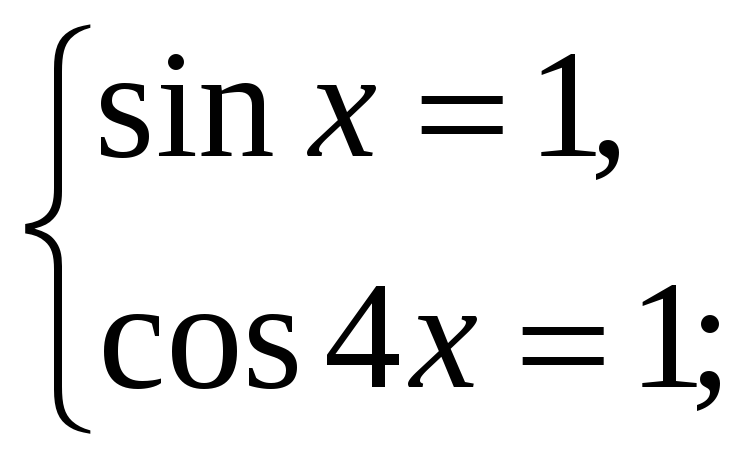
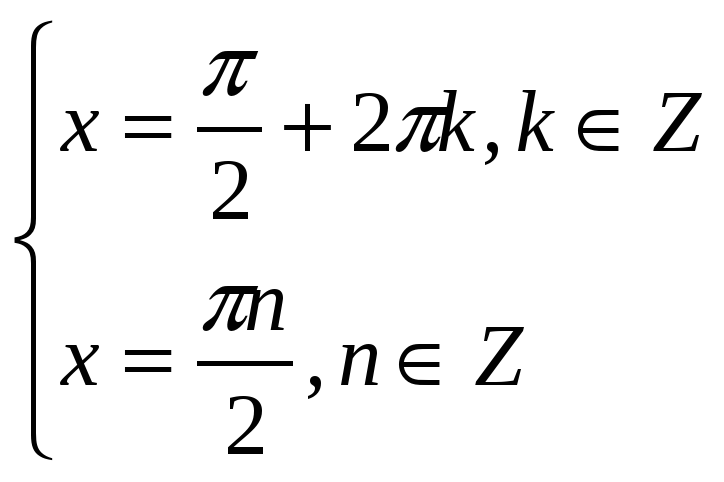x =

Ответ:

3) sinx + cos4x = -2. Нет решений.

4. 1)

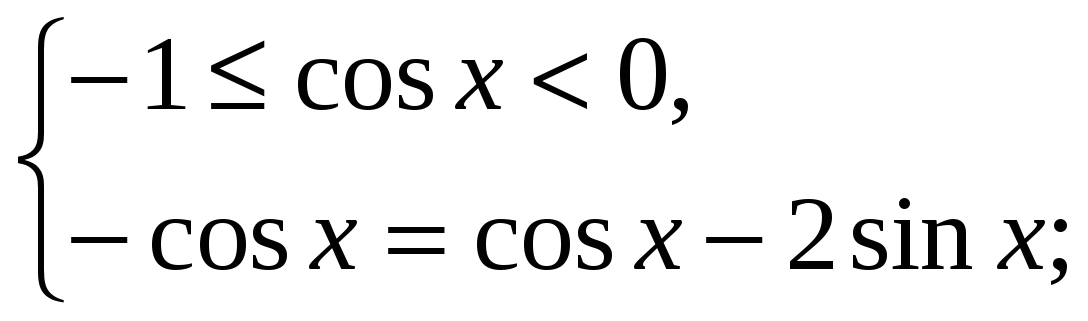
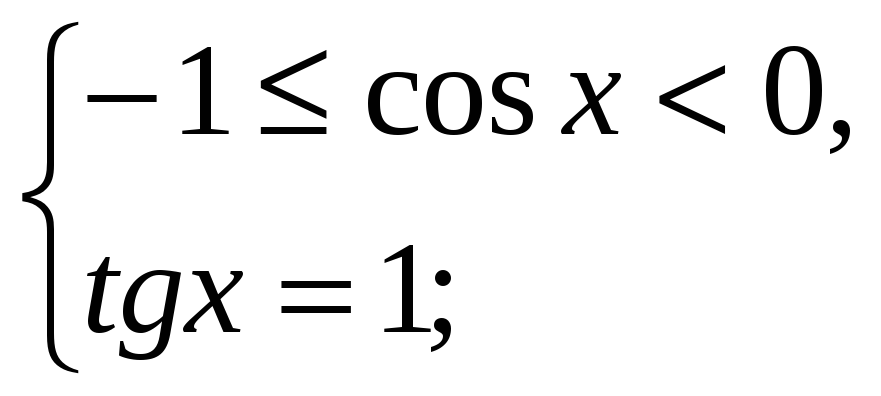
x =

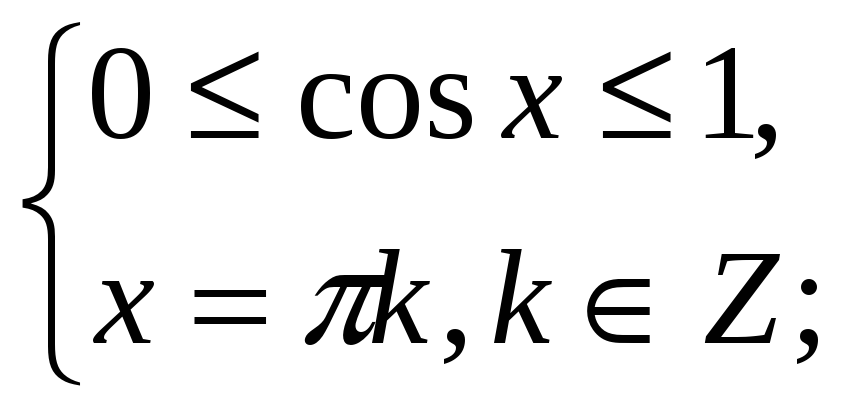x=2

Ответ: 2

2) .

2cos²x + 5cosx – 3 = 0.

Пусть сosx = t, где тогда решим уравнение 2t² +5t - 3=0,

t = -3; t = 0,5.

Cosx = 0,5,

x =

Учитывая, что sinx , получим

x = -

Ответ: -

IV. Cамостоятельное применение знаний.

Учащиеся разбиты на группы. Им предлагается обсудить выбор способа решения тригонометрических уравнений, решить их, проверить и оценить.

Перед ними таблица.

Оцените работу группы по каждому заданию по следующим критериям:

• ответ совпадает полностью - полное количество

баллов, указанных в скобках к заданию;

• ответ совпадает частично - половина указанных

баллов;

• ответ не совпадает - 0 баллов.

I.

1. cos²6x – sin²3x – 1 = 0. (2 балла)

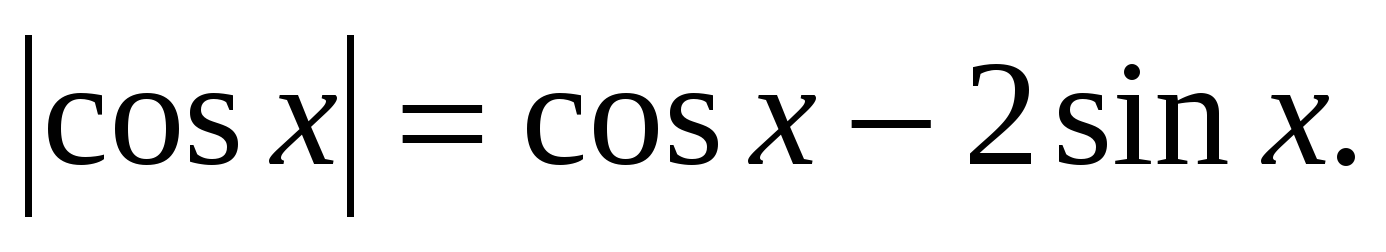2. (2 балла)

II.

1. sin²⁰⁰⁶x + cos²⁰⁰⁶x = 1. (2 балла)

2. sinx + tg 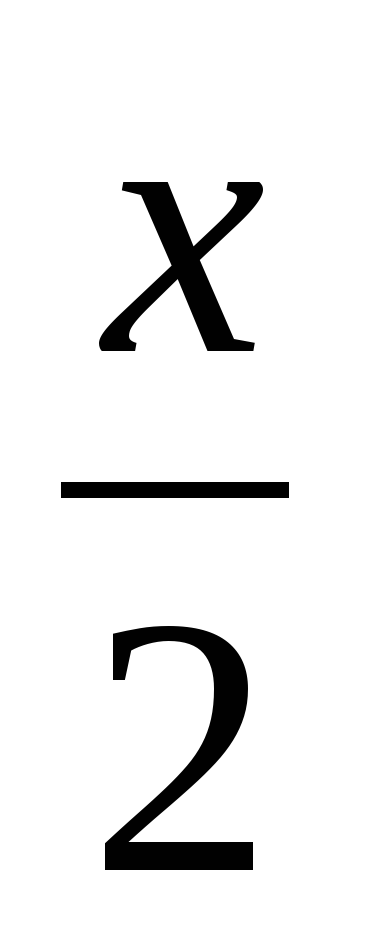= 0. (2 балла)

III.

1. Sin4x = 3cos2x. (1 балл)

2. 1+ сosx + tg 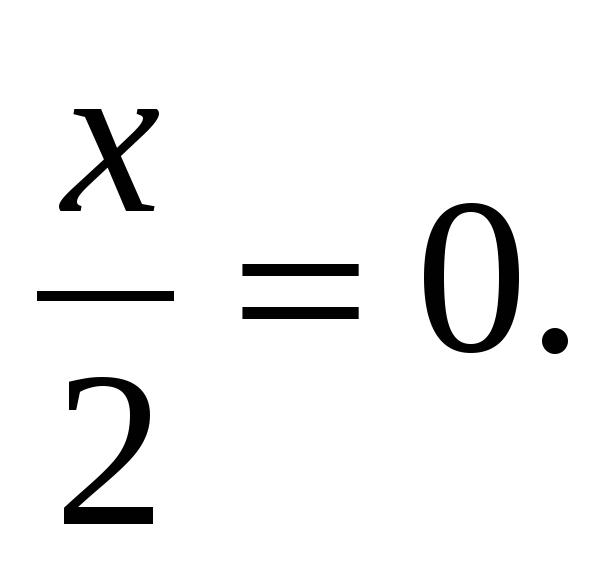(2 балла)

IV.

1. cos²x = sinx 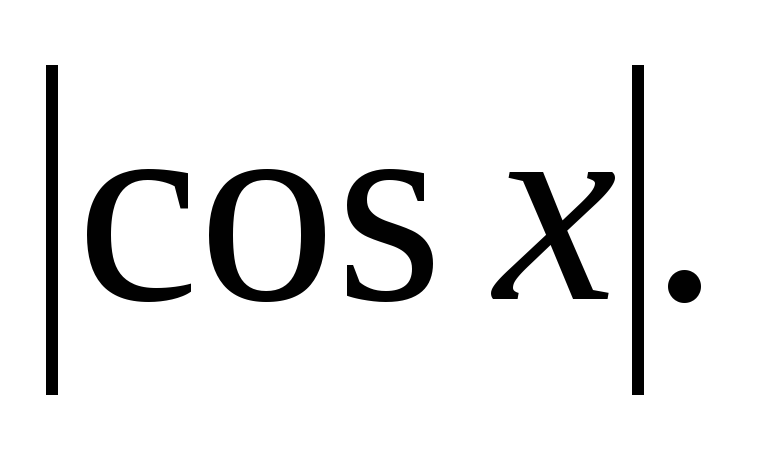(2 балла)

2. sin²x + sin²2x – sin²3x – sin²4x = 0. (2 балла)

V.

1) sin2x + tgx = 2. (2 балла)

2) sin²x + ( 2 балла)

VI.

1. 6 sin²x + 2 sin²2x = 5. (2 балла)

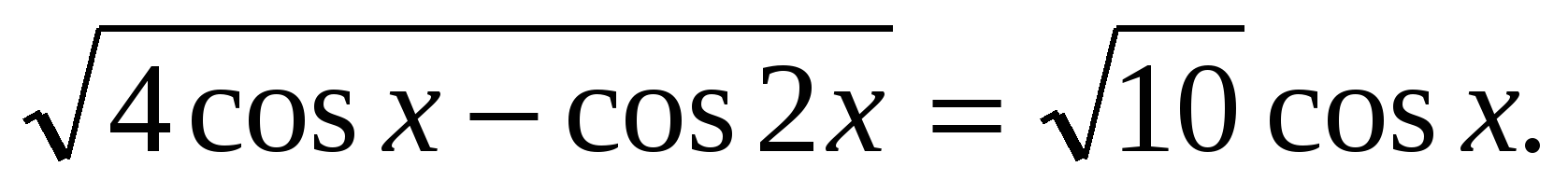2. (2 балла)

Результаты работы ученики заносят в свою оценочную таблицу.

Фамилия, имя Этапы Кто оценивает Кол-во баллов Тест Работа у доски Работа в группах Итого Оценка

V. Подведение урока - семинара.

1. Выставление оценок отвечающим у доски; учащимся, защитившим свою работу в группах; учащимся, решившим дополнительные уравнения.

2. Выставляются и комментируются баллы за тест, за групповую работу, за домашнюю работу в рейтинговую систему оценки знаний.

3. Подведя итог урока, хочется вернуться к эпиграфу урока «Находите время для работы – это источник успеха!».

VII. Рефлексия деятельности.

VIII. Информация о домашнем задании.

Подберите и решите тригонометрические уравнения следующими способами:

1. С помощью вспомогательного угла.

2. Уравнения вида Р(sinx + cosx, sinxcosx) = 0.

3. Уравнения, содержащие два корня.