Разбор задания 3 из ОГЭ-2023 "Формальные описания реальных объектов и процессов.docx"

1. Формальные описания реальных объектов и процессов

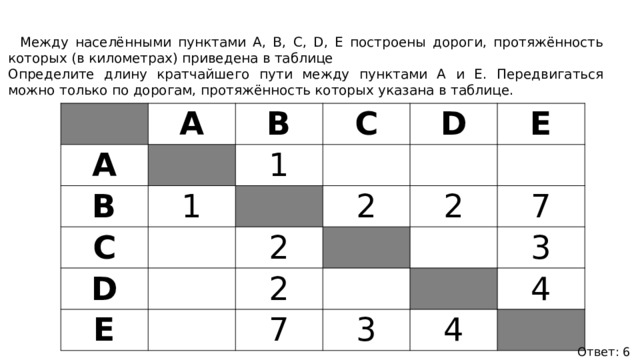
1. Между населёнными пунк­та­ми А, В, С, D, Е по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых (в ки­ло­мет­рах) при­ве­де­на в таб­ли­це:

	A	B	C	D	E
A		1
B	1		2	2	7
C		2			3
D		2			4
E		7	3	4

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми А и E. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, про­тяжённость ко­то­рых ука­за­на в таб­ли­це.  

1) 5

2) 6

3) 7

4) 8

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из A в E и вы­бе­рем самый ко­рот­кий.

 

Из пунк­та A можно по­пасть в пункт B.

Из пунк­та B можно по­пасть в пунк­ты C, D, E.

Из пунк­та C можно по­пасть в пункт E.

Из пунк­та D можно по­пасть в пункт E.

 

A—B: длина марш­ру­та 1 км.

A—B—C—E: длина марш­ру­та 6 км.

A—B—D—E: длина марш­ру­та 7 км.

A—B—E: длина марш­ру­та 8 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

Ответ: 2

3

2

Источник: ГИА по информатике 31.05.2013. Основная волна. Центр, Урал. Вариант 1301.

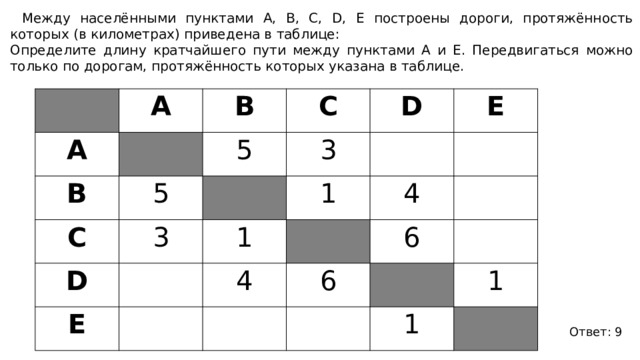
2. Между населёнными пунк­та­ми А, В, С, D, Е по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых (в ки­ло­мет­рах) при­ве­де­на в таб­ли­це: 

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми А и E. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, про­тяжённость ко­то­рых ука­за­на в таб­ли­це.  

1) 7

2) 8

3) 9

4) 10

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из A в E и вы­бе­рем самый ко­рот­кий.

 

Из пунк­та A можно по­пасть в пунк­ты B, С.

Из пунк­та B можно по­пасть в пунк­ты C, D.

Из пунк­та C можно по­пасть в пункт D.

Из пунк­та D можно по­пасть в пункт E.

 

A—B—C—D—E: длина марш­ру­та 13 км.

A—B—D—E: длина марш­ру­та 10 км.

A—C—D—E: длина марш­ру­та 10 км.

A—C—B—D—E: длина марш­ру­та 9 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 3.

Ответ: 3

23

3

Источник: ГИА по информатике 31.05.2013. Основная волна. Центр, Урал. Вариант 1302.

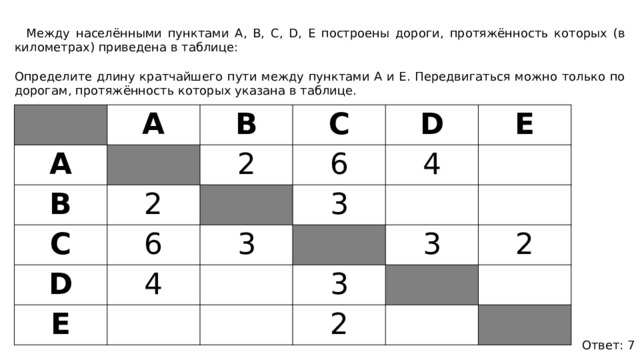
3. Между населёнными пунк­та­ми А, В, С, D, Е по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых (в ки­ло­мет­рах) при­ве­де­на в таб­ли­це: 

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми А и E. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, про­тяжённость ко­то­рых ука­за­на в таб­ли­це.  

1) 9

2) 10

3) 11

4) 12

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из A в E и вы­бе­рем самый ко­рот­кий.

 

Из пунк­та A можно по­пасть в пунк­ты B, С.

Из пунк­та B можно по­пасть в пунк­ты C, E.

Из пунк­та C можно по­пасть в пункт D.

Из пунк­та D можно по­пасть в пункт E.

 

A—B—C—D—E: длина марш­ру­та 10 км.

A—B—E: длина марш­ру­та 11 км.

A—C—D—E: длина марш­ру­та 12 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

Ответ: 2

43

2

Источник: ГИА по информатике 31.05.2013. Основная волна. Центр, Урал. Вариант 1303.

4. Между населёнными пунк­та­ми А, В, С, D, Е по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых (в ки­ло­мет­рах) при­ве­де­на в таб­ли­це: 

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми А и E. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, про­тяжённость ко­то­рых ука­за­на в таб­ли­це.  

1) 5

2) 6

3) 7

4) 9

2. Формальные описания реальных объектов и процессов

1По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из A в E и вы­бе­рем самый ко­рот­кий.

 

Из пунк­та A можно по­пасть в пункт B.

Из пунк­та B можно по­пасть в пунк­ты C, D, E.

Из пунк­та C можно по­пасть в пункт E.

Из пунк­та D можно по­пасть в пункт E.

 

A—B—C—E: длина марш­ру­та 9 км.

A—B—E: длина марш­ру­та 9 км.

A—B—D—E: длина марш­ру­та 7 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 3.

Ответ: 3

63

3

Источник: ГИА по информатике 31.05.2013. Основная волна. Центр, Урал. Вариант 1304.

. Между населёнными пунк­та­ми А, В, С, D, Е по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых (в ки­ло­мет­рах) при­ве­де­на в таб­ли­це: 

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми А и E. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, про­тяжённость ко­то­рых ука­за­на в таб­ли­це.  

1) 8

2) 9

3) 10

4) 11

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из A в E и вы­бе­рем самый ко­рот­кий.

 

Из пунк­та A можно по­пасть в пунк­ты B, С.

Из пунк­та B можно по­пасть в пунк­ты C, D.

Из пунк­та C можно по­пасть в пункт D.

Из пунк­та D можно по­пасть в пункт E.

 

A—B—C—D—E: длина марш­ру­та 9 км.

A—B—D—E: длина марш­ру­та 10 км.

A—C—D—E: длина марш­ру­та 11 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

Ответ: 2

83

2

Источник: ГИА по информатике 31.05.2013. Основная волна. Сибирь, Даль­ний Восток. Вариант 1305.

2. Между населёнными пунк­та­ми А, В, С, D, Е по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых (в ки­ло­мет­рах) при­ве­де­на в таб­ли­це: 

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми А и E. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, про­тяжённость ко­то­рых ука­за­на в таб­ли­це.  

1) 9

2) 10

3) 11

4) 12

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из A в E и вы­бе­рем самый ко­рот­кий.

 

Из пунк­та A можно по­пасть в пунк­ты B, С.

Из пунк­та B можно по­пасть в пунк­ты C, E.

Из пунк­та C можно по­пасть в пункт D.

Из пунк­та D можно по­пасть в пункт E.

 

A—B—C—D—E: длина марш­ру­та 17 км.

A—B—E: длина марш­ру­та 11 км.

A—C—D—E: длина марш­ру­та 12 км.

A—C—B—E: длина марш­ру­та 10 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

Ответ: 2

103

2

Источник: ГИА по информатике 31.05.2013. Основная волна. Сибирь, Даль­ний Восток. Вариант 1306.

3. Между населёнными пунк­та­ми А, В, С, D, Е по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых (в ки­ло­мет­рах) при­ве­де­на в таб­ли­це: 

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми А и E. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, про­тяжённость ко­то­рых ука­за­на в таб­ли­це.  

1) 9

2) 8

3) 7

4) 6

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из A в E и вы­бе­рем самый ко­рот­кий.

 

Из пунк­та A можно по­пасть в пункт B.

Из пунк­та B можно по­пасть в пунк­ты C, D, E.

Из пунк­та C можно по­пасть в пункт E.

Из пунк­та D можно по­пасть в пункт E.

 

A—B—C—E: длина марш­ру­та 7 км.

A—B—D—E: длина марш­ру­та 8 км.

A—B—E: длина марш­ру­та 9 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 3.

Ответ: 3

123

3

Источник: ГИА по информатике 31.05.2013. Основная волна. Сибирь, Даль­ний Восток. Вариант 1307.

4. Между населёнными пунк­та­ми А, В, С, D, Е по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых (в ки­ло­мет­рах) при­ве­де­на в таб­ли­це: 

 Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми А и E. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, про­тяжённость ко­то­рых ука­за­на в таб­ли­це.  

1) 4

2) 5

3) 6

4) 7

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из A в E и вы­бе­рем самый ко­рот­кий.

 

Из пунк­та A можно по­пасть в пунк­ты B, C, D.

Из пунк­та B можно по­пасть в пункт C.

Из пунк­та C можно по­пасть в пунк­ты D, E.

 

A—B—C—E: длина марш­ру­та 7 км.

A—С—E: длина марш­ру­та 7 км.

A—D—C—E: длина марш­ру­та 6 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 3.

Ответ: 3

143

3

Источник: ГИА по информатике 31.05.2013. Основная волна. Вариант 1308.

5. Между населёнными пунк­та­ми А, В, С, D, Е по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых (в ки­ло­мет­рах) при­ве­де­на в таб­ли­це:

 

 Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми А и E. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, про­тяжённость ко­то­рых ука­за­на в таб­ли­це.  

1) 6

2) 7

3) 8

4) 9

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из A в E и вы­бе­рем самый ко­рот­кий.

 

Из пунк­та A можно по­пасть в пунк­ты B, D.

Из пунк­та B можно по­пасть в пунк­ты C, D.

Из пунк­та C можно по­пасть в пунк­ты D, E.

 

A—B—C—E: длина марш­ру­та 7 км.

A—D—B—C—E: длина марш­ру­та 9 км.

A—D—C—E: длина марш­ру­та 6 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 1.

Ответ: 1

163

1

Источник: ГИА по информатике 31.05.2013. Основная волна. Вариант 1309.

10. За­да­ние 3 № 183. Между населёнными пунк­та­ми А, В, С, D, Е по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых (в ки­ло­мет­рах) при­ве­де­на в таб­ли­це:

 

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми А и E. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, про­тяжённость ко­то­рых ука­за­на в таб­ли­це.

 

1) 5

2) 6

3) 7

4) 8

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из A в E и вы­бе­рем самый ко­рот­кий.

 

Из пунк­та A можно по­пасть в пунк­ты B, C.

Из пунк­та B можно по­пасть в пунк­ты D, E.

Из пунк­та C можно по­пасть в пункт D.

Из пунк­та D можно по­пасть в пункт E.

 

A—B—E: длина марш­ру­та 7 км.

A—B—D—E: длина марш­ру­та 6 км.

A—C—D—E: длина марш­ру­та 8 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

Ответ: 2

183

2

Источник: ГИА по информатике 31.05.2013. Основная волна. Вариант 1310.

11. За­да­ние 3 № 203. Между населёнными пунк­та­ми А, В, С, D, Е по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых (в ки­ло­мет­рах) при­ве­де­на в таб­ли­це:

 

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми А и E. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, про­тяжённость ко­то­рых ука­за­на в таб­ли­це.

 

1) 6

2) 7

3) 8

4) 9

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из A в E и вы­бе­рем самый ко­рот­кий.

 

Из пунк­та A можно по­пасть в пунк­ты B, C, D.

Из пунк­та B можно по­пасть в пункт C.

Из пунк­та C можно по­пасть в пунк­ты D, E.

 

A—B—C—E: длина марш­ру­та 7 км.

A—С—E: длина марш­ру­та 8 км.

A—D—C—E: длина марш­ру­та 9 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

Ответ: 2

203

2

Источник: ГИА по информатике 31.05.2013. Основная волна. Вариант 1311.

12. За­да­ние 3 № 223. Между населёнными пунк­та­ми А, В, С, D, Е по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых (в ки­ло­мет­рах) при­ве­де­на в таб­ли­це:

 

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми А и E. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, про­тяжённость ко­то­рых ука­за­на в таб­ли­це.

 

1) 6

2) 7

3) 8

4) 9

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из A в E и вы­бе­рем самый ко­рот­кий.

 

Из пунк­та A можно по­пасть в пунк­ты B, D.

Из пунк­та B можно по­пасть в пунк­ты C, D.

Из пунк­та C можно по­пасть в пунк­ты D, E.

 

A—B—C—E: длина марш­ру­та 9 км.

A—D—B—C—E: длина марш­ру­та 12 км.

A—D—C—E: длина марш­ру­та 9 км.

A—B—D—C—E: длина марш­ру­та 8 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 3.

Ответ: 3

223

3

Источник: ГИА по информатике 31.05.2013. Основная волна. Вариант 1312.

13. За­да­ние 3 № 243. Между населёнными пунк­та­ми А, В, С, D, Е по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых (в ки­ло­мет­рах) при­ве­де­на в таб­ли­це:

 

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми А и E. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, про­тяжённость ко­то­рых ука­за­на в таб­ли­це.

 

1) 6

2) 7

3) 8

4) 9

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из A в E и вы­бе­рем самый ко­рот­кий.

 

Из пунк­та A можно по­пасть в пунк­ты B, C.

Из пунк­та B можно по­пасть в пунк­ты D, E.

Из пунк­та C можно по­пасть в пункт D.

Из пунк­та D можно по­пасть в пункт E.

 

A—B—D—E: длина марш­ру­та 9 км.

A—B—E: длина марш­ру­та 9 км.

A—C—D—E: длина марш­ру­та 8 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 3.

Ответ: 3

243

3

Источник: ГИА по информатике 31.05.2013. Основная волна. Вариант 1313.

14. За­да­ние 3 № 263. Между населёнными пунк­та­ми А, В, С, D, Е по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых (в ки­ло­мет­рах) при­ве­де­на в таб­ли­це:

 

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми А и E. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, про­тяжённость ко­то­рых ука­за­на в таб­ли­це.

 

1) 4

2) 5

3) 6

4) 7

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из A в E и вы­бе­рем самый ко­рот­кий.

 

Из пунк­та A можно по­пасть в пунк­ты B, C, D.

Из пунк­та B можно по­пасть в пункт C.

Из пунк­та C можно по­пасть в пунк­ты D, E.

 

A—B—C—E: длина марш­ру­та 5 км.

A—C—E: длина марш­ру­та 7 км.

A—D—C—E: длина марш­ру­та 6 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

Ответ: 2

263

2

Источник: ГИА по информатике 31.05.2013. Основная волна. Вариант 1314.

15. За­да­ние 3 № 283. Между населёнными пунк­та­ми А, В, С, D, Е по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых (в ки­ло­мет­рах) при­ве­де­на в таб­ли­це:

 

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми А и E. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, про­тяжённость ко­то­рых ука­за­на в таб­ли­це.

 

1) 7

2) 8

3) 9

4) 10

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из A в E и вы­бе­рем самый ко­рот­кий.

 

Из пунк­та A можно по­пасть в пунк­ты B, C.

Из пунк­та B можно по­пасть в пунк­ты C, D.

Из пунк­та C можно по­пасть в пункт D.

Из пунк­та D можно по­пасть в пункт E.

 

A—B—C—D—E: длина марш­ру­та 9 км.

A—C—D—E: длина марш­ру­та 8 км.

A—B—D—E: длина марш­ру­та 10 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

Ответ: 2

283

2

Источник: ГИА по информатике 31.05.2013. Основная волна. Вариант 1315.

16. За­да­ние 3 № 303. Между населёнными пунк­та­ми А, В, С, D, Е по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых (в ки­ло­мет­рах) при­ве­де­на в таб­ли­це:

 

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми А и E. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, про­тяжённость ко­то­рых ука­за­на в таб­ли­це.

 

1) 13

2) 12

3) 11

4) 10

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из A в E и вы­бе­рем самый ко­рот­кий.

 

Из пунк­та A можно по­пасть в пунк­ты B, C.

Из пунк­та B можно по­пасть в пунк­ты C, E.

Из пунк­та C можно по­пасть в пункт D.

Из пунк­та D можно по­пасть в пункт E.

 

A—B—C—D—E: длина марш­ру­та 18 км.

A—B—E: длина марш­ру­та 12 км.

A—C—D—E: длина марш­ру­та 13 км.

А—С—В—Е: длина марш­ру­та 11 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 3.

Ответ: 3

303

3

Источник: ГИА по информатике 31.05.2013. Основная волна. Вариант 1316.

17. За­да­ние 3 № 323. Между населёнными пунк­та­ми А, В, С, D, Е по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых (в ки­ло­мет­рах) при­ве­де­на в таб­ли­це:

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми А и F. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, про­тяжённость ко­то­рых ука­за­на в таб­ли­це.

 

1) 9

2) 11

3) 13

4) 15

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из A в E и вы­бе­рем самый ко­рот­кий.

 

Из пунк­та A можно по­пасть в пунк­ты B, C, F.

Из пунк­та B можно по­пасть в пункт C.

Из пунк­та C можно по­пасть в пунк­ты D, E.

Из пунк­та D можно по­пасть в пункт F.

Из пунк­та E можно по­пасть в пункт F.

 

A—F: длина марш­ру­та 15 км.

A—B—C—E—F: длина марш­ру­та 15 км.

A—B—C—D—F: длина марш­ру­та 14 км.

A—C—E—F: длина марш­ру­та 14 км.

A—C—D—F: длина марш­ру­та 13 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 3.

Ответ: 3

323

3

Источник: Демонстрационная вер­сия ГИА—2013 по информатике.

18. За­да­ние 3 № 344. Между населёнными пунк­та­ми А, В, С, D, Е по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых (в ки­ло­мет­рах) при­ве­де­на в таб­ли­це:

 

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми А и F. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, про­тяжённость ко­то­рых ука­за­на в таб­ли­це.

 

1) 5

2) 6

3) 7

4) 4

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из A в E и вы­бе­рем самый ко­рот­кий.

 

Из пунк­та A можно по­пасть в пунк­ты B, C, D, E .

Из пунк­та B можно по­пасть в пункт C.

Из пунк­та C можно по­пасть в пунк­ты D, F.

Из пунк­та D можно по­пасть в пункт E.

Из пунк­та E можно по­пасть в пункт F.

 

A—E—F: длина марш­ру­та 7 км.

A—B—C—F: длина марш­ру­та 8 км.

A—C—D—E—F: длина марш­ру­та 14 км.

A—D—E—F: длина марш­ру­та 9 км.

A—C—F: длина марш­ру­та 5 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 1.

Ответ: 1

344

1

Источник: Типовые эк­за­ме­на­ци­он­ные варианты. Кры­лов С. С., Чур­ки­на Т. Е. — 2013, ва­ри­ант 1.

19. За­да­ние 3 № 364. Между населёнными пунк­та­ми А, В, С, D, Е, F по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых при­ве­де­на в таб­ли­це:

 

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми А и F. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, про­тяжённость ко­то­рых ука­за­на в таб­ли­це.

 

 

1) 5

2) 6

3) 7

4) 4

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из A в F и вы­бе­рем самый ко­рот­кий.

 

A-B-C-D-E-F: длина марш­ру­та 18 км.

A-B-C-F: длина марш­ру­та 9 км.

A-C-D-E-F: длина марш­ру­та 15 км.

A-C-F: длина марш­ру­та 6 км.

A-D-C-F: длина марш­ру­та 7 км.

A-D-E-F: длина марш­ру­та 10 км.

A-E-D-C-F: длина марш­ру­та 8 км.

A-E-F: длина марш­ру­та 7 км.

 

Крат­чай­ший марш­рут имеет длину 6 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

Ответ: 2

364

2

Источник: Типовые эк­за­ме­на­ци­он­ные ва­ри­ан­ты по информатике. Кры­лов С. С., Чур­ки­на Т. Е. — 2013, ва­ри­ант 2.

20. За­да­ние 3 № 384. Между населёнными пунк­та­ми А, В, С, D, Е, F по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых (в ки­ло­мет­рах) при­ве­де­на в таб­ли­це:

 

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми А и F. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, про­тяжённость ко­то­рых ука­за­на в таб­ли­це.

 

1) 5

2) 6

3) 7

4) 8

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из A в E и вы­бе­рем самый ко­рот­кий.

 

Из пунк­та A можно по­пасть в пунк­ты B, C, D.

Из пунк­та B можно по­пасть в пункт C.

Из пунк­та C можно по­пасть в пункт F.

Из пунк­та D можно по­пасть в пунк­ты E, F.

Из пунк­та E можно по­пасть в пункт F.

 

A—C—F: длина марш­ру­та 6 км.

A—B—C—F: длина марш­ру­та 8 км.

A—D—E—F: длина марш­ру­та 6 км.

A—D—F: длина марш­ру­та 7 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

Ответ: 2

384

2

Источник: Типовые эк­за­ме­на­ци­он­ные ва­ри­ан­ты по информатике. Кры­лов С. С., Чур­ки­на Т. Е. — 2013, ва­ри­ант 3.

21. За­да­ние 3 № 404. Между населёнными пунк­та­ми А, В, С, D, Е, F по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых при­ве­де­на в таб­ли­це:

 

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми А и F. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, про­тяжённость ко­то­рых ука­за­на в таб­ли­це.

 

1) 5

2) 6

3) 7

4) 9

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из A в E и вы­бе­рем самый ко­рот­кий.

 

Из пунк­та A можно по­пасть в пунк­ты B, C, D.

Из пунк­та B можно по­пасть в пункт C.

Из пунк­та C можно по­пасть в пункт F.

Из пунк­та D можно по­пасть в пунк­ты E, F.

Из пунк­та E можно по­пасть в пункт F.

 

A—B—C—F: длина марш­ру­та 9 км.

A—C—F: длина марш­ру­та 7 км.

A—D—E—F: длина марш­ру­та 7 км.

A—D—F: длина марш­ру­та 7 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 3.

Ответ: 3

404

3

Источник: Типовые эк­за­ме­на­ци­он­ные ва­ри­ан­ты по информатике. Кры­лов С. С., Чур­ки­на Т. Е. — 2013, ва­ри­ант 4.

22. За­да­ние 3 № 424. Между населёнными пунк­та­ми А, В, С, D, Е, F по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых при­ве­де­на в таб­ли­це:

 

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми А и F. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, про­тяжённость ко­то­рых ука­за­на в таб­ли­це.

 

1) 6

2) 7

3) 8

4) 9

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из A в F и вы­бе­рем самый ко­рот­кий.

 

Из пунк­та A можно по­пасть в пунк­ты B, C, F.

Из пунк­та B можно по­пасть в пунк­ты C, D, F.

Из пунк­та C можно по­пасть в пункт E.

Из пунк­та E можно по­пасть в пункт F.

 

A—C—E—F: длина марш­ру­та 7 км.

A—F: длина марш­ру­та 9 км.

A—B—C—E—F: длина марш­ру­та 6 км.

A—B—F: длина марш­ру­та 7 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 1.

Ответ: 1

424

1

Источник: Типовые эк­за­ме­на­ци­он­ные ва­ри­ан­ты по информатике. Кры­лов С. С., Чур­ки­на Т. Е. — 2013, ва­ри­ант 5.

23. За­да­ние 3 № 444. Между населёнными пунк­та­ми А, В, С, D, Е, F по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых при­ве­де­на в таб­ли­це:

 

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми А и F. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, про­тяжённость ко­то­рых ука­за­на в таб­ли­це.

 

1) 6

2) 7

3) 8

4) 9

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из A в E и вы­бе­рем самый ко­рот­кий.

 

Из пунк­та A можно по­пасть в пунк­ты B, C, F.

Из пунк­та B можно по­пасть в пунк­ты C, D, F.

Из пунк­та C можно по­пасть в пункт E.

Из пунк­та E можно по­пасть в пункт F.

 

A—C—E—F: длина марш­ру­та 8 км.

A—F: длина марш­ру­та 7 км.

A—B—C—E—F: длина марш­ру­та 7 км.

A—B—F: длина марш­ру­та 7 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

Ответ: 2

444

2

Источник: Типовые эк­за­ме­на­ци­он­ные ва­ри­ан­ты по информатике. Кры­лов С. С., Чур­ки­на Т. Е. — 2013, ва­ри­ант 6.

24. За­да­ние 3 № 464. Между населёнными пунк­та­ми А, В, С, D, Е, F по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых при­ве­де­на в таб­ли­це:

 

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми А и F (при усло­вии, что пе­ре­дви­гать­ся можно толь­ко по по­стро­ен­ным до­ро­гам).

 

1) 5

2) 6

3) 3

4) 4

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из A в F и вы­бе­рем самый ко­рот­кий.

 

Из пунк­та A можно по­пасть в пунк­ты B, C, D, E, F.

Из пунк­та B можно по­пасть в пункт C.

Из пунк­та C можно по­пасть в пункт D.

Из пунк­та D можно по­пасть в пункт E.

Из пунк­та E можно по­пасть в пункт F.

 

A—B—C—D—E—F: длина марш­ру­та 12 км.

A—C—D—E—F: длина марш­ру­та 5 км.

A—D—E—F: длина марш­ру­та 4 км.

A—E—F: длина марш­ру­та 6 км.

A—F: длина марш­ру­та 5 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 4.

Ответ: 4

464

4

Источник: Типовые эк­за­ме­на­ци­он­ные ва­ри­ан­ты по информатике. Кры­лов С. С., Чур­ки­на Т. Е. — 2013, ва­ри­ант 7.

25. За­да­ние 3 № 484. Между населёнными пунк­та­ми А, В, С, D, Е, F по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых при­ве­де­на в таб­ли­це:

 

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми А и F (при усло­вии, что пе­ре­дви­гать­ся можно толь­ко по по­стро­ен­ным до­ро­гам).

 

1) 5

2) 6

3) 7

4) 4

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из A в E и вы­бе­рем самый ко­рот­кий.

 

Из пунк­та A можно по­пасть в пунк­ты B, C, D, E, F.

Из пунк­та B можно по­пасть в пункт C.

Из пунк­та C можно по­пасть в пункт D.

Из пунк­та D можно по­пасть в пункт E.

Из пунк­та E можно по­пасть в пункт F.

 

A—B—C—D—E—F: длина марш­ру­та 14 км.

A—C—D—E—F: длина марш­ру­та 7 км.

A—D—E—F: длина марш­ру­та 6 км.

A—E—F: длина марш­ру­та 7 км.

A—F: длина марш­ру­та 5 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 1.

Ответ: 1

484

1

Источник: Типовые эк­за­ме­на­ци­он­ные ва­ри­ан­ты по информатике. Кры­лов С. С., Чур­ки­на Т. Е. — 2013, ва­ри­ант 8.

26. За­да­ние 3 № 504. Между населёнными пунк­та­ми А, В, С, D, Е, F по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых при­ве­де­на в таб­ли­це:

 

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми А и F (при усло­вии, что пе­ре­дви­гать­ся можно толь­ко по по­стро­ен­ным до­ро­гам).

 

1) 5

2) 7

3) 3

4) 9

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из A в E и вы­бе­рем самый ко­рот­кий.

 

Из пунк­та A можно по­пасть в пунк­ты C, D.

Из пунк­та B можно по­пасть в пунк­ты C, F.

Из пунк­та C можно по­пасть в пункт F.

Из пунк­та D можно по­пасть в пунк­ты E, F.

Из пунк­та E можно по­пасть в пункт F.

 

A—C—F: длина марш­ру­та 6 км.

A—C—B—F: длина марш­ру­та 6 км.

A—D—E—F: длина марш­ру­та 7 км.

A—D—F: длина марш­ру­та 5 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 1.

Ответ: 1

504

1

Источник: Типовые эк­за­ме­на­ци­он­ные ва­ри­ан­ты по информатике. Кры­лов С. С., Чур­ки­на Т. Е. — 2013, ва­ри­ант 9.

27. За­да­ние 3 № 524. Между населёнными пунк­та­ми А, В, С, D, Е, F по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых при­ве­де­на в таб­ли­це:

 

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми А и F (при усло­вии, что пе­ре­дви­гать­ся можно толь­ко по по­стро­ен­ным до­ро­гам).

 

1) 6

2) 8

3) 10

4) 4

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из A в E и вы­бе­рем самый ко­рот­кий.

 

Из пунк­та A можно по­пасть в пунк­ты C, D.

Из пунк­та B можно по­пасть в пунк­ты C, F.

Из пунк­та C можно по­пасть в пункт F.

Из пунк­та D можно по­пасть в пунк­ты E, F.

Из пунк­та E можно по­пасть в пункт F.

 

A—C—F: длина марш­ру­та 8 км.

A—C—B—F: длина марш­ру­та 6 км.

A—D—E—F: длина марш­ру­та 7 км.

A—D—F: длина марш­ру­та 7 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 1.

Ответ: 1

524

1

Источник: Типовые эк­за­ме­на­ци­он­ные ва­ри­ан­ты по информатике. Кры­лов С. С., Чур­ки­на Т. Е. — 2013, ва­ри­ант 10.

28. За­да­ние 3 № 544. Иван-Ца­ре­вич спе­шит вы­ру­чить Марью-Ца­рев­ну из плена Кощея. В таб­ли­це ука­за­на про­тяжённость дорог между пунк­та­ми, через ко­то­рые он может прой­ти. Ука­жи­те длину са­мо­го длин­но­го участ­ка крат­чай­ше­го пути от Ивана-Ца­ре­ви­ча до Марьи Ца­рев­ны (от точки И до точки М). Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, ука­зан­ным в таб­ли­це:

 

 

1) 1

2) 2

3) 3

4) 6

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из И в М и вы­бе­рем самый ко­рот­кий.

 

Из пунк­та И можно по­пасть в пунк­ты А, Б, Г, М.

Из пунк­та Г можно по­пасть в пунк­ты И, М.

Из пунк­та В можно по­пасть в пунк­ты А, Б.

Из пунк­та Б можно по­пасть в пунк­ты В, И, М.

 

И—А—В—Б—М: длина марш­ру­та 7 км.

И—Б—М: длина марш­ру­та 4 км.

И—Г—М: длина марш­ру­та 7 км.

И—М: длина марш­ру­та 8 км.

 

Самый ко­рот­кий путь: И—Б—М; Длина марш­ру­та 4 км, самый длин­ный уча­сток этого пути равен 3.

Ответ: 3

544

3

Источник: МИОО: Тре­ни­ро­воч­ная работа по ин­фор­ма­ти­ке 07.05.2013 ва­ри­ант ИН9601.

29. За­да­ние 3 № 564. Иван-Ца­ре­вич спе­шит вы­ру­чить Марью-Ца­рев­ну из плена Кощея. В таб­ли­це ука­за­на про­тяжённость дорог между пунк­та­ми, через ко­то­рые он может прой­ти. Ука­жи­те длину са­мо­го ко­рот­ко­го участ­ка крат­чай­ше­го пути от Ивана-Ца­ре­ви­ча до Марьи Ца­рев­ны (от точки И до точки М). Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, ука­зан­ным в таб­ли­це:

 

 

1) 1

2) 2

3) 3

4) 4

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из И в М и вы­бе­рем самый ко­рот­кий.

 

Из пунк­та И можно по­пасть в пунк­ты А, Б, Г, М.

Из пунк­та Г можно по­пасть в пунк­ты И, М.

Из пунк­та В можно по­пасть в пунк­ты А, Б.

Из пунк­та Б можно по­пасть в пунк­ты В, И, М.

 

И—А—В—Б—М: длина марш­ру­та 7 км.

И—Б—М: длина марш­ру­та 4 км.

И—Г—М: длина марш­ру­та 7 км.

И—М: длина марш­ру­та 8 км.

 

Самый ко­рот­кий путь: И—Б—М; Длина марш­ру­та 4 км, самый ко­рот­кий уча­сток этого пути равен 1.

Ответ: 1

564

1

Источник: МИОО: Тре­ни­ро­воч­ная работа по ин­фор­ма­ти­ке 07.05.2013 ва­ри­ант ИН9602.

30. За­да­ние 3 № 584. У Пети Ива­но­ва род­ствен­ни­ки живут в 5 раз­ных го­ро­дах Рос­сии. Рас­сто­я­ния между го­ро­да­ми вне­се­ны в таб­ли­цу:

 

 

Петя пе­ре­ри­со­вал её в блок­нот в виде графа. Счи­тая, что маль­чик не ошиб­ся при ко­пи­ро­ва­нии, ука­жи­те, какой граф у Пети в тет­ра­ди.

 

1)

2)

3)

4)

По­яс­не­ние.

Про­ве­рим по­сле­до­ва­тель­но каж­дый граф.

 

1) Не со­от­вет­ству­ет таб­ли­це, по­сколь­ку со­глас­но графу не су­ще­ству­ет пря­мой до­ро­ги из пунк­та A в пункт D.

2) Не со­от­вет­ству­ет таб­ли­це, по­сколь­ку со­глас­но графу рас­сто­я­ние между пунк­та­ми D и B равно 3.

3) Граф со­от­вет­ству­ет таб­ли­це.

4) Не со­от­вет­ству­ет таб­ли­це, по­сколь­ку со­глас­но графу не су­ще­ству­ет пря­мой до­ро­ги из пунк­та D в пункт C.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 3.

Ответ: 3

584

3

Источник: МИОО: Тре­ни­ро­воч­ная работа по ин­фор­ма­ти­ке 10.04.2013 ва­ри­ант ИН9501.

31. За­да­ние 3 № 604. У Кати Ев­ту­шен­ко род­ствен­ни­ки живут в 5 раз­ных го­ро­дах Рос­сии. Рас­сто­я­ния между го­ро­да­ми вне­се­ны в таб­ли­цу:

 

 

Катя пе­ре­ри­со­вала её в блок­нот в виде графа. Счи­тая, что де­воч­ка не ошиб­лась при ко­пи­ро­ва­нии, ука­жи­те, какой граф у Кати в тет­ра­ди.

 

1)

2)

3)

4)

По­яс­не­ние.

Про­ве­рим по­сле­до­ва­тель­но каж­дый граф.

 

1) Не со­от­вет­ству­ет таб­ли­це, по­сколь­ку со­глас­но графу не су­ще­ству­ет пря­мой до­ро­ги из пунк­та C в пункт E.

2) Граф со­от­вет­ству­ет таб­ли­це.

3) Не со­от­вет­ству­ет таб­ли­це, по­сколь­ку со­глас­но графу не су­ще­ству­ет пря­мой до­ро­ги из пунк­та D в пункт B.

4) Не со­от­вет­ству­ет таб­ли­це, по­сколь­ку со­глас­но графу не су­ще­ству­ет пря­мой до­ро­ги из пунк­та B в пункт E.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

Ответ: 2

604

2

Источник: МИОО: Тре­ни­ро­воч­ная работа по ин­фор­ма­ти­ке 10.04.2013 ва­ри­ант ИН9502.

32. За­да­ние 3 № 624. Учи­тель Иван Пет­ро­вич живёт на стан­ции Ан­то­нов­ка, а ра­бо­та­ет на стан­ции Друж­ба. Чтобы успеть с утра на уроки, он дол­жен ехать по самой ко­рот­кой до­ро­ге. Про­ана­ли­зи­руй­те таб­ли­цу и ука­жи­те длину крат­чай­ше­го пути от стан­ции Ан­то­нов­ка до стан­ции Друж­ба:

 

 

1) 6

2) 2

3) 8

4) 4

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из Ан­то­нов­ки в Друж­бу и вы­бе­рем самый ко­рот­кий.

 

Из пунк­та Ан­то­нов­ка(А) можно по­пасть в пунк­ты Ва­силь­ки(В), Еже­вич­ная(Е).

Из пунк­та B можно по­пасть в пункт Друж­ба(Д).

Из пунк­та Сель­ская(С) можно по­пасть в пунк­ты Д, Е.

Из пунк­та Д можно по­пасть в пункт Е.

 

А—В—Д: длина марш­ру­та 6 км.

А—Е—Д: длина марш­ру­та 8 км.

А—Е—С—Д: длина марш­ру­та 4 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 4.

Ответ: 4

624

4

Источник: МИОО: Тре­ни­ро­воч­ная работа по ин­фор­ма­ти­ке 31.01.2013 ва­ри­ант 1.

33. За­да­ние 3 № 644. Учи­тель­ни­ца Марья Пет­ров­на живёт на стан­ции Ва­силь­ки, а ра­бо­та­ет на стан­ции Друж­ба. Чтобы успеть с утра на уроки, она долж­на ехать по самой ко­рот­кой до­ро­ге. Про­ана­ли­зи­руй­те таб­ли­цу и ука­жи­те длину крат­чай­ше­го пути от стан­ции Ва­силь­ки до стан­ции Друж­ба:

 

 

1) 5

2) 6

3) 8

4) 9

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов от стан­ции Ва­силь­ки до стан­ции Друж­ба и вы­бе­рем самый ко­рот­кий.

 

Из пунк­та Ан­то­нов­ка(А) можно по­пасть в пунк­ты Ва­силь­ки(В), Еже­вич­ная(Е).

Из пунк­та B можно по­пасть в пункт Сель­ская(С).

Из пунк­та С можно по­пасть в пунк­ты Д, Е.

Из пунк­та Д можно по­пасть в пункт Е.

 

В—А—Е—Д: длина марш­ру­та 9 км.

В—А—Е—С—Д: длина марш­ру­та 6 км.

В—С—Д: длина марш­ру­та 8 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

Ответ: 2

644

2

Источник: МИОО: Тре­ни­ро­воч­ная работа по ин­фор­ма­ти­ке 31.01.2013 ва­ри­ант 2.

34. За­да­ние 3 № 664. Сель­ская ма­ло­ком­плект­ная школа на­хо­дит­ся в по­сел­ке Ива­нов­ское. Коля Ива­нов живёт в де­рев­не Верш­ки. Опре­де­ли­те, какое ми­ни­маль­ное рас­сто­я­ние ему надо прой­ти, чтобы до­брать­ся до школы:

 

 

1) 6

2) 9

3) 12

4) 14

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов от де­рев­ни Верш­ки до по­сел­ка Ива­нов­ское и вы­бе­рем самый ко­рот­кий.

 

Из пунк­та Верш­ки(В) можно по­пасть в пунк­ты Борки(Б), Даль­нее(Да) и Ду­бо­во(Ду).

Из пунк­та Б можно по­пасть в пунк­ты Крас­ное(К), Да, Ива­нов­ское(И).

Из пунк­та К можно по­пасть в пунк­ты Ду, И.

Из пунк­та Да можно по­пасть в пункт И.

 

В—Б—К—И: длина марш­ру­та 16 км.

В—Б—Да—И: длина марш­ру­та 20 км.

В—Б—И: длина марш­ру­та 14 км.

В—Да—И: длина марш­ру­та 9 км.

В—Ду—К—И: длина марш­ру­та 6 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 1.

Ответ: 1

664

1

Источник: МИОО: Ди­а­гно­сти­че­ская работа по ин­фор­ма­ти­ке 15.03.2013 ва­ри­ант ИНФ9403.

35. За­да­ние 3 № 684. Сель­ская ма­ло­ком­плект­ная школа на­хо­дит­ся в по­сел­ке Верш­ки. Петя Орлов живёт в де­рев­не Даль­нее. Опре­де­ли­те, какое ми­ни­маль­ное рас­сто­я­ние ему надо прой­ти, чтобы до­брать­ся до школы:

 

 

1) 6

2) 8

3) 11

4) 15

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов от де­рев­ни Даль­нее до по­сел­ка Верш­ки и вы­бе­рем самый ко­рот­кий.

 

Из пунк­та Даль­нее(Да) можно по­пасть в пунк­ты Борки(Б), Крас­ное(К), Ду­бо­во(Ду) и Ива­нов­ское(И).

Из пунк­та Крас­ное(К) можно по­пасть в пунк­ты Б, Ду, И .

Из пунк­та Верш­ки(В) можно по­пасть в пунк­ты Б, Ду.

Из пунк­та Б можно по­пасть в пункт И.

 

Да—Б—В: длина марш­ру­та 15 км.

Да—Б—К—Ду—В: длина марш­ру­та 21 км.

Да—К—Ду—В: длина марш­ру­та 8 км.

Да—Ду—В: длина марш­ру­та 9 км.

Да—И—Б—В: длина марш­ру­та 19 км.

Да—И—Б—К—Ду—В: длина марш­ру­та 17 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

Ответ: 2

684

2

Источник: МИОО: Ди­а­гно­сти­че­ская работа по ин­фор­ма­ти­ке 15.03.2013 ва­ри­ант ИНФ9404.

36. За­да­ние 3 № 704. Между населёнными пунк­та­ми A, B, C, D, E по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых(в ки­ло­мет­рах) при­ве­дена в таб­ли­це.

 

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми А и E. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, про­тяжённость ко­то­рых ука­за­на в таб­ли­це.

 

1) 4

2) 5

3) 6

4) 7

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из A в E и вы­бе­рем самый ко­рот­кий.

 

Из пунк­та A можно по­пасть в пунк­ты B, C, D.

Из пунк­та B можно по­пасть в пункт C.

Из пунк­та C можно по­пасть в пунк­ты D, E.

 

A—B—C—E: длина марш­ру­та 5 км.

A—С—E: длина марш­ру­та 7 км.

A—D—C—E: длина марш­ру­та 6 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

Ответ: 2

704

2

Источник: Демонстрационная вер­сия ГИА—2014 по информатике.

37. За­да­ние 3 № 747. Во­ди­тель ав­то­мо­би­ля дол­жен до­брать­ся из пунк­та А в пункт D за 5 часов. Из пред­став­лен­ных таб­лиц вы­бе­ри­те такую, со­глас­но ко­то­рой во­ди­тель смо­жет до­е­хать из пунк­та А в пункт D за это время. В ячей­ках таб­ли­цы ука­за­но время (в часах), ко­то­рое за­ни­ма­ет до­ро­га из од­но­го пунк­та в дру­гой. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, ука­зан­ным в таб­ли­цах.

 

 

 

1) 1

2) 2

3) 3

4) 4

По­яс­не­ние.

Найдём крат­чай­шие марш­ру­ты из A в D для каж­дой таб­ли­цы.

 

Ис­хо­дя из пер­вой таб­ли­цы, крат­чай­ший марш­рут из A в D: A—C—B—D, его можно пре­одо­леть за 6 часов. Крат­чай­ший марш­рут из A в D для вто­рой таб­ли­цы: A—B—D, его можно пре­одо­леть за 5 часов. Для тре­тьей таб­ли­цы крат­чай­шая до­ро­га: A—C—B—D, она за­ни­ма­ет 6 часов. Для четвёртой таб­ли­цы крат­чай­ший марш­рут: A—D, его можно пре­одо­леть за 6 часов.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

Ответ: 2

747

2

Источник: МИОО: Тре­ни­ро­воч­ная работа по ин­фор­ма­ти­ке 18.10.2013 ва­ри­ант ИНФ9101.

38. За­да­ние 3 № 767. Во­ди­тель ав­то­мо­би­ля дол­жен до­брать­ся из пунк­та А в пункт C за 6 часов. Из пред­став­лен­ных таб­лиц вы­бе­ри­те такую, со­глас­но ко­то­рой во­ди­тель смо­жет до­е­хать из пунк­та А в пункт C за это время. В ячей­ках таб­ли­цы ука­за­но время (в часах), ко­то­рое за­ни­ма­ет до­ро­га из од­но­го пунк­та в дру­гой. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, ука­зан­ным в таб­ли­цах.

 

 

 

1) 1

2) 2

3) 3

4) 4

По­яс­не­ние.

Найдём крат­чай­шие марш­ру­ты из A в С для каж­дой таб­ли­цы.

 

Ис­хо­дя из пер­вой таб­ли­цы, крат­чай­ший марш­рут из A в С: A—C, его можно пре­одо­леть за 7 часов. Крат­чай­ший марш­рут из A в С для вто­рой таб­ли­цы: A—B—С, за­ни­ма­ет 7 часов. Для тре­тьей таб­ли­цы крат­чай­шая до­ро­га: A—B—C, она за­ни­ма­ет 7 часов. Для четвёртой таб­ли­цы крат­чай­ший марш­рут: A—B—C, его можно пре­одо­леть за 6 часов.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 4.

Ответ: 4

767

4

Источник: МИОО: Тре­ни­ро­воч­ная работа по ин­фор­ма­ти­ке 18.10.2013 ва­ри­ант ИНФ9102.

39. За­да­ние 3 № 799. Между населёнными пунк­та­ми A, B, C, D, E по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых (в ки­ло­мет­рах) при­ве­де­на в таб­ли­це.

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми A и B. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, про­тяжённость ко­то­рых ука­за­на в таб­ли­це.

 

1) 4

2) 6

3) 10

4) 12

По­яс­не­ние.

Ис­кать сле­ду­ет марш­рут, длина ко­то­ро­го не пре­вы­ша­ет 12 км, по­сколь­ку длина A—B со­став­ля­ет 12 км. Рас­смот­рим марш­ру­ты:

 

A—C—B: длина марш­ру­та 10 км,

A—D—B: длина марш­ру­та 6 км,

A—E—B: длина марш­ру­та 6 км,

A—C—D—B: длина марш­ру­та 4 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 1.

Ответ: 1

799

1

Источник: МИОО: Ди­а­гно­сти­че­ская работа по ин­фор­ма­ти­ке 06.03.2014 ва­ри­ант ИН90701.

40. За­да­ние 3 № 819. Между населёнными пунк­та­ми A, B, C, D, E по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых (в ки­ло­мет­рах) при­ве­де­на в таб­ли­це.

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми A и B. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, про­тяжённость ко­то­рых ука­за­на в таб­ли­це.

 

1) 1

2) 5

3) 3

4) 7

По­яс­не­ние.

Ис­кать сле­ду­ет марш­рут, длина ко­то­ро­го не пре­вы­ша­ет 5 км, по­сколь­ку длина A—B со­став­ля­ет 5 км. Рас­смот­рим марш­ру­ты:

 

A—C—E—B: длина марш­ру­та 3 км,

A—D—B: длина марш­ру­та 7 км,

A—D—E—B: длина марш­ру­та 5 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 3.

Ответ: 3

819

3

Источник: МИОО: Ди­а­гно­сти­че­ская работа по ин­фор­ма­ти­ке 06.03.2014 ва­ри­ант ИН90702.

41. За­да­ние 3 № 841. Между населёнными пунк­та­ми A, B, C, D, E по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых (в ки­ло­мет­рах) при­ве­де­на в таб­ли­це.

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми A и B (при усло­вии, что пе­ре­дви­гать­ся можно толь­ко по по­стро­ен­ным до­ро­гам).

 

1) 11

2) 12

3) 13

4) 14

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из A в B и вы­бе­рем самый ко­рот­кий.

 

A—C—D—B: длина марш­ру­та 13 км.

A—C—E—B: длина марш­ру­та 12 км.

A—D—C—E—B: длина марш­ру­та 15 км.

A—D—B: длина марш­ру­та 14 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

Ответ: 2

841

2

Источник: МИОО: Ди­а­гно­сти­че­ская ра­бо­та по ин­фор­ма­ти­ке 19.12.2013 ва­ри­ант ИНФ90301.

42. За­да­ние 3 № 861. Между населёнными пунк­та­ми A, B, C, D, E по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых (в ки­ло­мет­рах) при­ве­де­на в таб­ли­це.

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми A и C (при усло­вии, что пе­ре­дви­гать­ся можно толь­ко по по­стро­ен­ным до­ро­гам).

 

1) 6

2) 7

3) 8

4) 9

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из A в C и вы­бе­рем самый ко­рот­кий.

 

A—B—D—E—C: длина марш­ру­та 14 км.

A—B—D—C: длина марш­ру­та 7 км.

A—B—E—C: длина марш­ру­та 6 км.

A—D—C: длина марш­ру­та 9 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 1.

Ответ: 1

861

1

Источник: МИОО: Ди­а­гно­сти­че­ская ра­бо­та по ин­фор­ма­ти­ке 19.12.2013 ва­ри­ант ИНФ90302.

43. За­да­ние 3 № 882. Между населёнными пунк­та­ми A, B, C, D, E по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых (в ки­ло­мет­рах) при­ве­де­на в таб­ли­це.

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми A и D. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, про­тяжённость ко­то­рых ука­за­на в таб­ли­це.

 

1) 5

2) 6

3) 7

4) 8

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из A в D и вы­бе­рем самый ко­рот­кий.

 

A—B—C—D: длина марш­ру­та 9 км.

A—C—E—B: длина марш­ру­та 12 км.

A—D: длина марш­ру­та 8 км.

A—E—D: длина марш­ру­та 6 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

Ответ: 2

882

2

Источник: МИОО: Тре­ни­ро­воч­ная ра­бо­та по ин­фор­ма­ти­ке 17.02.2014 ва­ри­ант ИН90501.

44. За­да­ние 3 № 902. Между населёнными пунк­та­ми A, B, C, D, E по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых (в ки­ло­мет­рах) при­ве­де­на в таб­ли­це.

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми A и E. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, про­тяжённость ко­то­рых ука­за­на в таб­ли­це.

 

1) 4

2) 6

3) 8

4) 10

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из A в D и вы­бе­рем самый ко­рот­кий.

 

A—B—C—E: длина марш­ру­та 6 км.

A—B—D—E: длина марш­ру­та 12 км.

A—D—E: длина марш­ру­та 16 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

Ответ: 2

902

2

Источник: МИОО: Тре­ни­ро­воч­ная ра­бо­та по ин­фор­ма­ти­ке 17.02.2014 ва­ри­ант ИН90502.

45. За­да­ние 3 № 922. Между населёнными пунк­та­ми A, B, C, D, E по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых (в ки­ло­мет­рах) при­ве­де­на в таб­ли­це.

 

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми A и C. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, про­тяжённость ко­то­рых ука­за­на в таб­ли­це.

 

1) 3

2) 5

3) 8

4) 9

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из A в С и вы­бе­рем самый ко­рот­кий.

 

A—B—C: длина марш­ру­та 9 км.

A—C: длина марш­ру­та 8 км.

A—D—C: длина марш­ру­та 12 км.

A—D—E—C: длина марш­ру­та 5 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

Ответ: 2

922

2

Источник: МИОО: Тре­ни­ро­воч­ная ра­бо­та по ин­фор­ма­ти­ке 24.04.2014 ва­ри­ант ИН90801.

46. За­да­ние 3 № 942. Между населёнными пунк­та­ми A, B, C, D, E по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых (в км) при­ве­де­на в таб­ли­це.

 

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми A и C. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, про­тяжённость ко­то­рых ука­за­на в таб­ли­це.

 

1) 7

2) 8

3) 9

4) 12

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из A в С и вы­бе­рем самый ко­рот­кий.

 

A—B—C: длина марш­ру­та 9 км.

A—C: длина марш­ру­та 9 км.

A—D—C: длина марш­ру­та 8 км.

A—D—E—C: длина марш­ру­та 7 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 1.

Ответ: 1

942

1

Источник: МИОО: Тре­ни­ро­воч­ная ра­бо­та по ин­фор­ма­ти­ке 24.04.2014 ва­ри­ант ИН90802.

47. За­да­ние 3 № 1014. Ма­ши­нист элек­тро­по­ез­да дол­жен до­брать­ся из пунк­та А в пункт C за 6 часов. Из пред­став­лен­ных таб­лиц вы­бе­ри­те такую, со­глас­но ко­то­рой ма­ши­нист смо­жет до­е­хать из пунк­та А в пункт C за это время. В ячей­ках таб­ли­цы ука­за­но время (в часах), ко­то­рое за­ни­ма­ет до­ро­га из од­но­го пунк­та в дру­гой. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, ука­зан­ным в таб­ли­цах.

По­яс­не­ние.

Найдём крат­чай­шие марш­ру­ты из A в С для каж­дой таб­ли­цы.

 

Ис­хо­дя из пер­вой таб­ли­цы, крат­чай­ший марш­рут из A в С: A—B—C, его можно пре­одо­леть за 8 часов. Для вто­рой таб­ли­цы крат­чай­шая до­ро­га: A—B—C, она за­ни­ма­ет 6 часов.й­ший марш­рут: A—B—C, его можно пре­одо­леть за 7 часов.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

Ответ: 2

1014

2

Источник: СтатГрад: Тренировочная ра­бо­та по ин­фор­ма­ти­ке 20.11.14 ва­ри­ант ИН90101.

48. За­да­ние 3 № 1034. Ма­ши­нист элек­тро­по­ез­да дол­жен до­брать­ся из пунк­та А в пункт C за 4 часа. Из пред­став­лен­ных таб­лиц вы­бе­ри­те такую, со­глас­но ко­то­рой ма­ши­нист смо­жет до­е­хать из пунк­та А в пункт C за это время. В ячей­ках таб­ли­цы ука­за­но время (в часах), ко­то­рое за­ни­ма­ет до­ро­га из од­но­го пунк­та в дру­гой. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, ука­зан­ным в таб­ли­цах.

По­яс­не­ние.

Найдём крат­чай­шие марш­ру­ты из A в С для каж­дой таб­ли­цы.

 

Ис­хо­дя из пер­вой таб­ли­цы, крат­чай­ший марш­рут из A в С: A—B—C, его можно пре­одо­леть за 7 часов. Крат­чай­ший марш­рут из A в С для вто­рой таб­ли­цы: A—D—С, за­ни­ма­ет 8 часов. Для тре­тьей таб­ли­цы крат­чай­шая до­ро­га: A—D—С, она за­ни­ма­ет 7 часов. Для четвёртой таб­ли­цы крат­чай­ший марш­рут: A—B—D—С, его можно пре­одо­леть за 4 часа.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 4.

Ответ: 4

1034

4

Источник: СтатГрад: Тре­ни­ро­воч­ная ра­бо­та по ин­фор­ма­ти­ке 20.11.14 ва­ри­ант ИН90102.

49. За­да­ние 3 № 1054. В таб­ли­це при­ве­де­на сто­и­мость пе­ре­во­зок между пятью же­лез­но­до­рож­ны­ми стан­ци­я­ми, обо­зна­чен­ны­ми бук­ва­ми A, B, C, D и E. Ука­жи­те схему, со­от­вет­ству­ю­щую таб­ли­це.

По­яс­не­ние.

Из таб­ли­цы видно, что из пунк­та A есть до­ро­ги в любой дру­гой пункт. Сле­до­ва­тель­но, под­хо­дит толь­ко ва­ри­ант 2.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

Ответ: 2

1054

2

Источник: СтатГрад: Тре­ни­ро­воч­ная ра­бо­та по ин­фор­ма­ти­ке 30.01.15 ва­ри­ант ИН90201.

50. За­да­ние 3 № 1074. В таб­ли­це при­ве­де­на сто­и­мость пе­ре­во­зок между пятью же­лез­но­до­рож­ны­ми стан­ци­я­ми, обо­зна­чен­ны­ми бук­ва­ми A, B, C, D и E. Ука­жи­те схему, со­от­вет­ству­ю­щую таб­ли­це.

По­яс­не­ние.

Из таб­ли­цы видно, что из пунк­та A есть до­ро­ги толь­ко в пунк­ты B и C. Сле­до­ва­тель­но, под­хо­дят толь­ко ва­ри­анты 3 и 4. Рас­сто­я­ние между пунк­та­ми A и C — 1, таким об­ра­зом, под­хо­дит толь­ко ва­ри­ант 4.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 4.

Ответ: 4

1074

4

Источник: СтатГрад: Тре­ни­ро­воч­ная ра­бо­та по ин­фор­ма­ти­ке 30.01.15 ва­ри­ант ИН90202.

51. За­да­ние 3 № 1097. Между населёнными пунк­та­ми A, B, C, D, E по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых (в ки­ло­мет­рах) при­ве­де­на в таб­ли­це.

	A	B	C	D	E
A		1	5		2
B	1			6
C	5			1	7
D		6	1
E	2		7

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми A и D (при усло­вии, что пе­ре­дви­гать­ся можно толь­ко по по­стро­ен­ным до­ро­гам).

 

1) 5

2) 6

3) 7

4) 8

По­яс­не­ние.

Из пунк­та A можно до­брать­ся в пунк­ты B, C и D. Про­ана­ли­зи­ру­ем не­ко­то­рые воз­мож­ные марш­ру­ты.

 

Марш­рут A — B — D, длина 7 км.

Марш­рут A — С — D, длина 6 км.

Марш­рут A — E — С — D явно длин­нее марш­ру­та A — С — D.

 

Любые дру­гие марш­ру­ты будут длин­нее марш­ру­та A — С — D. Таким об­ра­зом, крат­чай­шее рас­сто­я­ние между пунк­та­ми A и D со­став­ля­ет 6 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

Ответ: 2

1097

2

Источник: СтатГрад: Тренировочная работа по ин­фор­ма­ти­ке 23.03.15 ва­ри­ант ИН90601.

52. За­да­ние 3 № 1117. Между населёнными пунк­та­ми A, B, C, D, E по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых (в ки­ло­мет­рах) при­ве­де­на в таб­ли­це.

	A	B	C	D	E
A		2	1		5
B	2		4
C	1	4		1	4
D			1		2
E	5		4	2

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми B и E (при усло­вии, что пе­ре­дви­гать­ся можно толь­ко по по­стро­ен­ным до­ро­гам).

 

1) 5

2) 6

3) 7

4) 8

По­яс­не­ние.

Из пунк­та B можно до­брать­ся в пунк­т C. Про­ана­ли­зи­ру­ем не­ко­то­рые воз­мож­ные марш­ру­ты.

 

Марш­рут B — C — E, длина 8 км.

Марш­рут B — С — A — E, длина 10 км.

Марш­рут B — A — С — D — E, длина 6 км.

 

Любые дру­гие марш­ру­ты будут длин­нее марш­ру­та B — A — С — D — E. Таким об­ра­зом, крат­чай­шее рас­сто­я­ние между пунк­та­ми B и E со­став­ля­ет 6 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

Ответ: 2

1117

2

Источник: СтатГрад: Тре­ни­ро­воч­ная работа по ин­фор­ма­ти­ке 23.03.15 ва­ри­ант ИН90602.

53. За­да­ние 3 № 1137. Между населёнными пунк­та­ми A, B, C, D, E по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых (в ки­ло­мет­рах) при­ве­де­на в таб­ли­це.

	A	B	C	D	E
A		5	6	10	5
B	5			4
C	6			2	7
D	10	4	2		5
E	5		7	5

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми A и D. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, про­тяжённость ко­то­рых ука­за­на в таб­ли­це.

 

1) 14

2) 10

3) 9

4) 8

По­яс­не­ние.

Из пунк­та A можно до­брать­ся в пунк­ты B, C и D. Про­ана­ли­зи­ру­ем не­ко­то­рые воз­мож­ные марш­ру­ты.

 

Марш­рут A — B — D, длина 9 км.

Марш­рут A — С — D, длина 8 км.

Марш­рут A — D, длина 10 км.

 

Любые дру­гие марш­ру­ты будут длин­нее марш­ру­та A — С — D. Таким об­ра­зом, крат­чай­шее рас­сто­я­ние между пунк­та­ми A и D со­став­ля­ет 8 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 4.

Ответ: 4

1137

4

Источник: СтатГрад: Репетиционная работа по ин­фор­ма­ти­ке 24.02.15 ва­ри­ант ИН90501.

54. За­да­ние 3 № 1157. Между населёнными пунк­та­ми A, B, C, D по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых (в ки­ло­мет­рах) при­ве­де­на в таб­ли­це.

	A	B	C	D
A		2	7	4
B	2		5	1
C	7	5		2
D	4	1	2

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми A и C. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, про­тяжённость ко­то­рых ука­за­на в таб­ли­це.

 

1) 4

2) 5

3) 6

4) 7

По­яс­не­ние.

Из пунк­та A можно до­брать­ся в пунк­ты B, C и D. Про­ана­ли­зи­ру­ем не­ко­то­рые воз­мож­ные марш­ру­ты.

 

Марш­рут A — B — C, длина 7 км.

Марш­рут A — D — C, длина 6 км.

Марш­рут A — B — D — C, длина 5 км.

 

Любые дру­гие марш­ру­ты будут длин­нее марш­ру­та A — B — D — C. Таким об­ра­зом, крат­чай­шее рас­сто­я­ние между пунк­та­ми A и C со­став­ля­ет 5 км.

 

Пра­виль­ный ответ ука­зан под но­ме­ром 2.

Ответ: 2

1157

2

Источник: СтатГрад: Ре­пе­ти­ци­он­ная работа по ин­фор­ма­ти­ке 24.02.15 ва­ри­ант ИН90502.

55. За­да­ние 3 № 1216. Между населёнными пунк­та­ми A, B, C, D по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых (в ки­ло­мет­рах) при­ве­де­на в таб­ли­це.

	A	B	C	D	E	F
A		8	3
B	8			3
C	3				4	3
D		3			1	3
E			4	1		2
F			3	3	2

 

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми A и D (при усло­вии, что пе­ре­дви­гать­ся можно толь­ко по по­стро­ен­ным до­ро­гам).

1) 7

2) 8

3) 9

4) 11

По­яс­не­ние.

Найдём все ва­ри­ан­ты марш­ру­тов из A в D и вы­бе­рем самый ко­рот­кий.

 

Из пунк­та A можно по­пасть в пунк­ты B, С.

Из пунк­та B можно по­пасть в пунк­т D.

Из пунк­та C можно по­пасть в пунк­ты E, F.

Из пунк­та E можно по­пасть в пунк­ты F, D.

Из пунк­та F можно по­пасть в пункт D.

 

A — B — D: длина марш­ру­та 11 км.

A — C — E — F — D: длина марш­ру­та 13 км.

A — C — E — D: длина марш­ру­та 8 км.

A — C — F — D: длина марш­ру­та 9 км.

 

 

Ответ: 2.

Ответ: 2

1216

2

Источник: СтатГрад: Ре­пе­ти­ци­он­ная ра­бо­та по ин­фор­ма­ти­ке 28.04.15 ва­ри­ант ИН90502.

56. За­да­ние 3 № 1256. Между населёнными пунк­та­ми A, B, C, D, E по­стро­е­ны до­ро­ги, про­тяжённость ко­то­рых (в ки­ло­мет­рах) при­ве­де­на в таб­ли­це.

Опре­де­ли­те длину крат­чай­ше­го пути между пунк­та­ми B и E. Пе­ре­дви­гать­ся можно толь­ко по до­ро­гам, про­тяжённость ко­то­рых ука­за­на в таб­ли­це.

 

1) 7

2) 8

3) 9

4) 10

Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице

Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.

A

A

B

B

1

C

1

C

D

D

2

E

2

E

2

2

7

7

3

3

4

4

Ответ: 6

Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице:

Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.

A

A

B

B

5

C

C

5

3

3

D

D

1

E

E

1

4

4

6

6

1

1

Ответ: 9

Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице:

Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.

A

A

B

B

C

C

2

2

6

6

D

D

3

4

3

4

E

E

3

3

2

2

Ответ: 7