«применение основных тригонометрических тождеств для преобразования выражений»

Тема : «ПРИМЕНЕНИЕ ОСНОВНЫХ ТРИГОНОМЕТРИЧЕСКИХ ТОЖДЕСТВ ДЛЯ ПРЕБРАЗОВАНИЯВЫРАЖЕНИЙ»

Цели урока:

Обучающие:

• уметь находить четверть и знак тригонометрических функций;

• умение переводить радианную меру угла в градусную меру;

• уметь использовать основные формулы тригонометрии при упрощении тригонометрических выражений;

• уметь пользоваться соотношениями между сторонами и углами в прямоугольном треугольнике;

Развивающие:

• интеллектуальное, эмоциональное, личностное развитие ученика;

• организовывать себя на работу, пользоваться умением самопроверки;

• развивать познавательный интерес;

• познакомить с историей возникновения тригонометрии;

• вызвать интерес к урокам математики;

Воспитательные:

• воспитывать настойчивость и упорство в достижении цели;

• показать красоту математики;

• эстетическое воспитание осуществляется через формирование умения рационально, аккуратно оформлять задание в тетради, через наглядные и дидактические пособия.

Базовые знания:

• основные формулы тригонометрии;

• формулы приведения;

• понятие синуса, косинуса, тангенса, котангенса;

• радианная мер угла, градусная мера угла;

• единичная окружность;

• число «пи».

Тип урока: Урок совершенствования и закрепления знаний.

Формы учебной работы: индивидуально-коллективная (группами).

Оборудование:; таблица значений тригонометрических функций; рабочие тетради;

Ход урока

I. Организационный момент. Приветствие.

Здравствуйте! Я очень рада всех вас видеть, надеюсь, что это взаимно, и в доказательство оного улыбнемся, друг другу и начнём урок.

При этом мы должны будем применить знания с прошлых уроков. В тетрадях записываем число и тему занятия:«ПРИМЕНЕНИЕ ОСНОВНЫХ ТРИГОНОМЕТРИЧЕСКИХ ТОЖДЕСТВ ДЛЯ ПРЕБРАЗОВАНИЯВЫРАЖЕНИЙ»

Цели урока: уметь использовать основные формулы тригонометрии при упрощении тригонометрических выражений.

III. Повторение опорных знаний.

Диктант.

Думать придётся много, записывать мало.

• Какой раздел математики вы изучаете? (тригонометрия)

• Абсцисса точки, лежащей на единичной окружности называется(косинусом)

• Ордината точки, лежащей на единичной окружности называется (синусом)

• sin2= ? sin0=? Cosπ/2=? cosπ/4=? sinπ/6=?

• Отношение синуса к косинусу – это (тангенс).

• основное тригонометрическое тождество (sin²x + cos²x = 1)

• как можно еще представить «1» в виде других тригонометрических функций?

• Математика – мой любимый предмет. (да/нет)

IV. Обобщение и систематизация.

Основные тригонометрические тождества.

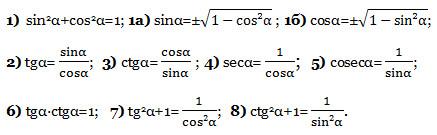
secα читают: «секанс альфа». Это число, обратное косинусу альфа.

соsecα читают: «косеканс альфа». Это число, обратное синусу альфа.

sin²x + cos²x = 1 (1)

sinx/cosx = ctgx

1-sin²x = cos²x (2)

tgx·ctx = 1 (3)

sin²x – 1 = -cos²x (4)

sin(-x) = sinx

1 + tg²x = 1 / sin²x

Примеры. Упростить выражение:

а) 1 – sin²α; б) cos²α – 1; в) (1 – cosα)(1+cosα);

 г) sin²αcosα – cosα; д) sin²α+1+cos²α;

е) sin⁴α+2sin²αcos²α+cos⁴α; ж) tg²α – sin²αtg²α;

 з) ctg²αcos²α – ctg²α; и) cos²α+tg²αcos²α.

Решение.

а) 1 – sin²α = cos²α по формуле 1);

б) cos²α – 1 =- (1 – cos²α) = -sin²α также применили формулу 1);

в) (1 – cosα)(1+cosα) = 1 – cos²α = sin²α. Вначале мы применили формулу разности квадратов двух выражений: (a – b)(a+b) = a² – b², а затем формулу 1);

г) sin²αcosα – cosα. Вынесем общий множитель за скобки.

sin²αcosα – cosα = cosα(sin²α – 1) = -cosα(1 – sin²α) = -cosα ∙ cos²α = -cos³α. Вы, конечно, уже заметили, что так как 1 – sin²α = cos²α, то sin²α – 1 = -cos²α. Точно так же, если 1 – cos²α = sin²α, то cos²α – 1 = -sin²α.

д) sin²α+1+cos²α = (sin²α+cos²α)+1 = 1+1 = 2;

е) sin⁴α+2sin²αcos²α+cos⁴α. Имеем: квадрат выражения sin²α плюс удвоенное произведение sin²α на cos²α и плюс квадрат второго выражения cos²α. Применим формулу квадрата суммы двух выражений: a²+2ab+b²=(a+b)². Далее применим формулу1). Получим:  sin⁴α+2sin²αcos²α+cos⁴α = (sin²α+cos²α)² = 1² = 1;

ж) tg²α – sin²αtg²α = tg²α(1 – sin²α) = tg²α ∙ cos²α = sin²α. Применили формулу 1), а затем формулу 2).

Запомните: tgα ∙ cosα = sinα.

Аналогично, используя формулу  

3) можно получить: ctgα ∙ sinα = cosα. Запомнить!

з) ctg²αcos²α – ctg²α = ctg²α(cos²α – 1) = ctg²α ∙ (-sin²α) = -cos²α.

и) cos²α+tg²αcos²α = cos²α(1+tg²α) = 1. Мы вначале вынесли общий множитель за скобки, а содержимое скобок упростили по формуле 7).

Преобразовать выражение:

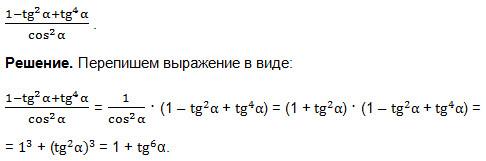
Мы применили формулу 7) и получили произведение суммы двух выражений на неполный квадрат разности этих выражений – формулу суммы кубов двух выражений:

a³ + b³ = (a + b)(a² – ab + b²). У нас а = 1, b = tg²α.

Упростить:

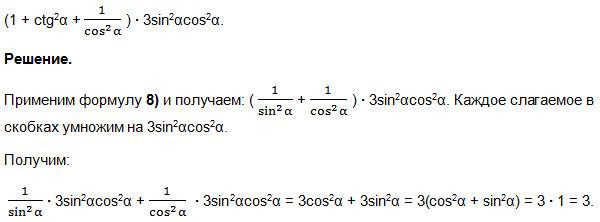
VI. Домашнее задание.

• Реферат на тему: «Математические достижения в книге Рекордов Гиннеса».

• Повторить основные тригонометрические тождества и свойства тригонометрических функций.

• Повторить знаки тригонометрических функций в зависимости от принадлежности к четвертям.

VII. Подведение итогов.

ВСЕМ БОЛЬШОЕ СПАСИБО ЗА УРОК!