Решение
иррациональных
неравенств
Цель урока
- Познакомится с методами решения иррациональных неравенств
Устная работа
- 1.Какие из следующих уравнений являются иррациональными:
- 2.Найдите область определения:
- 3.Объясните, почему эти уравнения не имеют решения на множестве действительных чисел.
Повторение изученного
(проверочная работа)
Ответы: 1. х = 83
2. х = 0
3. х = 1
Древнегреческий ученый-исследователь,
который впервые доказал существование иррациональных чисел
Ответьте на вопросы:
- 1. Что требуется для полученных значений переменной при решении иррациональных уравнений?
- 2. Способ, которым проводится проверка решений иррациональных уравнений.
- 3. Как называется знак корня?
- 4. Сколько решений имеет уравнение х 2 =а, если а
- 5. Как называются уравнения, в которых под знаком корня содержится переменная?
- 6. Как называется корень второй степени?
пров е рка
подстано в ка
ради к ал
но л ь
иррац и ональное
ква д ратный
0? 5.Как называется корень уравнения, который получается в результате неравносильных преобразований? 6.Корень какой степени существует только из неотрицательного числа?" width="640"
Кто впервые ввёл современное изображение корня?
о д но
н е чётной
к убический
дв а
посто р онний
чё т ной
Ответьте на вопросы:
1.Сколько решений имеет уравнение х 2 =0.
2.Корень какой степени существует из любого числа?
3.Как называется корень третей степени?
4.Сколько решений имеет уравнение х 2 =а, если а 0?
5.Как называется корень уравнения, который получается в результате неравносильных преобразований?
6.Корень какой степени существует только из неотрицательного числа?
Определение иррациональных неравенств
- Неравенства, в которых неизвестное содержится под знаком радикала, называются иррациональными
Методы решения
При решении иррациональных
неравенств используются
- возведение обеих частей неравенства в одну и ту же натуральную степень,
- графический способ,
- введение новых переменных и т. д.
Правило
- при возведении обеих частей неравенства в нечётную степень всегда получается неравенство, равносильное данному неравенству;
- если обе части неравенства возводят в чётную степень, то получится неравенство, равносильное исходному только в том случае, если обе части исходного неравенства неотрицательны .
Решить неравенства
1.
2.
3 .
≥
2
≥
4.
0
5.
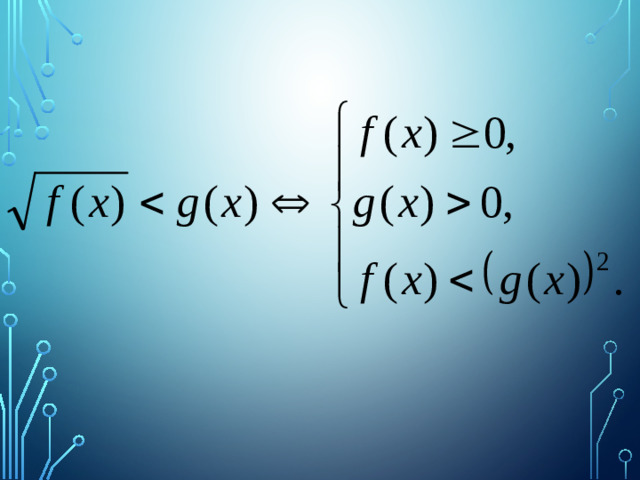
Решение задач
166(2)
167 (2,4,)
168(2)
Самостоятельная работа
166(1)
167 (1,3,)
168(1)
Ответы:
166(1) х (2 ; +∞)
167 (1,3,) 1) х (11 ; +∞) 2) х (3 ; +∞)
168(1) (- ∞ ; ) , ( ; +∞)
Домашнее задание
- П.10(1 – 5)
- 167(чёт)
- 168(2,4)
Спасибо за урок!
