
Математика уступает
Свои крепости лишь
Сильным и смелым
А.П. Конфорович
‘ Графический метод решения системы уравнений с двумя переменными’
Пластун Наталья Анатольевна

Цель урока: Научить решать систему уравнений с двумя переменными графическим методом. Рассмотреть частные случаи решения системы линейных уравнений.

Что называют системой уравнений? Рассмотрим два линейных уравнения: 1) y – 2 x = – 3 2) x + y = 3
Системой уравнений называется некоторое количество уравнений, объединенных фигурной скобкой. Фигурная скобка означает, что все уравнения должны выполняться одновременно.
y – 2 x = – 3
x + y = 3

Каждая пара значений переменных, которая одновременно является решением всех уравнений системы, называется решением системы.
Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство.
Решить систему уравнений - значит найти все её решения или установить, что их нет.
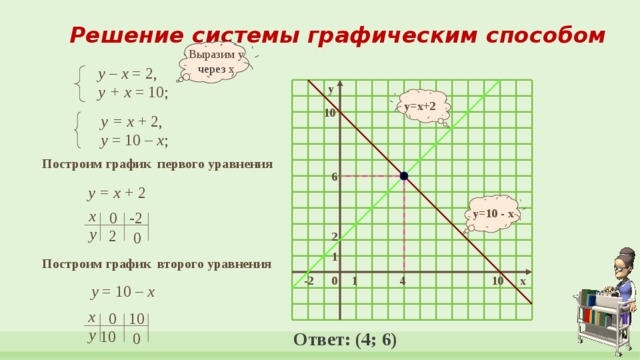
Решение системы графическим способом
Выразим у
через х
у – х = 2,
у + х = 10;
y
y=x+2
10
у = х + 2,
у = 10 – х ;
Построим график первого уравнения
6
у = х + 2
y=10 - x
х
0
-2
у
2
0
2
1
Построим график второго уравнения
4
x
10
0
1
-2
у = 10 – х
х
0
10
у
10
Ответ: (4; 6)
0

Алгоритм решения системы уравнений графическим способом
1 . Приводим оба уравнения к виду линейной функции y = k x + m.
2. Составляем расчётные таблицы для каждой функции.
3. Строим графики функций в одной координатной плоскости.
4. Определяем число решений:
- Если прямые пересекаются, то одно решение пара чисел (х ; у) – координаты точки пересечения;
- Если прямые параллельны, то нет решений;
- Если прямые совпадают, то бесконечно много решений.
5. Записываем ответ.
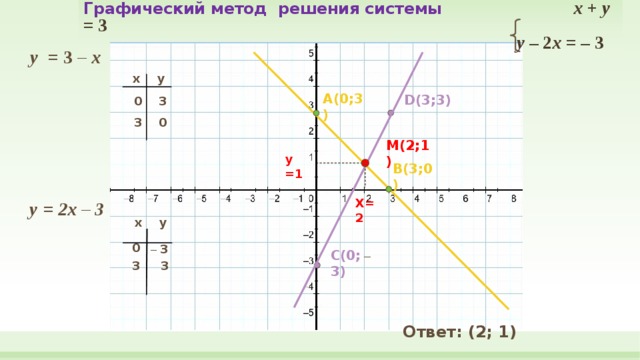
Графический метод решения системы x + y = 3 y – 2 x = – 3
у = 3 – x
x
y
A(0;3)
D(3;3)
3
0
0
3
M(2;1)
у =1
B(3;0)
X=2
у = 2x – 3
y
x
0
– 3
C(0; – 3)
3
3
Ответ: (2; 1)
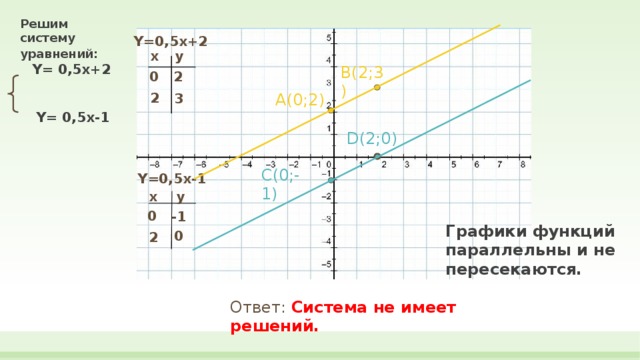
Решим систему уравнений: Y= 0,5x+2 Y= 0,5x-1
Y=0,5x+2
x
y
B(2;3)
0
2
2
A(0;2)
3
D(2;0)
C(0;-1)
Y=0,5x-1
y
x
0
-1
Графики функций параллельны и не пересекаются.
0
2
Ответ: Система не имеет решений.
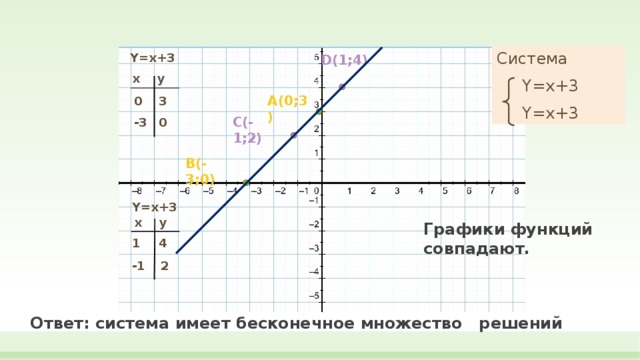
Система
Y=x+3
Y=x+3
Y=x+3
D(1;4)
x
y
A(0;3)
3
0
C(-1;2)
0
-3
B(-3;0)
Y=x+3
y
x
Графики функций совпадают.
4
1
2
-1
Ответ: система имеет бесконечное множество решений
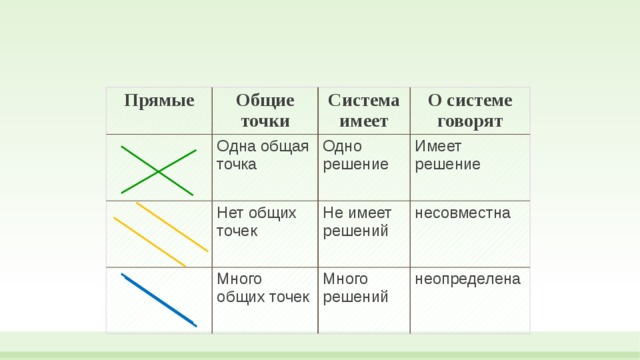
Прямые
Общие точки
Одна общая точка
Система имеет
Нет общих точек
Одно решение
О системе говорят
Много общих точек
Имеет решение
Не имеет решений
Много решений
несовместна
неопределена
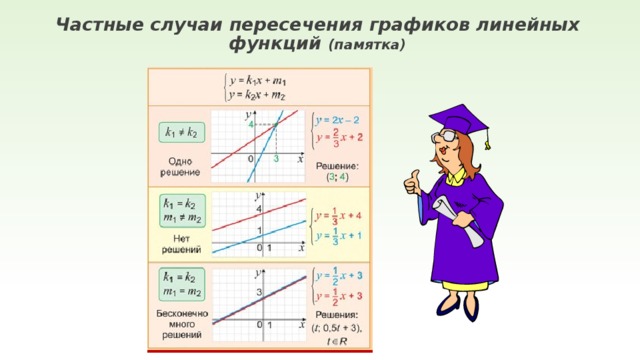
Частные случаи пересечения графиков линейных функций (памятка)

Решите систему уравнений графическим способом
1 вариант
2 вариант
у = 2 х - 3
у = 3 х - 4
у = - х + 3
у = 0,5 х + 1

У = 2х - 3
У = - х + 3
У = 0,5 х + 1
У = 3 х - 4
.
у
у
.
.
.
.
.
В(2;2)
.
А(2;1)
.
х
х
.
.
Ответ: В ( 2; 2)
Ответ: А ( 2; 1)
вывод: 1) угловые коэффициенты не равны ,
2) прямые пересекаются.

Графический способ
решения систем уравнений
1) Решите систему уравнений :
у
1) 3 х +2 у = 7,
2) 2 х + 4 у = 2,
у = 0,5 – 0,5 х
у = -1,5 х + 3,5 х у
1 2
х у
3 -1
1 0
3 -1
4
3
2
1
1
3
х
1
2
Ответ: х = 3, у = -1.

Графический способ
решения систем уравнений
2 ) Решите систему уравнений :
у
2) 2 х + у = 4,
1) х – у = -1,
у = х + 1
у = 4 - 2 х
х у
х у
0 1
0 4
2 3
2 0
4
3
2
1
1
1
х
2
3
Ответ: х = 1, у = 2.

Домашнее задание:
1. Решите с помощью графиков систему уравнений:
2 . Подберите если возможно, такое значение к , при котором данная система имеет единственное решение; не имеет решений; имеет бесконечное множество решений: а) б) в)
- Научился ли я решать систему графическим методом;
- понял ли я алгоритм решения систем линейных уравнений графическим методом;
- смогу ли я использовать при решении частные случаи;
- могу ли я по виду системы узнать о количестве решений системы.
2
1
4
3

Спасибо за урок






