Урок геометрии в 11 классе

Тест по теме: «Цилиндр. Площадь его поверхности»

Вопрос №1: Какая фигура является основанием цилиндра?
а) Овал
б) Круг
в) Квадрат

Вопрос №2 : Чему равна площадь основания цилиндра с радиусом 2см?
а) 4 π
б) 8 π
в) 4
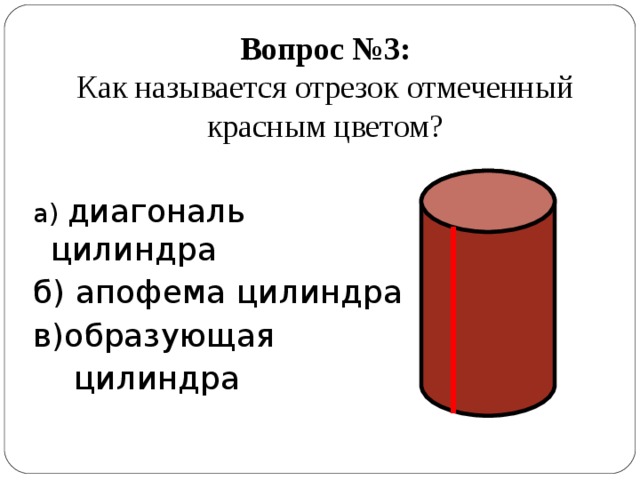
Вопрос №3: Как называется отрезок отмеченный красным цветом?
а) диагональ цилиндра
б) апофема цилиндра
в)образующая
цилиндра

Вопрос №4: По какой формуле можно вычислить боковую поверхность цилиндра?
а ) 2 π Rh
б) 2 π R(h+R)
в) π R 2 h

Вопрос № 5 : По какой формуле можно вычислить полную поверхность цилиндра?
а) π R 2 h
б) 2 π Rh
в) 2 π R(h+R)

3см
5см
3см
Вопрос №6: Вычислите боковую поверхность данного цилиндра.
а) 15 π см 2
б) 30 π см 2
в) 48 π см 2
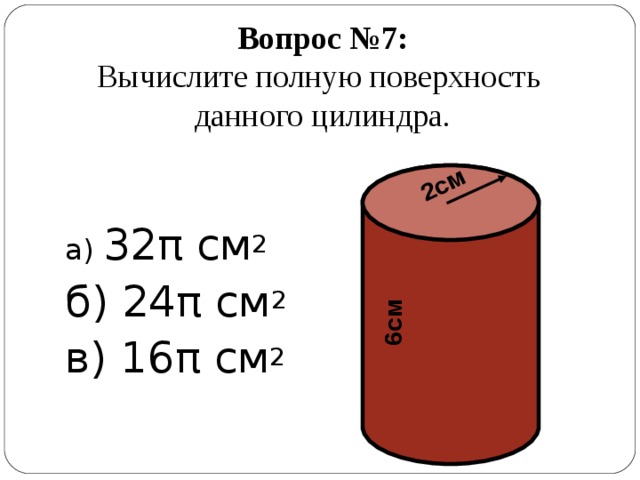
2см
6см
Вопрос №7: Вычислите полную поверхность данного цилиндра.
а) 32 π см 2
б) 24 π см 2
в) 16 π см 2

Вопрос № 8 : Чему равна площадь осевого сечения цилиндра радиуса 1см и образующей 3см?
а) 6 см 2
б) 3 см 2
в) 6 π см 2
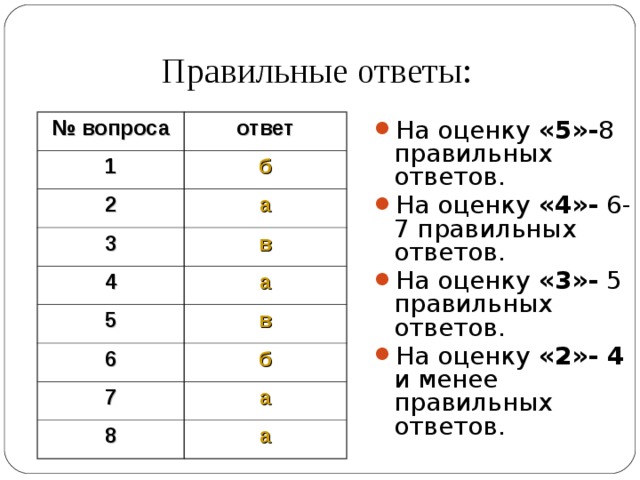
Правильные ответы:
- На оценку «5»- 8 правильных ответов.
- На оценку «4»- 6 - 7 правильных ответов.
- На оценку «3»- 5 правильных ответов.
- На оценку «2»- 4 и менее правильных ответов.
№ вопроса
ответ
1
б
2
а
3
в
4
5
а
в
6
б
7
а
8
а

«... Читал я где-то, что царь однажды воинам своим велел снести земли по горсти в кучу. И гордый холм возвысился, и царь мог с высоты с весельем озирать и дол, покрытый белыми шатрами, и море, где бежали корабли.» А.С. Пушкин «Скупой рыцарь»

Тема урока:

Цели урока :
Познакомить с понятием конуса, с историей развития представлений о конусе.
Сформировать навык решения задач по нахождению элементов конуса.
Показать возможность применения конуса в различных областях
Воспитание познавательной активности, культуры общения, культуры диалога.
Развитие математически грамотной речи, логического мышления, сознательного восприятия учебного материала.

Конус в переводе с греческого «konos» означает
«сосновая шишка».
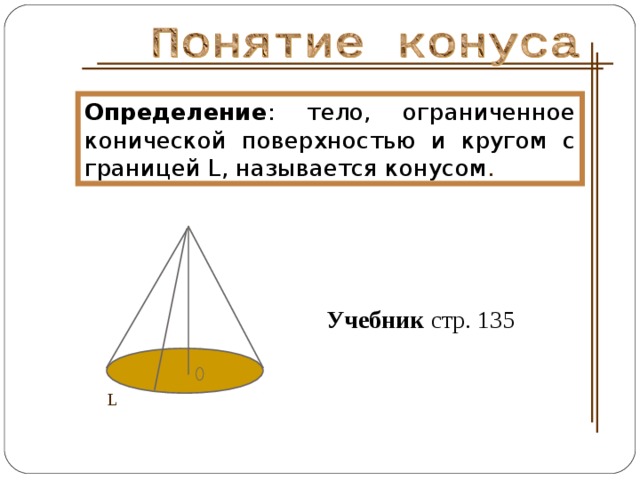
Определение : тело, ограниченное конической поверхностью и кругом с границей L , называется конусом .
Учебник стр. 135
L
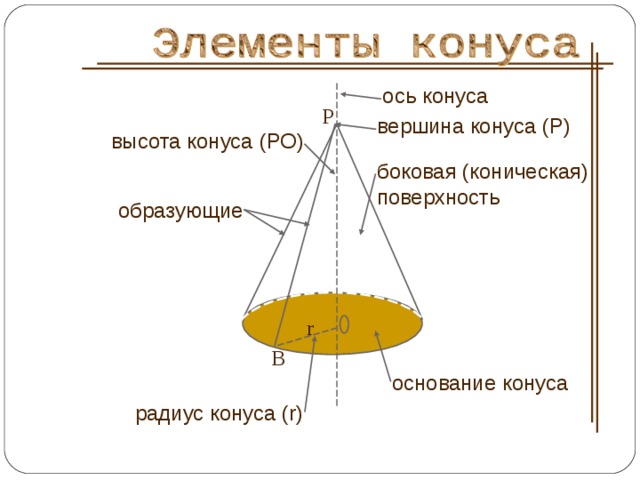
ось конуса
P
вершина конуса (Р)
высота конуса ( РО )
боковая (коническая) поверхность
образующие
r
B
основание конуса
радиус конуса ( r )

Конусы вокруг нас

Карликовое дерево

Конусообраз-ные дома - трулли

Мороженное

Оградительные конусы

Туфовые дома (высечены в скале)

Кусты в королевском саду

Конусы - ракушки

Крыша-конус

Надувные конусы

Палатка

Конус – тело вращения
Конус получается при вращении прямоугольного треугольника вокруг катета
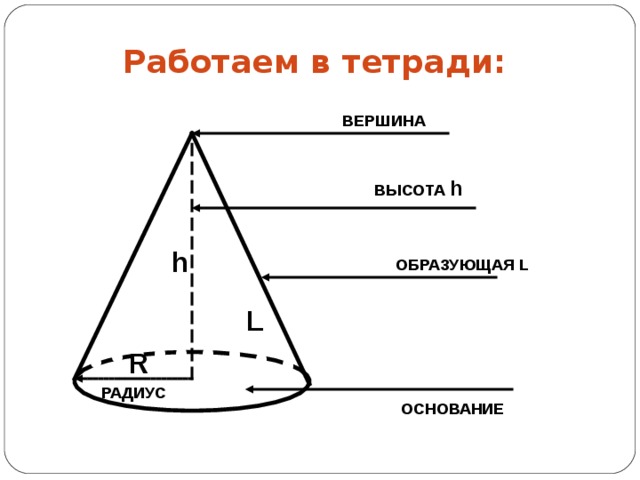
Работаем в тетради:
ВЕРШИНА
ВЫСОТА h
h
ОБРАЗУЮЩАЯ L
L
R
РАДИУС
ОСНОВАНИЕ
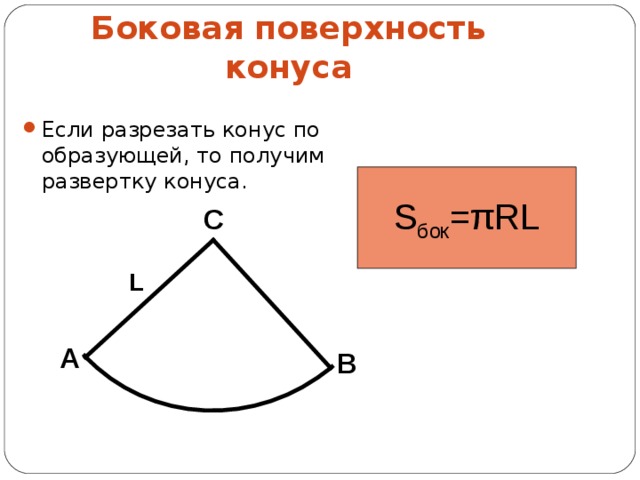
Боковая поверхность конуса
- Если разрезать конус по образующей, то получим развертку конуса.
S бок = π RL
C
L
A
B
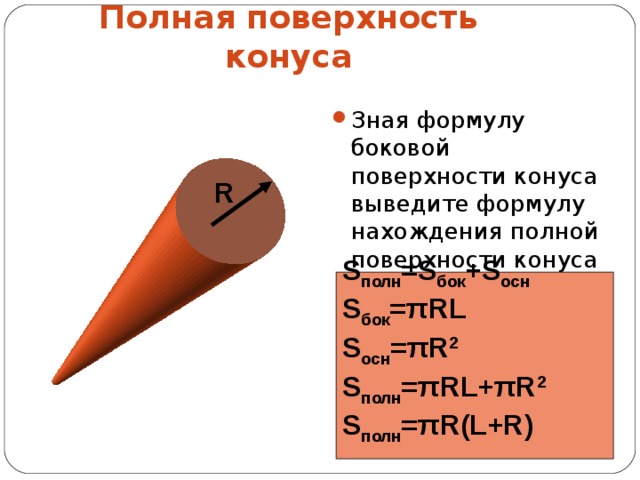
Полная поверхность конуса
- Зная формулу боковой поверхности конуса выведите формулу нахождения полной поверхности конуса
R
S полн =S бок +S осн
S бок = π RL
S осн = π R 2
S полн = π RL+ π R 2
S полн = π R(L+R)
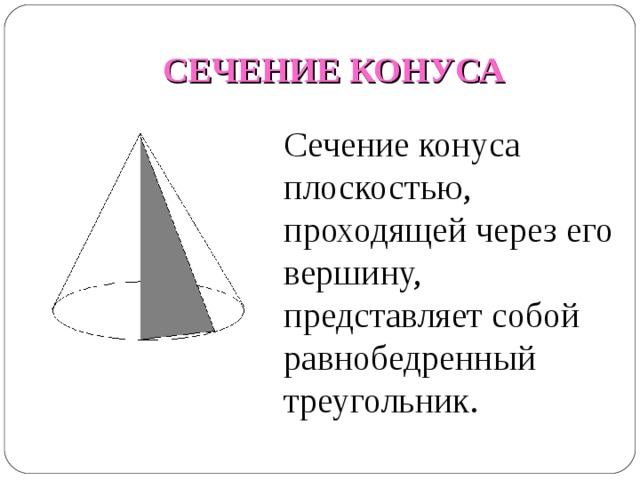
СЕЧЕНИЕ КОНУСА
Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник.

СЕЧЕНИЕ КОНУСА
Осевое сечение конуса-это сечение, проходящее через его ось.
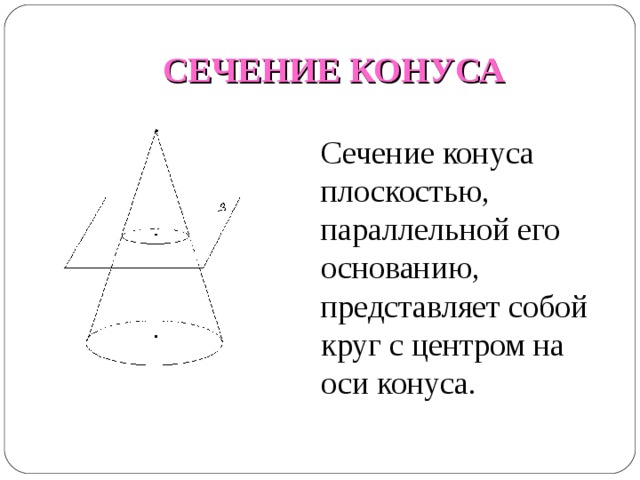
СЕЧЕНИЕ КОНУСА
Сечение конуса плоскостью, параллельной его основанию, представляет собой круг с центром на оси конуса.
Образующая L
Высота h
Радиус R
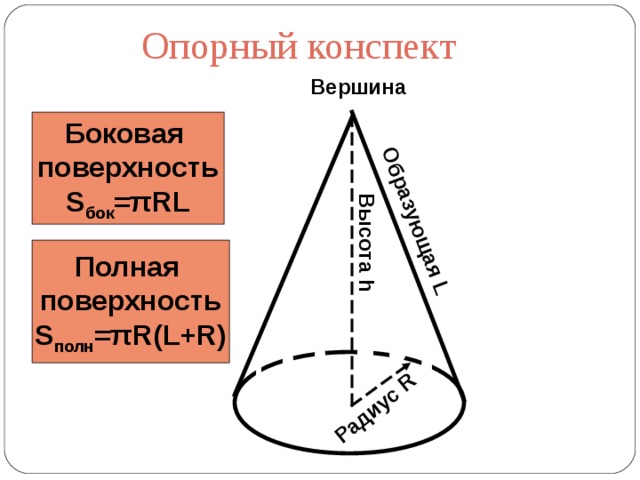
Опорный конспект
Вершина
Боковая
поверхность
S бок = π RL
Полная
поверхность
S полн = π R(L+R)

Источники:
- Учебник «Геометрия 10-11» под ред. Л.С.Атанасян 2012
- 900igr.net





