Презентация на тему: “ П ризма ”

- Многогранник, составленный из двух равных многоугольников A 1 A 2 …A n и B 1 B 2 …B n , расположенных в параллельных плоскостях, и n параллелограммов, называется призмой
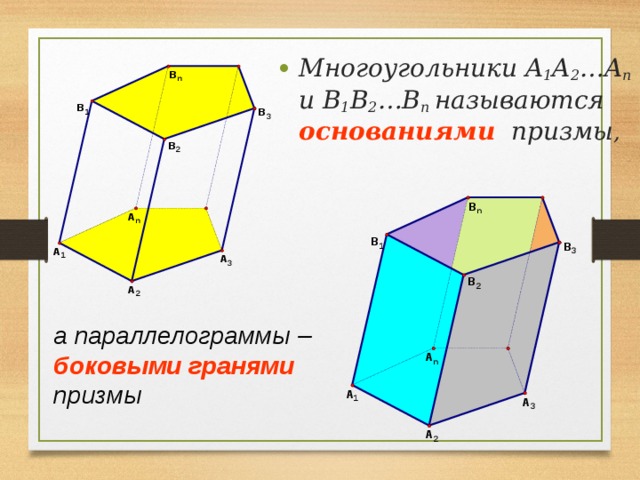
- Многоугольники A 1 A 2 …A n и B 1 B 2 …B n называются основаниями призмы ,
а параллелограммы – боковыми гранями призмы
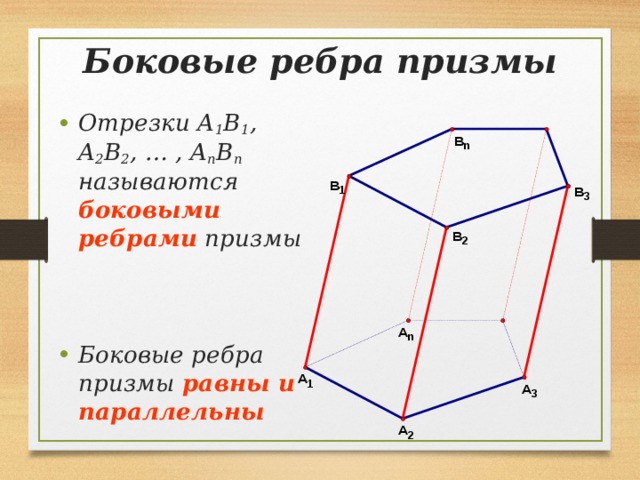
Боковые ребра призмы
- Отрезки A 1 B 1 , A 2 B 2 , … , A n B n называются боковыми ребрами призмы
- Боковые ребра призмы равны и параллельны
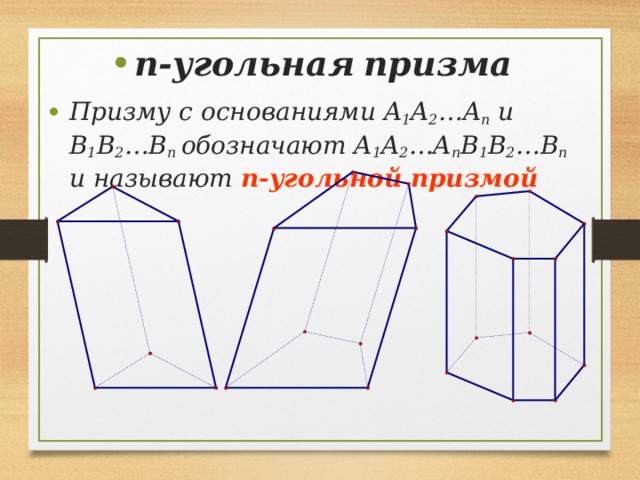
- n-угольная призма
- Призму с основаниями A 1 A 2 …A n и B 1 B 2 …B n обозначают A 1 A 2 …A n B 1 B 2 …B n и называют n-угольной призмой
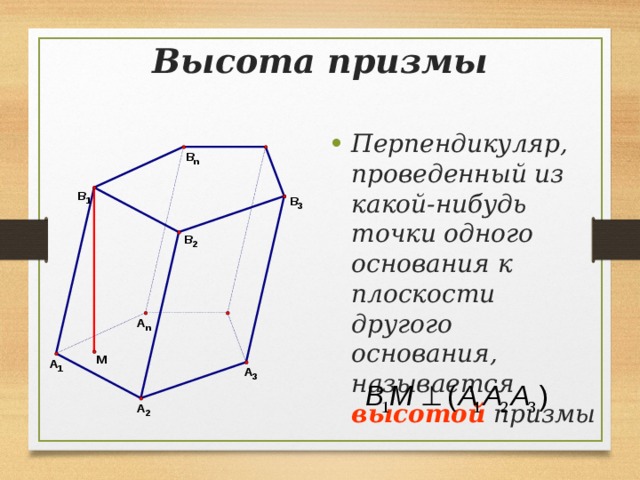
Высота призмы
- Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы
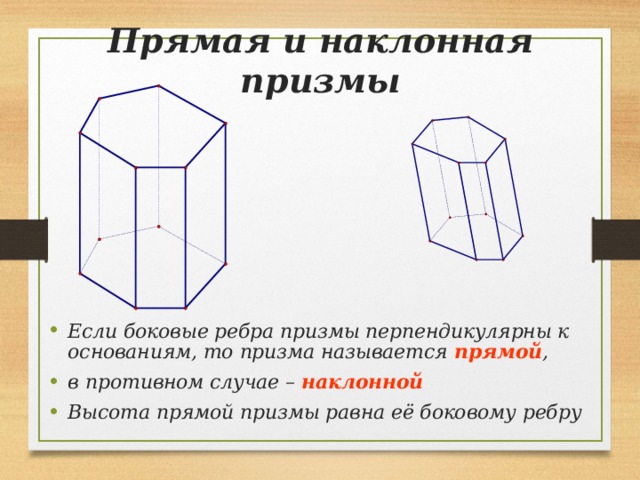
Прямая и наклонная призмы
- Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой ,
- в противном случае – наклонной
- Высота прямой призмы равна её боковому ребру

Правильная призма
- Прямая призма называется правильной , если её основания – правильные многоугольники
- У правильной призмы все боковые грани – равные прямоугольники
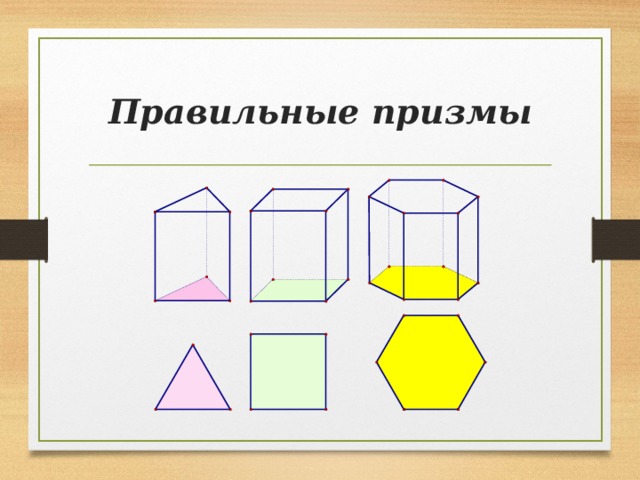
Правильные призмы
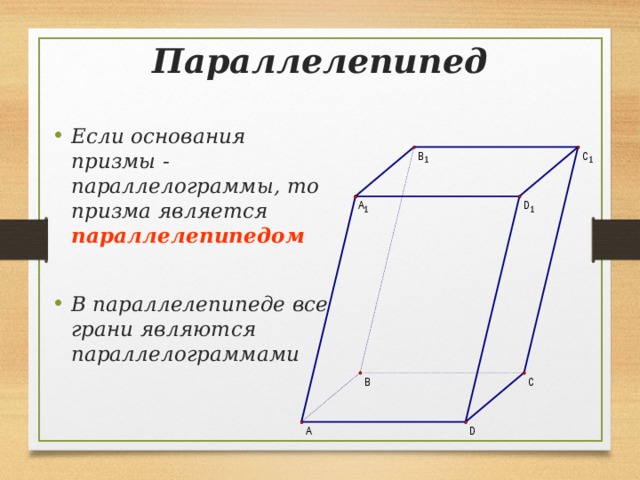
Параллелепипед
- Если основания призмы - параллелограммы, то призма является параллелепипедом
- В параллелепипеде все грани являются параллелограммами
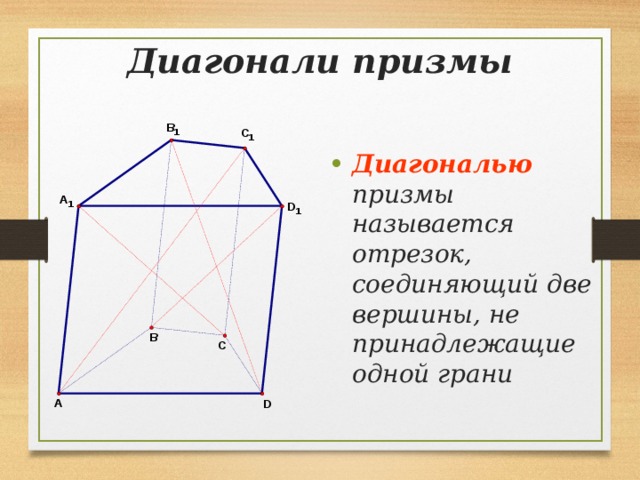
Диагонали призмы
- Диагональю призмы называется отрезок, соединяющий две вершины, не принадлежащие одной грани
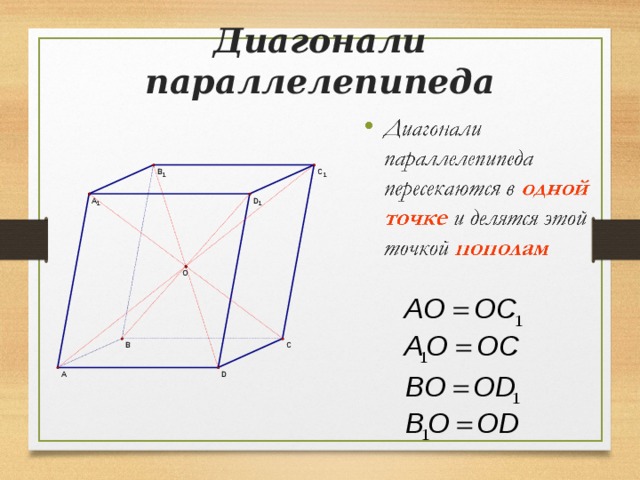
Диагонали параллелепипеда
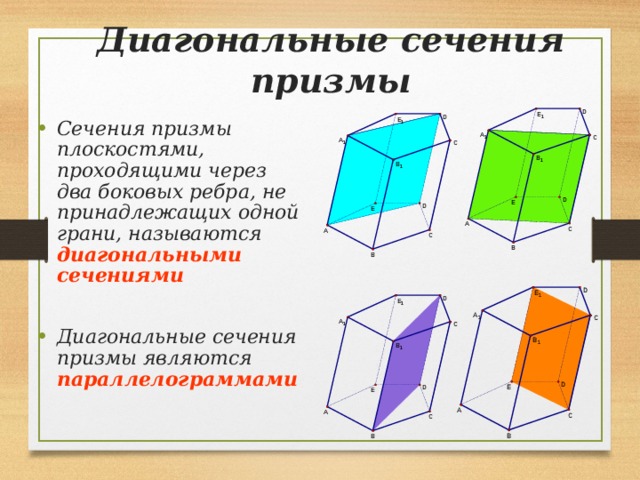
Диагональные сечения призмы
- Сечения призмы плоскостями, проходящими через два боковых ребра, не принадлежащих одной грани, называются диагональными сечениями
- Диагональные сечения призмы являются параллелограммами
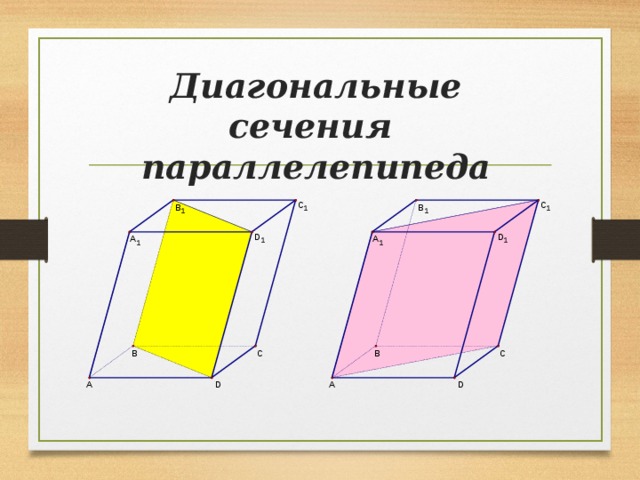
Диагональные сечения параллелепипеда

Площадь поверхности призмы
- Площадью полной поверхности призмы называется сумма площадей всех её граней
- Площадью боковой поверхности призмы называется сумма площадей её боковых граней

Теорема о площади боковой поверхности прямой призмы
Теорема .
Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы
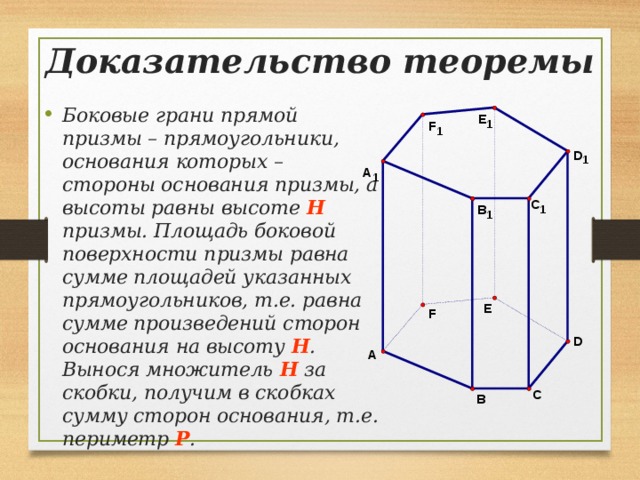
Доказательство теоремы
- Боковые грани прямой призмы – прямоугольники, основания которых – стороны основания призмы, а высоты равны высоте H призмы. Площадь боковой поверхности призмы равна сумме площадей указанных прямоугольников, т.е. равна сумме произведений сторон основания на высоту H . Вынося множитель H за скобки, получим в скобках сумму сторон основания, т.е. периметр P .


Fin?





