Презентация к уроку алгебры в 9 классе по теме "Степенная функция"

Тема нашего урока: функции и графики Цель урока: графическое решение задач.

Девиз урока

«КНИГА – КНИГОЙ, А МОЗГАМИ ДВИГАЙ» (В. В.Маяковский).

Задачи урока

Повторить и закрепить умения:

• Строить и читать графики степенной функции;
• Графически решать уравнения, неравенства, системы.

Найти область определения функции:

а) (-  ; 1,5);

б)(-  ; -4 ]  ( 5 ;+  )

в)(-  ; -2 ]  [0.5 ;+  )

г) ( -  ; +  );

1.

2.

3.

4.

На доске группы показывают решение. После проверки показываю правильные ответы.

3

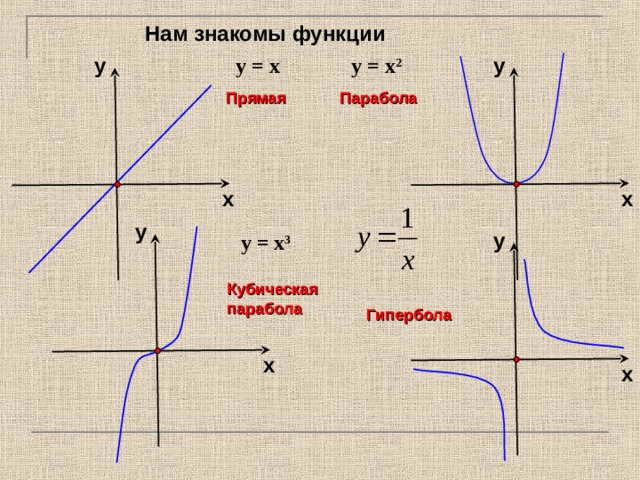
Нам знакомы функции

• Нам знакомы функции
• Нам знакомы функции
• Нам знакомы функции
• Нам знакомы функции

у

у = х 2

у

у = х

Прямая

Парабола

х

х

у

у

у = х 3

Кубическая

парабола

Гипербола

х

х

у = х, у = х 2 , у = х 3 ,

• у = х, у = х 2 , у = х 3 ,
• у = х, у = х 2 , у = х 3 ,
• у = х, у = х 2 , у = х 3 ,
• у = х, у = х 2 , у = х 3 ,

Все эти функции являются частными случаями степенной функции

• Все эти функции являются частными случаями степенной функции
• Все эти функции являются частными случаями степенной функции
• Все эти функции являются частными случаями степенной функции
• Все эти функции являются частными случаями степенной функции

у = х n , у = х - n где n – заданное натуральное число

Свойства и график степенной функции зависят от значения показателя n

• Свойства и график степенной функции зависят от значения показателя n
• Свойства и график степенной функции зависят от значения показателя n
• Свойства и график степенной функции зависят от значения показателя n
• Свойства и график степенной функции зависят от значения показателя n

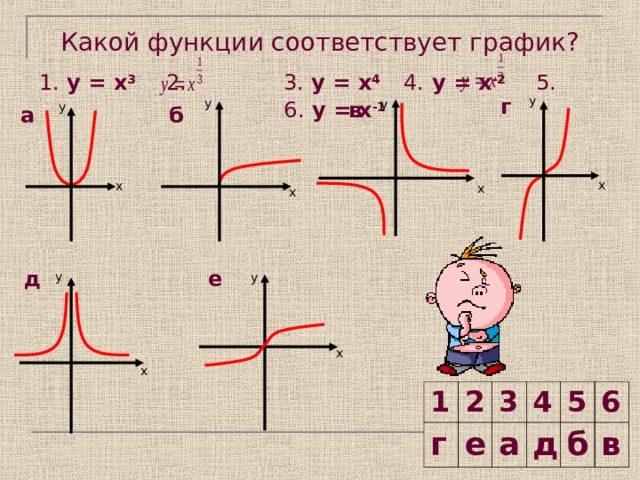
Какой функции соответствует график? 1. у = х 3 2. 3. у = х 4 4. у = х -2 5. 6. у = х -1

у

г

у

у

в

у

а

б

х

х

х

х

е

д

у

у

Индивидуальная работа: Установите какой функции соответствует график; Как записывается формула степенной функции в общем виде, график которой похож на параболу? На кубическую параболу? На гиперболу, симметричную относительно начала координат? На гиперболу, симметричную относительно оси ординат? Определите четность этих функций и монотонность. Оцените себя: все ответы правильные 3 балла, за 4-5 ответа 2 балла, за 1-3 ответа 1 балл.

х

х

1

г

2

е

3

а

4

д

5

б

6

в

5

6

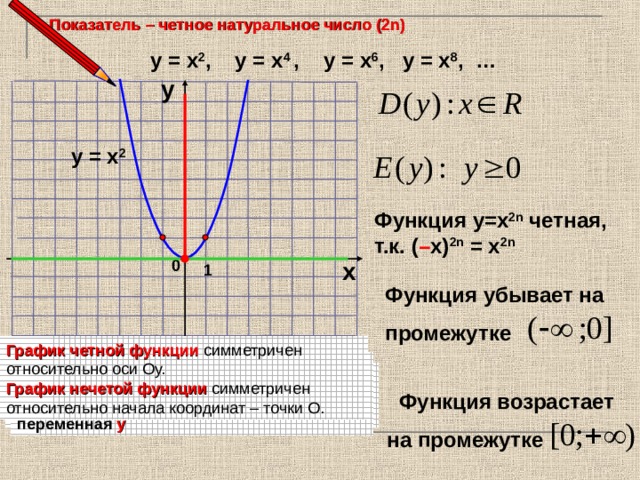
Показатель – четное натуральное число (2n)

у = х 2 , у = х 4 , у = х 6 , у = х 8 , …

у

у = х 2

Функция у=х 2 n четная,

т.к. ( – х) 2 n = х 2 n

х

0

1

Функция убывает на

промежутке

График четной функции симметричен относительно оси Оу.

График нечетой функции симметричен относительно начала координат – точки О.

Область значений функции –

множество значений,

которые может принимать

переменная у

Область определения функции –

значения, которые может принимать переменная х

Функция возрастает

на промежутке

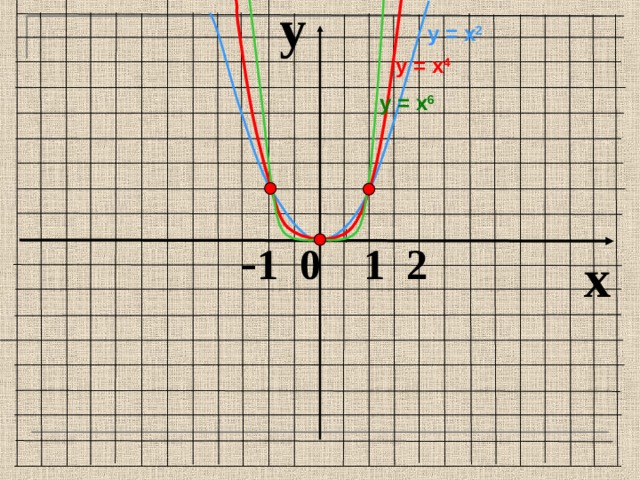
y

у = х 2

у = х 4

у = х 6

- 1 0 1 2

x

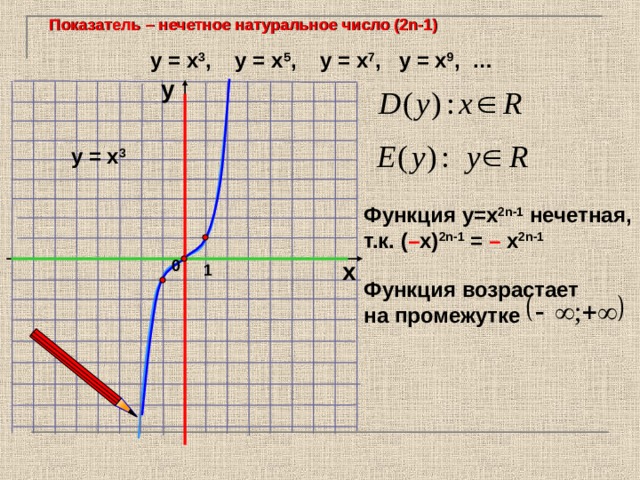
Показатель – нечетное натуральное число (2n-1)

у = х 3 , у = х 5 , у = х 7 , у = х 9 , …

у

у = х 3

Функция у=х 2 n -1 нечетная,

т.к. ( – х) 2 n -1 = – х 2 n -1

0

х

1

Функция возрастает на промежутке

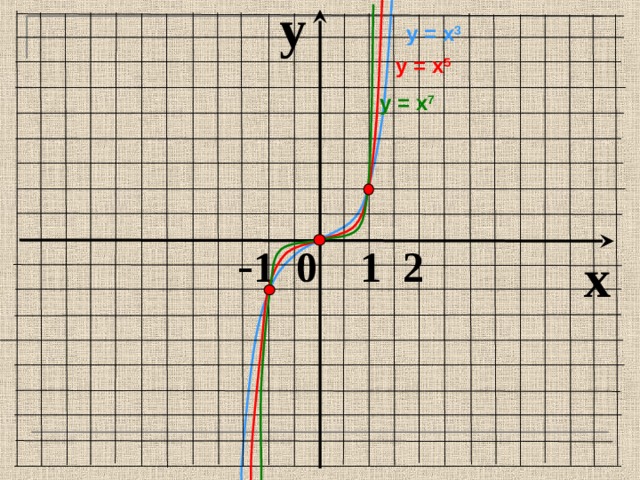
y

у = х 3

у = х 5

у = х 7

- 1 0 1 2

x

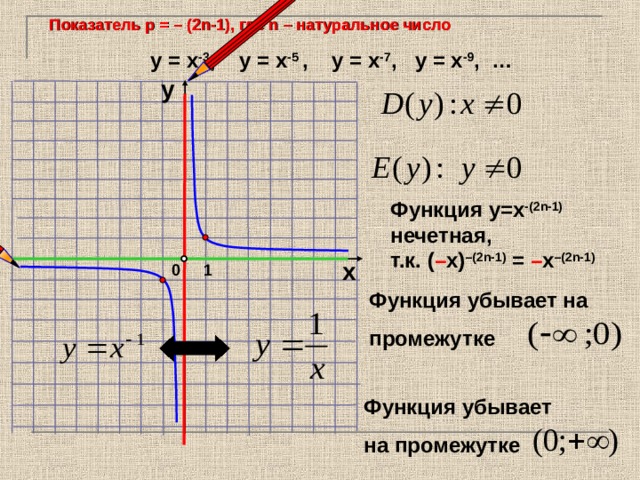
Показатель р = – ( 2n -1), где n – натуральное число

у = х -3 , у = х -5 , у = х -7 , у = х -9 , …

у

Функция у=х -(2 n -1) нечетная,

т.к. ( – х) –(2 n -1) = – х –(2 n -1)

х

0

1

Функция убывает на

промежутке

Функция убывает

на промежутке

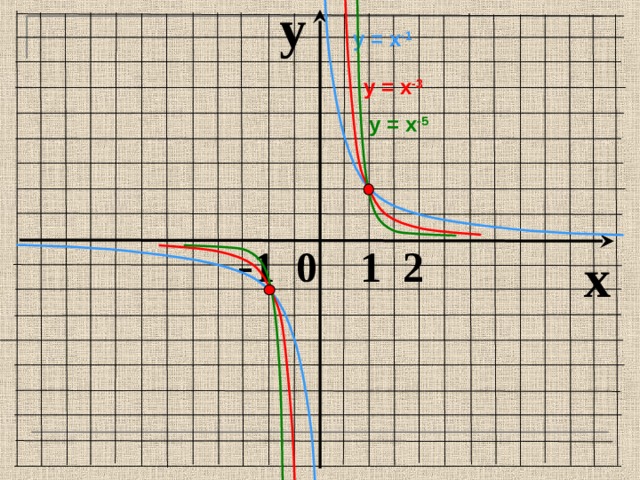
y

у = х -1

у = х -3

у = х -5

- 1 0 1 2

x

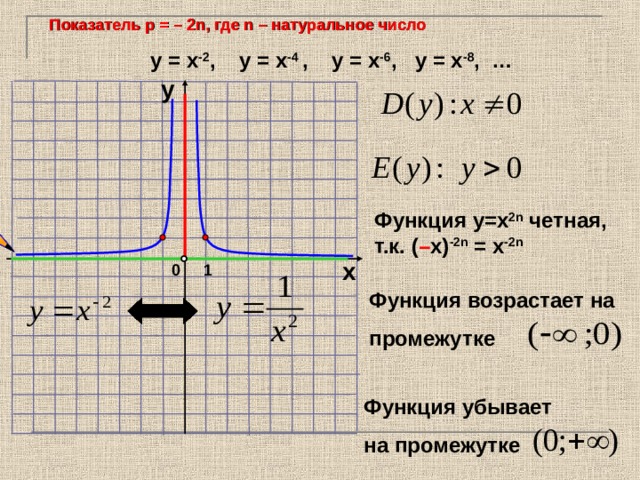
Показатель р = – 2n , где n – натуральное число

у = х -2 , у = х -4 , у = х -6 , у = х -8 , …

у

Функция у=х 2 n четная,

т.к. ( – х) -2 n = х -2 n

х

1

0

Функция возрастает на

промежутке

Функция убывает

на промежутке

Что мы должны уметь:

• Уметь строить график степенной функции.
• Уметь по графику составлять формулы функции.
• Уметь строить и читать кусочные функции.
• Уметь графически решать уравнения, неравенства и их системы.

Вы должны уметь:

13

13

СПАСИБО ЗА УРОК.

Вы должны уметь:

13

13