БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ОРЛОВСКОЙ ОБЛАСТИ
«МЕЗЕНСКИЙ ЛИЦЕЙ»
План-конспект
мастер-класса
Выполнила: учитель математики
Сопнева С. В.
2016
Подготовка к ОГЭ по математике.
Разбор типовых задач № 22.
Решение текстовых задач.
Тема: Решение текстовых задач.
Цель занятия:
научить распознавать типы текстовых задач;
систематизировать и обобщить теоретические знания по данной теме.
разобрать различные способы решения задач на движение по воде, на суше;
разобрать способы решения задач на совместную работу;
разобрать способы решения задач на смеси, сплавы и растворы;
определить уровень подготовленности учащихся к экзамену по данной теме.
Ход мастер-класса:
1 шаг. Презентация педагогического опыта.
2 шаг. Совместное решение задач.
3 шаг. Самостоятельное решение задач.
4 шаг. Рефлексия.
1 шаг. Презентация педагогического опыта.
Сообщение темы и целей мастер- класса.
Слово учителя: Текстовые задачи в математике играют очень важную роль.
Всесторонне функции задач, в том числе и текстовых, охарактеризовал Е.С. Ляпин: «Путем решения задач формируются различные математические понятия, осмысливаются различные арифметические операции. Задачи часто служат основой для вывода некоторых теоретических положений. Задачи содействуют обогащению и развитию правильной речи учащихся. Задачи помогают учащимся понять количественные соотношения различных жизненных фактов. Задачи соответствующего содержания содействуют воспитанию учащихся. Особенно важна роль задач как средства развития логического мышления учащихся, их умения устанавливать зависимости между величинами, делать правильные умозаключения».
Решая задачи, учащиеся приобретают новые математические знания, готовятся к практической деятельности. Все математические задачи появились из практического соображения. Ещё в далёком прошлом одним из стимулов изучения математики была потребность зарождающегося строительства и, возникшей вслед за ним, архитектуры
Любая текстовая задача состоит из двух частей: условия и требования (вопроса). В условии соблюдаются сведения об объектах и некоторых величинах, характеризующих данные объекта, об известных и неизвестных значениях этих величин, об отношениях между ними. Требования задачи – это указание того, что нужно найти. Оно может быть выражено предложением в повелительной или вопросительной форме. В наше время существует огромное множество задач, но из них выделяют три основных типа: задачи на движение, процентное содержание и на работу.
Как правильно решать текстовые задачи? Я всегда говорю детям, чтобы правильно и быстро решить задачу, необходимо для себя выделить три этапа решения.
Три основных этапа успешного решения текстовых задач
Первый этап: моделирование ситуации, описанной в условии задачи. Итак, вы прочитали текст задачи. Не торопитесь сразу ее решать. Во-первых, запишите подробно условие. Если перед вами задача на движение, в которой, например, фигурирует автомобиль и велосипед, то я предлагаю учащимся составить таблицу вида
|
| v (скорость) | t (время) | S (расстояние) |
| Велосипед |
|
|
|
| Автомобиль |
|
|
|
В эту таблицу нужно занести все, что дано в условии задачи. Этот этап решения, на котором записывается краткое условие, является самым важным этапом, поэтому основная масса времени должна уходить именно на него. Нужно перевести все словесные данные на математический язык, и в этом деле самое главное – не экономить бумагу! При выборе неизвестных, необходимо, чтобы неизвестных было как можно меньше.
Второй этап: составление и решение уравнения. До составления уравнения, приводим (если надо) все величины задачи к единым единицам измерения. Если краткое условие записано грамотно и понятно, то составить уравнение очень легко, нужно только понять, что требуется – сложить некоторые величины (выраженные через x или другие неизвестные), чтобы получить данную в тексте суммарную величину или вычесть из одной величину другую, если в тексте дана разница между ними. Результатом решения уравнения является нахождение неизвестной или нескольких неизвестных. Далее выполните отбор корней.
Третий этап: составление ответа. Некоторые ученики пишут, не думая, в ответ то число, которое они нашли в процессе решения уравнения, но это не всегда правильно. Иногда требуется провести дополнительные расчеты, чтобы получить именно то, о чем спрашивается в задаче.
При правильном и последовательном выполнении этих трех пунктов решение текстовой задачи становится чисто механической работой, для выполнения которой не нужно по сто раз перечитывать текст задачи, надеясь получить неожиданное творческое озарение.
Итак, рассмотрим основные виды текстовых задач, которые встречаются в части 2 ОГЭ.
Задачи на движение
Уравнения, которые составляются на основании условий задач на движение, обычно содержат такие величины, как расстояние, скорости движущихся объектов, время, а также скорость течения воды (при движении по реке). При решении этих задач принимают следующие допущения:
Если нет специальных оговорок, то движение считается равномерным.
Повороты движущихся тел, переходы на новый режим движения считаются происходящими мгновенно.
Если тело с собственной скоростью х движется по реке, скорость течения которой равна у, то скорость движения тела по течению считается равной (х + у), а против течения – (х – у).
При решении задач на движение рекомендуется сделать рисунок, отображающий все условия задачи. При этом решающий задачу должен выбрать схему решения: какого вида уравнения составлять, то есть что сравнивать: время, затраченное на движение на отдельных участках пути, или пройденный каждым объектом путь.
При решении задач такого типа часто необходимо узнать время встречи двух объектов, начинающих движение одновременно из двух точек с разными скоростями и движущихся навстречу друг другу либо в случае, когда один объект догоняет другой.
Пусть расстояние между точками А и В равно S. Два тела начинают движение одновременно, но имеют разные скорости v1 и v2. Пусть С – точка встречи, а t – время движения тел до встречи. В случае движения навстречу друг другу имеем АС = v1t, BC = v2t. Сложим эти два равенства: АС + СВ = v1t + v2t = (v1 + v2)t. AB = S = (v1 + v2)t. Если одно тело догоняет другое, то теперь получаем АС = v1t, BC = v2t. Вычтем эти равенства: АС – ВС = (v1 – v2)t. Так как АС – ВС = AB = S, то время, через которое первое тело догонит второе, определяется равенством t=S/(v1-v2)
Задачи на совместную работу
Рассмотрим еще один тип задач – задачи на совместную работу. В таких задачах обычно какую либо работу выполняют несколько человек или механизмов, работающих с постоянной для каждого из них производительностью. Правила решения задач на работу очень просты. Сначала желательно рассмотреть алгоритм решения задачи (например, при помощи таблицы).
|
| A(работа) | p(производительность) | t (время) |
|
|
|
|
|
|
|
|
|
|
A=pt
Из этой формулы легко найти t или p.
При решении таких задач возможны два случая:
Объем выполненной работы известен, т.е. если речь идет о количестве кирпичей, страниц или построенных домов — работа как раз и равна этому количеству.
Объем выполненной работы неизвестен, т.е. если объем работы не важен в задаче и нет никаких данных, позволяющих его найти — работа принимается за единицу. Построен дом (один). Написана книга (одна).
В таких задачах объем всей работы, которая должна быть выполнена, принимается за 1; время t, требующееся для выполнения всей работы, и р – производительность труда, то есть объем работы, сделанной за единицу времени, связаны соотношением
1=pt
Рассмотрим стандартную схему решения задач этого типа.
Пусть х – время выполнения некоторой работы первым рабочим,
у – время выполнения этой же работы вторым рабочим.
Тогда 1/x – производительность труда первого рабочего,
– 1\y производительность труда второго рабочего.
–1/x+1/y совместная производительность труда.
1/(1/x+1/y)– время, за которое они выполнят задание, работая вместе
Задачи на смеси и сплавы
В задачах этого типа основным является понятие «концентрация». Что же это такое?
Рассмотрим, например, раствор кислоты концентрации к процентному содержанию и наоборот весьма прост. Итак, пусть смесь в воде. Пусть в сосуде содержится 10 литров раствора, который состоит из 3 литров кислоты и 7 литров воды. Тогда относительное (по отношению ко всему объему) содержание кислоты в растворе равно 3/10=0,3. Это число и определяет концентрацию кислоты в растворе. Иногда говорят о процентном содержании кислоты в растворе. В приведенном примере процентное содержание будет таково: 30%. Как видно, переход от массы М содержит некоторое вещество массой m. Тогда:
концентрацией данного вещества в смеси (сплаве) называется величина x=m/M;
процентным содержанием данного вещества называется величина с=x*100%;
Из последней формулы следует, что при известных величинах концентрации вещества и общей массы смеси (сплава) масса данного вещества определяется по формуле m=c*M.
Задачи на смеси (сплавы) можно разделить на два вида:
Задаются, например, две смеси (сплава) с массами m1 и m2 и с концентрациями в них некоторого вещества, равными соответственно с1 и с2. Смеси (сплавы) сливают (сплавляют). Требуется определить массу этого вещества в новой смеси (сплаве) и его новую концентрацию. Ясно, что в новой смеси (сплаве) масса данного вещества равна c1m1 + c2m2, а концентрация 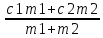 .
.
Задается некоторый объем смеси (сплава) и от этого объема начинают отливать (убирать) определенное количество смеси (сплава), а затем доливать (добавлять) такое же или другое количество смеси (сплава) с такой же концентрацией данного вещества или с другой концентрацией. Эта операция проводится несколько раз.
При решении таких задач необходимо установить контроль за количеством данного вещества и его концентрацией при каждом отливе, а также при каждом доливе смеси. В результате такого контроля получаем разрешающее уравнение.
Подготовку к ГИА-9 я провожу с помощью пособий под редакцией И. В. Ященко и сборника заданий для подготовки к государственной итоговой аттестации в 9 классе.
Подготовка к итоговой аттестации в современной школе – это комплекс учебных и воспитательных мероприятий, направленных на развитие творческих, интеллектуальных способностей учащихся, воли, трудолюбия, чувства долга и ответственности. Игнорирование одной из составляющих комплекса ведет к разрушению целостности учебного процесса, к потере интереса к учению, плохой успеваемости и деградированною личности. А сможет ли такой поврежденный человек нормально существовать и трудиться в нашем обществе? Моя вторая цель – не просто хорошо сданное ГИА, а воспитание творческой, жизнеспособной личности
2 шаг. Совместное решение задач.
Слайды на презентациях.
3 шаг. Самостоятельное решение задач.
4 шаг. Рефлексия
Послушайте притчу и выполните задание.
Шел мудрец, а навстречу ему три человека, которые везли под горячим солнцем тележки с камнями для строительства храма. Мудрец остановился и задал каждому по вопросу. У первого спросил: «Что ты делал целый день?». А тот с ухмылкой ответил, что целый день возил проклятые камни. У второго мудрец спросил: «Что ты делал целый день?» И тот ответил: «А я добросовестно выполнил свою работу». А третий улыбнулся, его лицо засветилось радостно и с удовольствием ответил: «А я принял участие в строительстве храма».
Кто себя считает первым рабочим, обведите кружочком цифру 1. Кто себя считает вторым рабочим - цифру 2, если третьим - цифру 3. Попробуйте обосновать свой ответ.
1. Первый рабочий.
2. Второй рабочий.
3. Третий рабочий.





