Урок 9
ТЕМА: ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ
Цели:
Ввести понятие теоремы и доказательства теоремы;
Доказать первый признак равенства треугольников;
Научить решать задачи на применение первого признака равенства треугольников.
Ход урока
Орг. момент
I. Актуализация опорных знаний.
Вопросы к учащимся:
1. Повторить определение смежных углов и их свойство.
2. Повторить определение вертикальных углов и их свойство.
3. Вспомнить определение равных фигур, биссектрисы угла.
4. Вспомнить, какой угол называется острым, прямым, тупым.
5. Повторить определение треугольника, его элементов; определение периметра треугольника; определение равных треугольников.
Индивидуальная работа
Карточка 1
В треугольнике АВС. АВ=10 см, АС=5см а ВС=11 см. Найдите периметр треугольника АВС.
Карточка 2
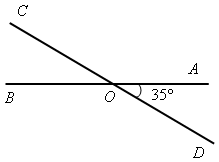
Задача. Прямые АВ и СD пересекаются в точке О так, что 
АОD =
= 35°. Найдите углы АОС и ВОС.
Групповая работа
Из данных фигур выберите, равные.
Физкультминутка
II. Объяснение нового материала.
1. Разъяснение смысла слов «теорема» и «доказательство теоремы», так как с этими понятиями учащиеся встречаются впервые.
В геометрии каждое утверждение, справедливость которого устанавливается путем рассуждений, называется теоремой, а сами рассуждения называются доказательством теоремы.
2. Напомнить учащимся, что приведенные ранее рассуждения о свойстве смежных и о равенстве вертикальных углов были доказательствами теорем, хотя мы их еще так не называли.
3. Повторить с учащимися понятие равенства фигур (отрезков, углов, треугольников)
III. Закрепление изученного материала.
Отрезки АЕ и DC пересекаются в точке В, являющейся
серединой каждого из них. а) Докажите, что ∆АВC = ∆ЕВD;
б) найдите углы А и С в ∆АВC, если в ∆ЕВD ∠D = 47°, ∠E = 42°.
Задание: найдите пары равных треугольников (см. рис. 1-2) и докажите их равенство.
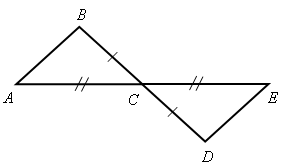
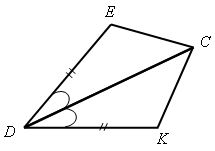
Рис. 1 Рис. 2
2. Решить задачу № 96 на доске и в тетрадях (по рис. 54).
Решение
Рассмотрим 
АОВ и DОС:
| ОА = ОD (по условию) ОВ = ОС (по условию)
углы равны) |
|
|
Тогда DСО = АВО = 74°.
АСD = АСО + DСО = 36° + 74° = 110°.
Ответ: 110°.
3. Самостоятельно учащиеся решают задачу № 1:
Из точек А и В на прямую а опущены перпендикуляры АС и ВD, причем АС = ВD.
Докажите, что АСD = ВDС.
Итоги урока.
Домашнее задание: знать доказательство первого признака равенства треугольников п. 15, решить задачи №№ 93, 94 и 95.
Карточка 1
В треугольнике АВС. АВ=10 см, АС=5см а ВС=11 см. Найдите периметр треугольника АВС.
Карточка 2
Задача. Прямые АВ и СD пересекаются в точке О так,
что АОD == 35°. Найдите углы АОС и ВОС.
1 вариант
Задание: найдите пары равных треугольников и докажите их равенство.
2 вариант
Задание: найдите пары равных треугольников и докажите их равенство.
