( ti)=а+b( ti-
)
ti а,b коэфициенттерінің мәндері ең кіші квадраттар әдісін қолдану жолымен табылады.Модельдеу әдісін болжам жасауда қолдану
Уақыт қатары мәндерінің тізбегі берілген болcын:
| Хі | Х1 | Х2 | Х3 | . . . | Хn |
| ti | t1 | t2 | t3 | . . . | tn |
Осы қатардың өзгеру тенденциясын анықтауымыз керек болсын. Осындай көріністегі мәселе – уақыт қатарын тегістеу есебі деп аталады. Бұл жерде біз негізгі өзгеретін параметрді тренд деп атаймыз. Негізгі мәселе осы трендтің уақытқа тәуелділігін анықтау болып есептеледі. Сондықтан тәуелділік мынандай көріністе болады:
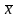( ti)=а+b( ti-
)
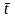мұндағы а, b – мәндері есептеп табылуы қажет болған коэфициенттері;
= 
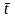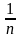
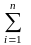ti а,b коэфициенттерінің мәндері ең кіші квадраттар әдісін қолдану жолымен табылады. Мұндағы t – аргумент, ал 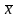(t) уақыт қатарының тренді – функция рөлін атқарады. Зерттеу жұмыстарын біз модель құру арқылы қарастырамыз:
Сызықтық модель мынаған тең: 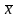(t) = а+b ( ti- 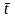), (1)
Қисық сызықты модель: 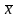(t) = а+в ( ti- 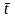)+с( ti- 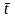)2 (2)
Прецесті адекватты түрде сипаттайтын модель түрін біз диаперсияның мәні бойынша таңдаймыз:
D =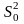 
=
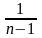
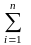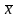( хі- )2-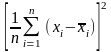 
Тренд теңдеуінің түрлері мынадай көріністе болуы мүмкін:
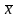(t) = а+b еct ,
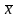(t) =а+b / t,
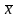(t) = а * ln t+b ,
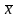(t) =а*tв ,
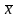(t) =at+b*t3 ,
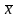(t) =а* е-в/t .
Тренд теңдеуі сызықтық болған жағдайда қарастырайық (формула).
a= =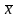
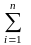хi ;
в= 
/
(
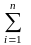
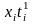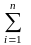)2 , (3)
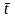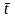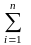мұндағы =ti- ; = ti;
Осындай жолмен келтіріп шығарылған теңдеу координат болсын t=0 нүктесінен t=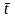 нүктесіне көшіруге сәйкес келеді.
Ең кіші квадраттар әдісін қолданып (2) теңдеудің коэфиценттерінің (а, b , с) мәндерін табайық (х=a+bt +ct2):
U=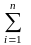 
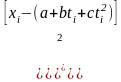, (4)
(4) – інші өрнек минимум мәнге ие болуы үшін оның барлық дербес туындылары нөлге иең болуы тиіс:
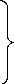
(5)
теңдеулер жүйесінен төмендегіні келтіріп шағарамыз:
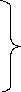
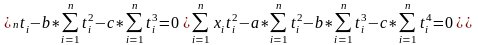(6)
=ti-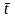 белгілеу ендіреміз, мұнда координат басы t= 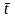нүктесіне көшеді. t1 айнымалысының тақ дәрежелілерінің қосындылары нөлге тең, яғни
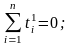
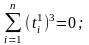
Осыны есепке алсақ, (6) теңдеулер жүйесі төмендегі көрініске келеді:
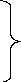
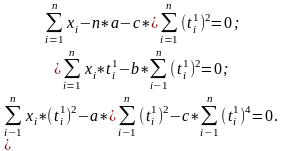(7)
(7)-нің екінші теңдеуінен
(8)
(7)-нің бірінші және үшінші теңдеулерінен
(9)
(10)
Нәтиже координат басының көшірілгендігін есепке алып тренд үшін екінші дәрежелі теңдеуді келтіріп шығарамыз:
(11).
Мысал. Дәріхана басқармасында кейбір дәрінің таралым шығыны 2-кестедегідей болсын. Теңдеулердің қайсы бірі уақыт қатары трендін адеквадратты түрде сипаттайды? Осы сұраққа жауап іздейік.
2-кесте
| Жыл | Шығын х, мың кг |
|
|
|
|
|
| 2005 | 6,2 | -4 | -24,8 | 16 | 99,2 | 256 |
| 2006 | 6,9 | -3 | -20,7 | 9 | 62,4 | 81 |
| 2007 | 7,4 | -2 | -14,8 | 4 | 29,6 | 16 |
| 2008 | 7,8 | -1 | -7,8 | 1 | 7,8 | 1 |
| 2009 | 14,3 | 0 | 0 | 0 | 0 | 0 |
| 2010 | 10,0 | 1 | 10,0 | 1 | 10 | 1 |
| 2011 | 14,1 | 2 | 28,2 | 4 | 56,3 | 16 |
| 2012 | 16,0 | 3 | 48,0 | 9 | 144 | 81 |
| 2013 | 18,1 | 4 | 72,4 | 16 | 289,6 | 256 |
|
| 100,8 | 0 | 90,5 | 60 | 698,7 | 708 |
Сызықтық теңдеу үшін
n=9;
-тің мәндерін есептейміз: =2005-2009= -4;
=2006-2009= -3; 
=2007-2009= -2; және т.с.с.
(Сызықтық, қисық сызықтық үшін бірдей)
Сызықтық және қисық сызықты теңдеулеріміз мынадай көріністе болады:
(12)
(13)
Сызықтық тренд үшін қалдық дисперсияны есептейміз:
3-кесте
| xi | 6,2 | 6,9 | 7,4 | 7,8 | 14,3 | 10,0 | 14,1 | 16,0 | 18,1 |
|
| 5,16 | 6,67 | 8,18 | 9,69 | 11,2 | 12,71 | 14,22 | 15,73 | 17,24 |
|
| 1,04 | 0,23 | -0,78 | -2,89 | 3,1 | -2,71 | -0,12 | 0,27 | 0,86 |
|
| 1,08 | 0,05 | 0,18 | 8,35 | 9,61 | 7,34 | 0,01 | 0,07 | 0,74 |
және т.с.с
Есептеулерді жалғастырып 2-кестені толтырып шығамыз.
кестеден
