Алгебра. 11 класс
Урок № 56
Дата:_____________
Учитель: Горбенко Алена Сергеевна
Тема: Логарифмические уравнения. Решение логарифмических уравнений
Тип урока: комбинированный
Цель урока: ознакомить учащихся с логарифмическими уравнениями и со способами их решения
Задачи:
Образовательные: повторить знания учащихся о логарифме числа, его свойствах; ввести понятие и определение логарифмического уравнения; сформировать алгоритм решения логарифмических уравнений; изучить способы решения логарифмических уравнений и закрепить их при выполнении упражнений; подготовка к ЕНТ;
Развивающие: развивать математическую грамотность и самостоятельность учащихся, умение пользоваться алгоритмом, развивать уметь анализировать и сравнивать;
Воспитательные: содействовать развитию мотиваций и самосовершенствования личности учащегося;
Оборудование: Школьные принадлежности, доска, мел, учебник, раздаточный материал.
Ход урока
Организационный момент
Взаимное приветствие;
Фиксация отсутствующих;
Объявление темы урока;
Постановка целей и задач урока учащимися.
Актуализация знаний
Устный опрос учащихся:
1. Дайте определение логарифма.
2. От любого ли числа можно найти логарифм?
3. Какое число может стоять в основании логарифма?
4. Функция y=log0,8 x является возрастающей или убывающей? Почему?
5. Какие значения может принимать логарифмическая функция?
6. Какие логарифмы называют десятичными, натуральными?
7. Назовите основные свойства логарифмов.
8. Можно ли перейти от одного основания логарифма к другому? Как это сделать?
Карточка №1: Вычислить: Карточка №2: Вычислить:
а) log64 + log69 =
б) log1/336 – log1/312 =
в) log211 - log 244=
г) log216 =
д) lоg3 √3=
е) log71 =
ж) log5 (1/625)=
з) log814 + log 832/7=
и) log35 ∙ log53=
к) 5 log5 49 =
л) 8 lоg 85 -1=
м) 25 –log 510=
а) log211 – log244 =
б) log1/64 + log1/69 =
в) log211 - log 244=
г) log216 =
д) lоg3 √3=
е) log71 =
ж) log5 (1/625) =
з) log814 + log 832/7=
и) log35 ∙ log53=
к) 5 log5 49 =
л) 8 lоg 85 -1=
м) 25 –log 510=
Изучение нового материала
Определение: Уравнение, содержащее переменную под знаком логарифма, называется логарифмическим. Простейшим примером логарифмического уравнения служит уравнение loga х =с (а 0, а≠ 1)
Способы решения логарифмических уравнений:
Решение уравнений на основании определения логарифма.
loga х = с (а 0, а≠ 1) имеет решение х = ас.
На основе определения логарифма решаются уравнения, в которых:
по данным основаниям и числу определяется логарифм,
по данному логарифму и основанию определяется число,
по данному числу и логарифму определяется основание.
Примеры:
log2 128= х, log16х = ¾, logх 27= 3,
2х= 128, х =16 ¾ , х3 =27,
2х = 27, х =2 3 , х3 = 33 ,
х =7 . х = 8. х =3.
С классом решить следующие уравнения:
а) log7(3х-1)=2 (ответ: х=3 1/3) б) log2(7-8х)=2 (ответ: х=3/8).
Метод потенцирования.
Под потенцированием понимается переход от равенства, содержащего логарифмы, к равенству, не содержащему их т.е.
loga f(х) = loga g(х), то f(х) = g(х), при условии, что f(х)0, g(х)0 , а 0, а≠ 1.
Пример: Решите уравнение
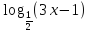 =
= 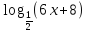
ОДЗ:
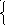
3х-10; х1/3
6х+80.
3х-1=6х+8
-3х=9, х=-3
-3 1/3 - неверно
Ответ: решений нет.
С классом решить следующее уравнение: lg(х2-2) = lg х (ответ: х=2)
Уравнения, решаемые с помощью применения основного логарифмического тождества.
Пример: Решите уравнение
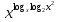 =log2(6-х)
=log2(6-х)ОДЗ:
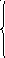 6-х0;
6-х0;х0;
х≠1;
log2х20;
х20.
Решение системы: (0;1)Ụ (1;6).
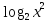 = log2(6-х)
= log2(6-х)х2 = 6-х
х2+х-6=0
х=-3 не принадлежит ОДЗ.
х=2 принадлежит ОДЗ.
Ответ: х=2
С классом решить следующее уравнение:
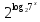 =
= 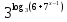 (ответ: х=1)
(ответ: х=1)
Метод приведения логарифмов к одному и тому же основанию.
Пример: Решите уравнение log16х+ log4х+ log2х=7
ОДЗ: х0
¼ log2х+½ log2х+ log2х=7
7/4 log2х=7
log2х=4
х=16 – принадлежит ОДЗ.
Ответ: х=16.
С классом решить следующее уравнение :
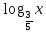 +
+ 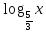 =3 (ответ: х=5/3)
=3 (ответ: х=5/3)
Уравнения, решаемые с помощью применения свойств логарифма.
Пример: Решите уравнение log2 (х +1) - log2 (х -2 ) = 2.
ОДЗ:
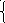
х+10;
х-20. х1.
Воспользуемся формулой преобразования разности логарифмов логарифм частного, получаем log2
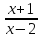 = 2, откуда следует
= 2, откуда следует 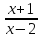 = 4.
= 4.Решив последнее уравнение, находим х = 3, 31 - верно
Ответ: х = 3.
С классом решить следующие уравнения:
а)log5 (х +1) + log5 (х +5) = 1 (ответ: х=0).
б)log9( 37-12х ) log7-2х 3 = 1,
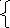
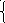
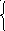
37-12х 0, х
7-2х 0, х
7-2х≠ 1; х≠ 3; х≠ 3;
log9( 37-12х ) / log3 (7-2х ) = 1,
½ log3( 37-12х ) = log3 (7-2х ) ,
log3( 37-12х ) = log3 (7-2х )2 ,
37-12х= 49 -28х +4х2 ,
4х2-16х +12 =0,
х2-4х +3 =0, Д=19, х1=1, х2=3, 3 –посторонний корень.
Ответ: х=1 корень уравнения.
в) lg(х2-6х+9) - 2lg(х - 7) = lg9.
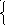
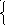
(х2-6х+9) 0, х≠ 3,
х-7 0; х 7; х 7.
lg ((х-3)/(х-7))2 = lg9
((х-3)/(х-7))2 = 9,
(х-3)/(х-7) = 3, (х-3)/(х-7)= - 3 ,
х- 3 = 3х -21 , х -3 =- 3х +21,
х =9. х=6 - посторонний корень.
Проверка показывает 9 корень уравнения.
Ответ: 9
Уравнения, решаемые введением новой переменной.
Пример: Решите уравнение lg2х - 6lgх+5 = 0.
ОДЗ: х0.
Пусть lgх = р, тогда р2-6р+5=0.
р1=1, р2=5.
Возвращаемся к замене:
lgх = 1, lgх =5
х=10, 100 – верно х=100000, 1000000 – верно
Ответ: 10, 100000
С классом решить следующее уравнение:
log62 х + log6 х +14 = (√16 – х2)2 +х2,
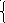
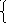
16 – х2 ≥0 ; - 4≤ х ≤ 4;
х 0 , х 0, О.Д.З. [ 0,4).
log62 х + log6 х +14 = 16 – х2 +х2,
log62 х + log6 х -2 = 0
заменим log6 х = t
t 2 + t -2 =0 ; D = 9 ; t1 =1 , t2 = -2.
log6 х = 1 , х = 6 посторонний корень .
log6 х = -2, х = 1/36 , проверка показывает 1/36 является корнем .
Ответ : 1/36.
Уравнения, решаемые с помощью разложения на множители.
Пример: Решите уравнение log4(2х-1)∙ log4х=2 log4(2х-1)
ОДЗ:
2х-10;
х 0. х½.
log4(2х-1)∙ log4х - 2 log4(2х-1)=0
log4(2х-1)∙(log4х-2)=0
log4(2х-1)=0 или log4х-2=0
2х-1=1 log4х = 2
х=1 х=16
1;16 – принадлежат ОДЗ
Ответ: 1;16
С классом решить следующее уравнение:
log3х ∙log3(3х-2)= log3(3х-2) (ответ: х=1)
Метод логарифмирования обеих частей уравнения.
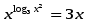 Пример:
Пример:Решите уравнения
Прологарифмируем обе части уравнения по основанию 3.
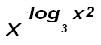
Получим log3 = log3 (3х)
получаем: log3 х2 log3 х = log3 (3х),
2log3 х log3 х = log3 3+ log3 х,
2 log32 х = log3 х +1,
2 log32 х - log3 х -1=0,
заменим log3 х = р , х 0
2 р 2 + р -2 =0 ; D = 9 ; р1 =1 , р2 = -1/2
log3 х = 1 , х=3,
log3 х = -1/ 2 , х= 1/√3.
Ответ: 3; 1/√3
С классом решить следующее уравнение:
log2 х - 1
х = 64 (ответ: х=8; х=1/4)
Функционально – графический метод.
Пример: Решите уравнения: log3 х = 12-х.
Так как функция у = log3 х возрастающая, а функция у =12-х убывающая на (0; + ∞) то заданное уравнение на этом интервале имеет один корень.
Построим в одной системе координат графики двух функций: у = log3 х и у =12-х.
При х=10 заданное уравнение обращается в верное числовое равенство 1=1. Ответ х=10.
С классом решить следующее уравнение:
1-√х =ln х (ответ: х=1).
Информация о домашнем задании:
Подведение итогов урока. Рефлексия
Карточка №1: Вычислить: Карточка №2: Вычислить:
а) log64 + log69 =
б) log1/336 – log1/312 =
в) log211 - log 244=
г) log216 =
д) lоg3 √3=
е) log71 =
ж) log5 (1/625)=
з) log814 + log 832/7=
и) log35 ∙ log53=
к) 5 log5 49 =
л) 8 lоg 85 -1=
м) 25 –log 510=
а) log211 – log244 =
б) log1/64 + log1/69 =
в) log211 - log 244=
г) log216 =
д) lоg3 √3=
е) log71 =
ж) log5 (1/625) =
з) log814 + log 832/7=
и) log35 ∙ log53=
к) 5 log5 49 =
л) 8 lоg 85 -1=
м) 25 –log 510=
Карточка №1: Вычислить: Карточка №2: Вычислить:
а) log64 + log69 =
б) log1/336 – log1/312 =
в) log211 - log 244=
г) log216 =
д) lоg3 √3=
е) log71 =
ж) log5 (1/625)=
з) log814 + log 832/7=
и) log35 ∙ log53=
к) 5 log5 49 =
л) 8 lоg 85 -1=
м) 25 –log 510=
а) log211 – log244 =
б) log1/64 + log1/69 =
в) log211 - log 244=
г) log216 =
д) lоg3 √3=
е) log71 =
ж) log5 (1/625) =
з) log814 + log 832/7=
и) log35 ∙ log53=
к) 5 log5 49 =
л) 8 lоg 85 -1=
м) 25 –log 510=
Карточка №1: Вычислить: Карточка №2: Вычислить:
а) log64 + log69 =
б) log1/336 – log1/312 =
в) log211 - log 244=
г) log216 =
д) lоg3 √3=
е) log71 =
ж) log5 (1/625)=
з) log814 + log 832/7=
и) log35 ∙ log53=
к) 5 log5 49 =
л) 8 lоg 85 -1=
м) 25 –log 510=
а) log211 – log244 =
б) log1/64 + log1/69 =
в) log211 - log 244=
г) log216 =
д) lоg3 √3=
е) log71 =
ж) log5 (1/625) =
з) log814 + log 832/7=
и) log35 ∙ log53=
к) 5 log5 49 =
л) 8 lоg 85 -1=
м) 25 –log 510=
Карточка №1: Вычислить: Карточка №2: Вычислить:
а) log64 + log69 =
б) log1/336 – log1/312 =
в) log211 - log 244=
г) log216 =
д) lоg3 √3=
е) log71 =
ж) log5 (1/625)=
з) log814 + log 832/7=
и) log35 ∙ log53=
к) 5 log5 49 =
л) 8 lоg 85 -1=
м) 25 –log 510=
а) log211 – log244 =
б) log1/64 + log1/69 =
в) log211 - log 244=
г) log216 =
д) lоg3 √3=
е) log71 =
ж) log5 (1/625) =
з) log814 + log 832/7=
и) log35 ∙ log53=
к) 5 log5 49 =
л) 8 lоg 85 -1=
м) 25 –log 510=

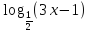 =
= 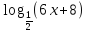
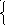
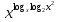 =
=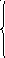 6-х0;
6-х0;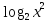 =
= 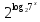 =
= 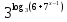 (ответ: х=1)
(ответ: х=1)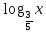 +
+ 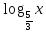 =3 (ответ: х=5/3)
=3 (ответ: х=5/3)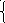
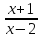 = 2, откуда следует
= 2, откуда следует 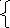
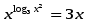 Пример:
Пример:



