19.02.2019г.
Открытый урок по математике.
Тема урока:
«Решение уравнений».
6 класс
Цели урока:
Образовательные:
Научить переносить слагаемые из одной части уравнения в другую и применять перенос слагаемых при решении уравнений;
Развивающие:
Развивать познавательные процессы, память, мышление, внимание, наблюдательность;
Воспитательные:
Способствовать выработке навыков самостоятельной работы.
Задачи урока:
1. Проверить усвоение материала по данной теме.
2. Закрепить навыки выполнения заданий по данной теме.
3. Формировать навыки самоконтроля в процессе выполнения заданий.
4. Формировать умение применять знания.
Образовательные результаты, которые буду достигнуты учащимися
1. Смотр знаний по свойствам с самопроверкой покажет знания учащихся способов решения уравнений , наличие адекватной самооценки деятельности.
2. Спланированное обобщение систематизирует знания, закрепит навыки выполнения заданий, способствует развитию математического мышления и речи.
3. Разнообразие форм работы на уроке способствует формированию умения применять знания в новой ситуации
Оборудование: доска, экран, проектор, компьютер.
Структура урока:
Оргмомент – 1мин.
Сообщение темы и целей урока – 2 мин.
Актуализация знаний – 7 мин.
Изучение нового материала – 10 мин.
Закрепление изученного материала – 20 мин.
Физкультминутка – 1мин, (внутри п.5.)
Домашнее задание – 1 мин,
Подведение итогов урока, рефлексия – 3 мин.
Ход урока.
Оргмомент.
Сообщение темы и целей урока, (слайд 2)
- Альберт Эйнштейн, один из основателей современной физики, сказал: «Мне приходится делить время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее. Политика существует только для данного момента, а уравнения (предлагается ученикам продолжить мысль учёного) будут существовать вечно».
Альберт Эйнштейн, один из основателей современной физики, сказал: «Мне приходится делить время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее. Политика существует только для данного момента, а уравнения (предлагается ученикам продолжить мысль учёного) будут существовать вечно».
Сегодня мы начинаем изучать тему «Решение уравнений». «Но мы уже учились решать уравнения!» -скажете вы. Учиться
Альберт Эйнштейн решать уравнения мы будем до окончания школы.
 Цель нашего урока: познакомиться с новыми правилами, позволяющими решать уравнения, учиться применять их при решении уравнений.
Цель нашего урока: познакомиться с новыми правилами, позволяющими решать уравнения, учиться применять их при решении уравнений.
И еще Французский писатель Анатоль Франц (1844-1924 гг.) заметил: «Что учиться можно только весело……..Чтоб ы переваривать знания, надо поглощать их с аппетитом»
Последуем совету писателя – будем на уроке активны, внимательны, будем «поглощать» знания с большим желанием, ведь они вам непременно пригодятся, а для начала давайте разогреемся и поработаем устно.
Актуализация опорных знаний.
Беседа: Давайте вспомним, что мы уж знаем. Но прежде – обратим внимание на карту самоконтроля.
| Задания | Результаты работы |
| 1. Устная работа (1 балл за каждый верный ответ) |
|
| 2. Работа в парах (2 балл за каждый верный ответ) |
|
| 3. Самостоятельная работа ( 4 или 5 баллов верный ответ) |
|
| 4. Дополнительные баллы (2 балла за каждый верный ответ) |
|
| Всего баллов: |
|
| Предварительная оценка: |
|
Что называется уравнением?
Что называется корнем уравнения?
Что значит « решить уравнение»?
Всегда ли уравнение имеет корни?
Как узнать, является ли данное число корнем уравнения?
Решите данные уравнения
2 х = - 2,6;
0 х = - 4;
– 12 х = 4;
– 13 х = 0;
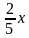 = 1;
= 1;
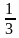 х = - 6;
х = - 6;
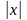 = 6.
= 6.
Изучение нового материала.
- Решите уравнения: а) х + 8 = - 15 ( х = - 23);
Но это уравнение можно решить по – другому – используя правило сложения противоположных чисел ( Сумма противоположных чисел равна нулю), т. е корни уравнения не изменятся, если прибавить или отнять от обеих частей уравнения числа противоположные числам в левой части уравнения – это правило № 1.
- Значит х + 8 = - 15,
х + 8 – 8 = - 15 – 8,
х = - 23.
- Слагаемые без переменной перешли из левой части уравнения в правую с противоположными знаками. Решим еще уравнение: 6 х – 2 = 3 х + 7.
Что нужно сделать, чтобы слагаемые с переменной были только в левой части, а слагаемые без переменной были в правой части? (Перенести их из одной части в другую с противоположными знаками)
6 х – 3 х = 7 + 2,
3х = 9,
х = 9 : 3,
х= 3.
Вывод: корни уравнения не изменятся, если слагаемые из одной части уравнения перенести в другую часть, изменив при этом его знак – это правило № 2.
Закрепление изученного материала.
Составить алгоритм решения уравнений: 2 (3x – 6) = 4 - 2x
| Шаг 1 | Раскрыть скобки, если это нужно сделать. | 6x – 12 = 4 - 2х |
| Шаг 2 | Все члены содержащие неизвестное переносим в левую часть, а известные в правую с противоположным знаком !! | 6х + 2х = 4 + 12 |
| Шаг 3 | Приводим подобные слагаемые. | 8 x = 16 |
| Шаг 4 | Делим обе части уравнения на коэффициент при неизвестном. | х = 16:8, х = 2 . |
|
| Не забудь написать ответ!!! | Ответ: 2. |
Решить уравнения: № 1316 (б) и 1342 (и) – фронтально; № 1316 (г) и 1342 (к) – работа в парах. (Использовать алгоритм)
Самостоятельная работа: вариант 1 (№1342(ж)); вариант 2 (№1342(з)) с последующей самопроверкой.
VI.Домашнее задание: 1) вопросы на стр. 230
2) № 1316 ( а, в), 1317 (а, в) , 1332, 1334.
VII. Подведение итогов:
Совместно с учащимися подводим итог урока о том, что узнали нового, чему
научились, насколько успешна была работа на уроке. Выставляются оценки за урок учащимся, принимавшим активное участие на уроке и тем, кто успешно справился с самостоятельной работой.
Рефлексия:
У каждого на парте лежат кружочки красного, желтого и зеленого цветов.
Уходя с урока ученики бросают в почтовый ящик круг определенного цвета:
зеленый – все понял и научился применять формулы;
желтый – понял, но затрудняюсь применять;
красный – ничего не понял, нуждаюсь в дополнительной консультации.

 = 1;
= 1; х = - 6;
х = - 6;  = 6.
= 6. Альберт Эйнштейн, один из основателей современной физики, сказал: «Мне приходится делить время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее. Политика существует только для данного момента, а уравнения (предлагается ученикам продолжить мысль учёного) будут существовать вечно».
Альберт Эйнштейн, один из основателей современной физики, сказал: «Мне приходится делить время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее. Политика существует только для данного момента, а уравнения (предлагается ученикам продолжить мысль учёного) будут существовать вечно».
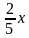 = 1;
= 1;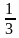 х = - 6;
х = - 6; 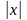 = 6.
= 6.












