КИМ по информатике

Министерство образования Ставропольского края

Государственное бюджетное профессиональное образовательное учреждение «Государственный агротехнический колледж» с. Московское

РАССМОТРЕНО и ОДОБРЕНО		УТВЕРЖДАЮ
на заседании П(Ц)К ООД, ЕН и ОГСЭ		Заместитель директора по УР
Протокол №_____ от ____________		___________Л.С. Набокова
Руководитель________ А.С. Сопова		«___»____________20___ г.

КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫЕ МАТЕРИАЛЫ

для текущего контроля успеваемости и промежуточной аттестации

по учебной дисциплине общеобразовательного цикла ОУД.04 Математика

Индекс, наименование учебной дисциплины

по профессии 43.01.09 Повар, кондитер

код, наименование специальности

Вид промежуточной аттестации: экзамен

Учебный год 2021-2024 семестр 1-6

Курс 1,2,3 группы № 101,102,201,202,301,302

Разработчик: Сопова Антонина Сергеевна

Ф.И.О. преподавателя

СОДЕРЖАНИЕ

1. Паспорт комплекта контрольно-измерительных материалов …………………………………4

2. Формы контроля и оценки освоения учебной дисциплины по темам (разделам)…….. …….10

3. Контрольно-измерительные материалы для проведения текущего контроля ………………..

4. Контрольно-измерительные материалы для контроля по разделу (рубежный контроль)……

5. Контрольно-измерительные материалы для контроля выполнения

индивидуального проекта…………………………………………………………………………...

6 Контрольно-измерительные материалы для промежуточной аттестации…………………… .

1. ПАСПОРТ КОМПЛЕКТА КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫХ МАТЕРИАЛОВ

1.1. Область применения контрольно-измерительных материалов (далее – КИМ) КИМ учебной дисциплины ОУД.04 Математика является частью основной образовательной программы в соответствии с ФГОС СПО 43.01.09 Повар, кондитер.

КИМ предназначены для оценки достижений запланированных результатов по учебной дисциплине в процессе текущего и рубежного контроля, промежуточной аттестации.

1.2. Цель и планируемые результаты освоения дисциплины:

Содержание программы учебной дисциплины ОУД.04 Математика направлено на достижение следующих целей:

- формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;

- развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, для продолжения образования и самообразования;

- овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения смежных естественнонаучных дисциплин на базовом уровне и дисциплин профессионального цикла, для получения образования в областях, не требующих углубленной математической подготовки;

- воспитание средствами математики культуры личности, понимания значимости математики для научно- технического прогресса, отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей.

Освоение содержания учебной дисциплины ОУД.04 Математика обеспечивает достижение студентами следующих результатов:

• личностных:

− Л1: сформированность представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, идеях и методах математики;

− Л2: понимание значимости математики для научно-технического прогресса, сформированность отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей;

− Л3: развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, для продолжения образования и самообразования;

− Л4: овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для освоения смежных естественно-научных дисциплин и дисциплин профессионального цикла, для получения образования в областях, не требующих углубленной математической подготовки;

− Л5: готовность и способность к образованию, в том числе самообразованию, на протяжении всей жизни; сознательное отношение к непрерывному образованию как условию успешной профессиональной и общественной деятельности;

− Л6: готовность и способность к самостоятельной творческой и ответственной деятельности;

− Л7: готовность к коллективной работе, сотрудничеству со сверстниками в образовательной, общественно полезной, учебно-исследовательской, проектной и других видах деятельности;

− Л8: отношение к профессиональной деятельности как возможности участия в решении личных, общественных, государственных, общенациональных проблем;

• метапредметных:

− М1: умение самостоятельно определять цели деятельности и составлять планы деятельности; самостоятельно осуществлять, контролировать и корректировать деятельность; использовать все возможные ресурсы для достижения поставленных целей и реализации планов деятельности; выбирать успешные стратегии в различных ситуациях;

− М2: умение продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции других участников деятельности, эффективно разрешать конфликты;

− М3: владение навыками познавательной, учебно-исследовательской и проектной деятельности, навыками разрешения проблем; способность и готовность к самостоятельному поиску методов решения практических задач, применению различных методов познания;

− М4: готовность и способность к самостоятельной информационно-познавательной деятельности, включая умение ориентироваться в различных источниках информации, критически оценивать и интерпретировать информацию, получаемую из различных источников;

− М5: владение языковыми средствами: умение ясно, логично и точно излагать свою точку зрения, использовать адекватные языковые средства;

− М6: владение навыками познавательной рефлексии как осознания совершаемых действий и мыслительных процессов, их результатов и оснований, границ своего знания и незнания, новых познавательных задач и средств для их достижения;

− М7: целеустремленность в поисках и принятии решений, сообразительность и интуиция, развитость пространственных представлений; способность воспринимать красоту и гармонию мира;

• предметных:

− П1: сформированность представлений о математике как части мировой культуры и месте математики в современной цивилизации, способах описания явлений реального мира на математическом языке;

− П2: сформированность представлений о математических понятиях как важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления; понимание возможности аксиоматического построения математических теорий;

− П3: владение методами доказательств и алгоритмов решения, умение их применять, проводить доказательные рассуждения в ходе решения задач;

− П4: владение стандартными приемами решения рациональных и иррациональных, показательных, степенных, тригонометрических уравнений и неравенств, их систем; использование готовых компьютерных программ, в том числе для поиска пути решения и иллюстрации решения уравнений и неравенств;

− П5: сформированность представлений об основных понятиях математического анализа и их свойствах, владение умением характеризовать поведение функций, использование полученных знаний для описания и анализа реальных зависимостей;

− П6: владение основными понятиями о плоских и пространственных геометрических фигурах, их основных свойствах; сформированность умения распознавать геометрические фигуры на чертежах, моделях и в реальном мире; применение изученных свойств геометрических фигур и формул для решения геометрических задач и задач с практическим содержанием;

− П7: сформированность представлений о процессах и явлениях, имеющих вероятностный характер, статистических закономерностях в реальном мире, основных понятиях элементарной теории вероятностей; умений находить и оценивать вероятности наступления событий в простейших практических ситуациях и основные характеристики случайных величин;

− П8: владение навыками использования готовых компьютерных программ при решении задач.

Контроль и оценка результатов освоения учебной дисциплины

Результаты обучения	Критерии оценки	Методы оценки
Личностные: Л1: сформированность представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, идеях и методах математики; Л2: понимание значимости математики для научно-технического прогресса, сформированность отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей; Л3: развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, для продолжения образования и самообразования; Л4: овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для освоения смежных естественно-научных дисциплин и дисциплин профессионального цикла, для получения образования в областях, не требующих углубленной математической подготовки; Л5: готовность и способность к образованию, в том числе самообразованию, на протяжении всей жизни; сознательное отношение к непрерывному образованию как условию успешной профессиональной и общественной деятельности; Л6: готовность и способность к самостоятельной творческой и ответственной деятельности; Л7: готовность к коллективной работе, сотрудничеству со сверстниками в образовательной, общественно полезной, учебно-исследовательской, проектной и других видах деятельности; Л8: отношение к профессиональной деятельности как возможности участия в решении личных, общественных, государственных, общенациональных проблем	Представляет математику как средство моделирования явлений и процессов. Понимает значимость математики для научно-технического прогресса, формирует отношение к математике как к части общечеловеческой культуры Развивает логическое мышление, пространственное воображение на уровне, необходимом для будущей профессиональной деятельности Овладевает математическими знаниями и умениями Формирует готовность и способность к образованию и самообразованию Формирует готовность и способность к самостоятельной творческой деятельности Формирует готовность к коллективной работе Формирует отношение к профессиональной деятельности как возможности участия в решении личных, общественных, государственных, общенациональных проблем	Устный опрос Устный опрос Практические работы Практические работы Практические работы Контрольные работы Практические работы Практические работы Тестирование
Метапредметные: М1: умение самостоятельно определять цели деятельности и составлять планы деятельности; самостоятельно осуществлять, контролировать и корректировать деятельность; использовать все возможные ресурсы для достижения поставленных целей и реализации планов деятельности; выбирать успешные стратегии в различных ситуациях; М2: умение продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции других участников деятельности, эффективно разрешать конфликты; М3: владение навыками познавательной, учебно-исследовательской и проектной деятельности, навыками разрешения проблем; способность и готовность к самостоятельному поиску методов решения практических задач, применению различных методов познания; М4: готовность и способность к самостоятельной информационно-познавательной деятельности, включая умение ориентироваться в различных источниках информации, критически оценивать и интерпретировать информацию, получаемую из различных источников; М5: владение языковыми средствами: умение ясно, логично и точно излагать свою точку зрения, использовать адекватные языковые средства; М6: владение навыками познавательной рефлексии как осознания совершаемых действий и мыслительных процессов, их результатов и оснований, границ своего знания и незнания, новых познавательных задач и средств для их достижения; М7:целеустремленность в поисках и принятии решений, сообразительность и интуиция, развитость пространственных представлений; способность воспринимать красоту и гармонию мира	Определяет самостоятельно цели деятельности и составляет планы деятельности Осуществляет, контролирует и корректирует деятельность Использует все возможные ресурсы для достижения поставленных целей и реализации планов деятельности Выбирает успешные стратегии в различных ситуациях Умеет продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции других участников деятельности, эффективно разрешать конфликты Владеет навыками познавательной, учебно-исследовательской и проектной деятельности, навыками разрешения проблем Готов к самостоятельному поиску методов решения практических задач, применению различных методов познания Ориентируется в различных источниках информации Критически оценивает и интерпретирует информацию, получаемую из различных источников Умеет ясно, логично и точно излагать свою точку зрения, использует адекватные языковые средства Владеет навыками познавательной рефлексии как осознания совершаемых действий и мыслительных процессов, их результатов и оснований, границ своего знания и незнания, новых познавательных задач и средств для их достижения Принимает решения, развивает пространственные представления	Практические работы Практические работы Контрольные работы Практические работы Практические работы Практические работы Практические работы Контрольные работы Тестирование Практические работы Практические работы
Предметные: П1: сформированность представлений о математике как части мировой культуры и месте математики в современной цивилизации, способах описания явлений реального мира на математическом языке; П2: сформированность представлений о математических понятиях как важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления; понимание возможности аксиоматического построения математических теорий; П3: владение методами доказательств и алгоритмов решения, умение их применять, проводить доказательные рассуждения в ходе решения задач; П4: владение стандартными приемами решения рациональных и иррациональных, показательных, степенных, тригонометрических уравнений и неравенств, их систем; использование готовых компьютерных программ, в том числе для поиска пути решения и иллюстрации решения уравнений и неравенств; П5: сформированность представлений об основных понятиях математического анализа и их свойствах, владение умением характеризовать поведение функций, использование полученных знаний для описания и анализа реальных зависимостей; П6: владение основными понятиями о плоских и пространственных геометрических фигурах, их основных свойствах; сформированность умения распознавать геометрические фигуры на чертежах, моделях и в реальном мире; применение изученных свойств геометрических фигур и формул для решения геометрических задач и задач с практическим содержанием; П7: сформированность представлений о процессах и явлениях, имеющих вероятностный характер, статистических закономерностях в реальном мире, основных понятиях элементарной теории вероятностей; умений находить и оценивать вероятности наступления событий в простейших практических ситуациях и основные характеристики случайных величин; П8: владение навыками использования готовых компьютерных программ при решении задач.	Описывает явления реального мира на математическом языке Формирует представления о математических понятиях как важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления Понимает возможности аксиоматического построения математических теорий Владеет методами доказательств и алгоритмов решения Применяет методы доказательств и алгоритмов решения Проводит доказательные рассуждения в ходе решения задач Владеет стандартными приемами решения рациональных и иррациональных, показательных, степенных, тригонометрических уравнений и неравенств, их систем Формирует представления об основных понятиях математического анализа и их свойствах Характеризует поведение функций Применяет полученные знания для описания и анализа реальных зависимостей Владеет основными понятиями о плоских и пространственных геометрических фигурах, их основных свойствах Распознает геометрические фигуры на чертежах, моделях и в реальном мире Решает геометрические задачи с практическим содержанием Формирует представления о процессах и явлениях, имеющих вероятностный характер, статистических закономерностях в реальном мире, основных понятиях элементарной теории вероятностей Находит и оценивает вероятности наступления событий в простейших практических ситуациях и основные характеристики случайных величин Использует готовые компьютерные программы при решении задач	Тестирование Устный опрос Тестирование Практические работы Практические работы Практические работы Практические работы Контрольные работы Практические работы Тестирование Тестирование Практические работы Тестирование Практические работы Контрольные работы Тестирование Практические работы Практические работы

2. ФОРМЫ КОНТРОЛЯ И ОЦЕНКИ ОСВОЕНИЯ УЧЕБНОЙ ДИСЦИПЛИНЫ ПО

ТЕМАМ (РАЗДЕЛАМ)

Элемент учебной дисциплины	Формы и методы контроля
	Текущий контроль			Рубежный контроль (Контроль по разделу)			Промежуточная аттестация
	Формы контроля	Осваиваемые результаты	Формы контроля		Осваиваемые результаты	Формы контроля			Осваиваемые результаты
Раздел 1. Алгебра
Тема 1.1 Развитие понятия о числе.	ПЗ № 1 ПЗ № 2 ПЗ № 3 ПЗ № 4	Л1,Л2,Л3,Л4,Л5 М1,М2, М4 П1, П2
Тема 1.2.Функции, их свойства и графики	ПЗ № 5 ПЗ № 6 ПЗ № 7	Л1,Л2,Л3,Л4,Л5 М1,М2, М4 П1, П2
Тема 1.3. Корни, степени и лога-рифмы.	ПЗ № 8 ПЗ № 9 ПЗ № 10 ПЗ № 11 ПЗ № 12 ПЗ № 13 ПЗ № 14 ПЗ № 15 ПЗ № 16	Л1,Л2,Л3,Л4,Л5 М1,М2, М4 П1, П2
Тема 1.4. Основы тригонометрии.	ПЗ № 17 ПЗ № 18 ПЗ № 19 ПЗ № 20	Л1,Л2,Л3,Л4,Л5 М1,М2, М4 П1, П2
Контроль по разделу 1.			Контроль ная работа №1 - №3		Л1,Л2,Л3,Л4, Л5 М1,М2,М3, М4 П1, П2,П4
Раздел 2. Начала математического анализа
Тема 2.1. Последовательности	ПЗ № 21	Л1,Л2,Л3,Л4,Л5 М1, М2, М3 П5
Тема 2.2. Основы дифференциального исчисления.	ПЗ № 22 ПЗ № 23 ПЗ № 24 ПЗ № 25 ПЗ № 26 ПЗ № 27	Л1,Л2,Л3,Л4,Л5 М1, М2, М3 П5
Тема 2.3. Основы интегрального исчисления.	ПЗ № 28 ПЗ № 29 ПЗ № 30 ПЗ № 31
Контроль по разделу 2			Контроль ная работа №4		Л1,Л2,Л3,Л4, Л5 М1,М2,М3 П5
Раздел 3. Комбинаторика, статистика и теория вероятностей
Тема 3.1. Элементы комбинаторики.	ПЗ № 32	Л1,Л2,Л3,Л4,Л5 М3,М6,М7 П1,П2,П7
Тема 3.2. Элементы теории вероятностей.	ПЗ № 33 Тест № 1	Л1,Л2,Л3,Л4,Л5 М3,М6,М7 П1,П2,П7
Тема 3.3. Элементы математической статистики.	ПЗ № 34	Л1,Л2,Л3,Л4,Л5 М3,М6,М7 П1,П2,П7
Раздел 4. Геометрия
Тема 4.1. Прямые и плоскости в пространстве.	ПЗ № 35 ПЗ № 36 Тест № 2	Л1,Л2,Л3,Л4,Л5 М3,М4,М5, М6 П3,П6,П8
Тема 4.2. Многогранники.	ПЗ № 37 ПЗ № 38 ПЗ № 39 ПЗ № 40	Л1,Л2,Л3,Л4,Л5 М3,М4,М5, М6 П3,П6,П8
Тема 4.3. Тела и поверхности вращения.	ПЗ № 41 ПЗ № 42 ПЗ № 43	Л1,Л2,Л3,Л4,Л5 М3,М4,М5, М6 П3,П6,П8
Тема 4.4. Измерения в геометрии.	ПЗ № 44 ПЗ № 45 ПЗ № 46 ПЗ № 47 ПЗ № 48	Л1,Л2,Л3,Л4,Л5 М3,М4,М5, М6 П3,П6,П8
Тема 4.5. Координаты и векторы.	ПЗ № 49 ПЗ № 50	Л1,Л2,Л3,Л4,Л5 М3,М4,М5, М6 П3,П6,П8
Контроль по разделу 4			Итоговая контроль ная работа		Л5 Л6 М3 М4 М5 П3 П6 П8
Промежуточная аттестация						экзамен		Л1,Л2,Л3,Л4, Л5,Л6,Л7,Л8 М1,М2,М3,М4, М5,М6,М7 П1,П2,П3,П4, П5,П6,П7,П8

3. КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫЕ МАТЕРИАЛЫ ДЛЯ ПРОВЕДЕНИЯ

ТЕКУЩЕГО КОНТРОЛЯ

УСТНЫЙ ОПРОС ОБУЧАЮЩИХСЯ

Устный опрос № 1

Вопросы для устного опроса №1

1.Что изучает наука математика?

2.Какие основные понятия математики вы знаете?

3.Какова значимость математики для научно-технического прогресса?

4.Назовите основные математические понятия как важнейшие математические модели, позволяющие описывать и изучать разные процессы и явления

Критерии оценивания устного ответа:

Ответ оценивается отметкой «5», если обучающийся:

• полно раскрыл содержание материала в объеме, предусмотрен­ном программой и учебником,

• изложил материал грамотным языком в определенной логиче­ской последовательности, точно используя математическую термино­логию и символику;

• правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

• показал умение иллюстрировать теоретические положения конк­ретными примерами, применять их в новой ситуации при выполне­нии практического задания;

• продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость используемых при от­работке умений и навыков;

• отвечал самостоятельно без наводящих вопросов преподавателя. Возможны одна - две неточности при освещении второстепенных вопросов или в выкладках, которые обучающийся легко исправил по за­мечанию преподавателя.

Ответ оценивается отметкой «4», если он удовлетворяет в основ­ном требованиям на оценку «5», но при этом имеет один из недо­статков:

• в изложении допущены небольшие пробелы, не исказившие ма­тематическое содержание ответа;

• допущены один – два недочета при освещении основного содержа­ния ответа, исправленные по замечанию преподавателя;

• допущены ошибка или более двух недочетов при освещении вто­ростепенных вопросов или в выкладках, легко исправленные по замечанию преподавателя.

Отметка «3» ставится в следующих случаях:

• неполно или непоследовательно раскрыто содержание материа­ла, но показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программного ма­териала (определенные «Требованиями к математической подготов­ке учащихся»);

• имелись затруднения или допущены ошибки в определении поня­тий, использовании математической терминологии, чертежах, вы­кладках, исправленные после нескольких наводящих вопросов преподавателя;

• обучающийся не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обя­зательного уровня сложности по данной теме;

• при знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.

Отметка «2» ставится в следующих случаях:

• не раскрыто основное содержание учебного материала;

• обнаружено незнание или непонимание обучающимся большей или наиболее важной части учебного материала;

• допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов преподавателя.

• Отметка «1» ставится, если: обучающийся обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из по­ставленных вопросов по изучаемому материалу.

ТЕСТОВЫЕ ЗАДАНИЯ

Тест № 1

Тестовое задание для текущего контроля знаний

М 1. Перпендикуляром к плоскости α является

отрезок

1) АМ 2) АВ 3) МО 4) ОВ

2. Наклонной к плоскости α является отрезок

1) ОВ 2) МВ 3) АО 4) МО

О α 3. Проекцией наклонной АМ на плоскость α

является отрезок 1)ОВ 2) АВ 3) МВ 4) АО

А В 4. Расстояние между основаниями наклонных

1. АВ 2) АО 3) ОВ 4) ОМ

5. Угол между наклонной МВ и плоскостью α

1)

6. Найти длину проекции наклонной к плоскости, если длина перпендикуляра 4 см, длина наклонной 5 см.

7. Найти длину наклонной, если расстояние от т.А до плоскости α равно 6см, угол между наклонной и плоскостью – 30⁰.

8. Из точки К проведены к плоскости перпендикуляр КО и наклонные КА и КВ. Длины наклонных соответственно равны 13 см и 20 см. Проекция наклонной АК равна 5 см. Найти проекцию наклонной КВ.

9. Через точку пересечения диагоналей ромба АВСD проведен к его плоскости перпендикуляр МО, равный 12 см. Диагонали ромба равны 18 см и 10 см.

Найдите: 1) длины наклонных МА, МВ, МС и МD;

2)расстояние между основаниями этих наклонных.

Тест № 2

Тестовое задание для текущего контроля знаний

Вариант 1

1. К каждому многограннику укажите букву соответствующего изображения многогранника с рисунка 1:

- невыпуклый многогранник ……..

- параллелепипед ………………….

- наклонная призма ………………..

- прямая призма ………………..….

- пирамида ……………………..…..

- усечённая пирамида ……………..

- правильный октаэдр ……………..

- правильный тетраэдр …………….

- правильный икосаэдр …………….

- куб …………………………………

- правильный додекаэдр …………….

А Б В Г

Д Е Ж З

И К Л М рис.1

1. Какие из утверждений справедливы для правильной пирамиды:

- в её основании лежит правильный многоугольник;

ДА НЕТ

- все её грани правильные многоугольники;

ДА НЕТ

- АПОФЕМОЙ называется высота правильной пирамиды;

ДА НЕТ

- отрезок, соединяющий вершину пирамиды с центром основания, является её высотой;

ДА НЕТ

- все боковые грани правильной пирамиды равны;

ДА НЕТ

- основанием правильной пирамиды может быть квадрат;

ДА НЕТ

- основанием правильной пирамиды может быть трапеция;

ДА НЕТ

1. Изображённый на рисунке 2 многогранник называется…………………

…………………………………… Назовите его элементы

4. На рисунке 3 изображена …………………………………………………

…………………………………… Запишите, как называются перечисленные элементы вашего многогранника

1. О каких многогранниках идёт речь в приведённых ниже теоремах (впишите их названия вместо точек):

Теорема 1. Площадь боковой поверхности ………………………………………

………………………………………………. равна произведению полусуммы периметров основания на апофему.

Теорема 2. Площадь боковой поверхности ………………………………………..

равна произведению периметра основания на высоту ……………………………

Теорема 3. Площадь боковой поверхности ………………………………………..

равна половине произведения периметра основания на апофему.

Вариант 2

1. К каждому многограннику укажите букву соответствующего изображения многогранника с рисунка 1:

- невыпуклый многогранник ……..

- параллелепипед ………………….

- наклонная призма ………………..

- прямая призма ………………..….

- пирамида ……………………..…..

- усечённая пирамида ……………..

- правильный октаэдр ……………..

- правильный тетраэдр …………….

- правильный икосаэдр …………….

- куб …………………………………

- правильный додекаэдр …………….

А Б В Г

Д Е Ж З

И К Л М рис.1

1. Какие из утверждений справедливы для правильной пирамиды:

- в её основании может лежать любой многоугольник;

ДА НЕТ

- все её боковые грани равнобедренные треугольники;

ДА НЕТ

- высота её боковой грани, проведённая из вершины, называется АПОФЕМОЙ;

ДА НЕТ

- высота правильной пирамиды не всегда совпадает с центром основания;

ДА НЕТ

- все ребра правильной пирамиды равны;

ДА НЕТ

- основанием правильной пирамиды может быть ромб;

ДА НЕТ

- основанием правильной пирамиды может быть равносторонний треугольник;

ДА НЕТ

1. Изображённый на рисунке 2 многогранник называется…………………

…………………………………… Назовите его элементы

4. На рисунке 3 изображена …………………………………………………

…………………………………… Запишите, как называются перечисленные элементы вашего многогранника

5.О каких многогранниках идёт речь в приведённых ниже теоремах (впишите их названия вместо точек):

Теорема 1. Площадь боковой поверхности ………………………………………

………………………………………………. равна произведению полусуммы периметров основания на апофему.

Теорема 2. Площадь боковой поверхности ………………………………………..

равна произведению периметра основания на высоту ……………………………

Теорема 3. Площадь боковой поверхности ………………………………………..

равна половине произведения периметра основания на апофему.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ (РАБОТА)

Список практических занятий:

ПЗ № 1. Выполнение действий с натуральными числами, дробями.

ПЗ № 2. Решение уравнений и неравенств.

ПЗ № 3. Решение задач на проценты и пропорции.

ПЗ № 4. Вычисление площадей фигур.

ПЗ № 5. Исследование функции.

ПЗ № 6. Построение графиков функций.

ПЗ № 7. Преобразование функций.

ПЗ № 8. Вычисление степеней с целыми показателями.

ПЗ № 9. Вычисление корней.

ПЗ № 10. Решение иррациональных уравнений.

ПЗ № 11. Вычисление степеней с рациональным показателем.

ПЗ № 12. Решение показательных уравнений.

ПЗ № 13. Решение показательных неравенств.

ПЗ № 14. Вычисление логарифмов.

ПЗ № 15. Решение логарифмических уравнений.

ПЗ № 16. Решение логарифмических неравенств.

ПЗ № 17. Преобразование тригонометрических уравнений.

ПЗ № 18. Применение основных формул тригонометрии.

ПЗ № 19. Вычисление значений тригонометрических функций.

ПЗ № 20. Решение тригонометрических уравнений.

ПЗ № 21. Вычисление пределов числовых последовательностей.

ПЗ № 22. Применение правил нахождения производных.

ПЗ № 23. Вычисление производных суммы и разности.

ПЗ № 24. Вычисление производных произведения и частного.

ПЗ № 25. Применение производной к исследованию функций.

ПЗ № 26. Исследование функции на экстремум.

ПЗ № 27. Нахождение наибольшего и наименьшего значений функции.

ПЗ № 28. Применение основных методов интегрирования.

ПЗ № 29. Вычисление площади криволинейной трапеции.

ПЗ № 30. Применение формулы Ньютона-Лейбница.

ПЗ № 31. Вычисление площадей криволинейных фигур.

ПЗ № 32. Применение правил комбинаторики.

ПЗ № 33. Нахождение числовых характеристик дискретной величины.

ПЗ № 34. Вычисление моды, медианы и среднего арифметического.

ПЗ № 35.Определение взаимного расположения прямых и плоскостей.

ПЗ № 36. Решение задач.

ПЗ № 37. Решение задач.

ПЗ № 38. Построение сечений многогранников.

ПЗ № 39. Изготовление моделей многогранников.

ПЗ № 40. Решение задач.

ПЗ № 41. Решение задач.

ПЗ № 42. Построение сечений тел вращения.

ПЗ № 43. Решение задач.

ПЗ № 44.Вычисление площадей поверхностей многогранников.

ПЗ № 45. Вычисление площадей поверхностей тел вращения.

ПЗ № 46. Решение задач.

ПЗ № 47. Вычисление объемов многогранников и тел вращения

ПЗ № 48. Решение задач.

ПЗ № 49. Прямоугольная система координат в пространстве.

ПЗ № 50. Действия с векторами.

ПЗ№73.Вычисление скалярного произведения векторов.

Содержание, этапы проведения и критерии оценивания практических работ представлены в методических указаниях по проведению практических работ.

4. КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫЕ МАТЕРИАЛЫ ДЛЯ КОНТРОЛЯ ПО РАЗДЕЛУ

(РУБЕЖНЫЙ КОНТРОЛЬ)

Контрольная работа № 1

Время выполнения: 45мин

Условия выполнения (используемые справочники, таблицы, наличие раздаточного материала): нет

Вариант – 1

1. Вычислите:

а) 205 – 0,45(0,5 + 155,4 : 14,8) =

б) (6 7/12 – 3 17/36) • ½ - 4 1/3 : 13/20=

1. Решите уравнение:

а) 2(4 – 9х) – (2х + 3) = - 8(4 – х) + 3(1 + 2х)

б) х² – 10х + 21=0

1. Решите неравенство:

а) 3(2х – 1) 2(х + 2) + х + 5

б) 2(3 – 2х) + 3(2 – х) ≤ 40

1. В равнобедренном треугольнике боковая сторона равна 20см, а угол, лежащий напротив основания равен 60⁰. Найти площадь треугольника.

2. На прошлогоднем экзамене по математике 140 старшеклассников получили пятерки. В этом году число отличников выросло на 15%. Сколько человек получили пятерки за экзамен по математике в этом году?

   

3. Год назад школу закончили 100 ребят. А в это году выпускников на 25% меньше. Сколько выпускников в этом году?

4. Решить систему уравнений: х + 5у = 6,

2х + 3у =5.

Вариант – 2

1. Вычислите:

а) 322,84 : 1,4 + 7,03 – 24,5 • 1,2 =

б) 2 ½ • 48 – 3 2/3 : 1/18 + 5 5/12 : 7/36 =

2. Решите уравнение:

а) 8(4 – 3у) – (7 – 2у)= - (6 + 3у) + 8(у – 2)

б) х² + 3х – 4 =0

3. Решите неравенство:

а) 10х + 9 -3(2 – 5х)

б) 2(х – 7) – 3(х – 2) ≤ 6(1 + х)

4. Проезд на автобусе стоит 20 рублей. В дни школьных каникул для учащихся ввели скидку 25%. Сколько стоит проезд на автобусе в дни школьных каникул?

5. У яхты два паруса: грот и стаксель. Оба паруса имеют форму прямоугольного треугольника. У грота катеты имеют длину 3 м и 5 м. У стакселя катеты имеют длину 1,5 м и 4 м. Сколько квадратных метров парусины требуется для изготовления этих парусов?

6. В школьной библиотеке 5780 учебников, что составляет 85% всех книг, имеющихся в библиотеке. Сколько всего книг в школьной библиотеке?

7.Решить систему уравнений: х – 2у = -7,

4х + 5у = 11.

Варианты правильных ответов

Критерии оценивания контрольной работы

Контрольная работа № 2.

Время выполнения: 90мин

Условия выполнения (используемые справочники, таблицы, наличие раздаточного материала): нет

Вариант 1

1. Вынесите множитель за знак корня:

А) ⁷√4b;

Б) ³√2²a⁴;

В) ⁶√64a⁸b¹¹;

Г) ³√54а¹⁰

1. Вычислите:

А) 3^0,5log₃ ⁴

Б) 81^-0,75 + (1/125)^-1/3 – (1/32)^-3/5

В) (27^2/5·2^1/5·2)^5/6

Г) (4³√-4)³

1. Упростите:

А) a^3/4 b^5/24 : (a^5/12 b^-1/8)

Б) a^5/6 b^7/12 a^-3/4 b^-2/3

В) (a^√5)^√5

1. Внесите множитель под знак корня:

А) 2b^2/3;

Б) (4ab)^5/7;

В) (32a)^-3/4;

Г) 16^5/4

1. Найдите значение функции f(x)=5x² – 3x + 4 в точках х=-2;3;5

2. Постройте в одной системе координат графики функций у=3х², у=5х-2.

3. Решите уравнения:

А) 0,01х² – 10 =0

Б) х⁶ – 64=0

Вариант 2

1. Вынесите множитель за знак корня:

А) ⁷√5a;

Б) ³√4²b⁴;

В) ⁴√6a¹²b⁶;

Г) ⁵√128а⁷

1. Вычислите:

А) ₇^-2log₇ ⁵

Б) 0,001^-1/3 – 2^-2 ·64^2/3 – 8^-4/3 + (9⁰)²

В) (72^2/3)^1/2·36^1/6 : 2^4/3

Г) (3⁵√-3)⁵

1. Упростите:

А) a^-9/2 b^1/12 : (a^-19/4 b^1/3)

Б) a^1/3 b^5/3 a^1/6 b^-1/6

В) (b^√3)^√3

1. Внесите множитель под знак корня:

А) 2b^2/3;

Б) (4ab)^5/7;

В) (32a)^-3/4;

Г)16^5/4

1. Найдите значение функции f(x)=4x² + 4x - 4 в точках х=-3;2;6

2. Постройте в одной системе координат графики функций у= - 2х², у=3х+5.

3. Решите уравнения:

А) 0,02х⁶ – 1,28=0

Б) х⁵ – 243=0

Контрольная работа № 3.

Время выполнения: 90мин

Условия выполнения (используемые справочники, таблицы, наличие раздаточного материала): нет

Вариант – 1

1. Выразить в радианной мере величины углов:

а) 35⁰; б) 112⁰; в) 270⁰; г) 320⁰

1. Выразить в градусной мере величины углов:

а) π/4; б) 11π/6; в) 5π/12; г) 3π/5

1. Вычислить:

а) 2sin 5π/4 + 2cos 3π/4 – 3ctg² 5π/6=

б) 6sin π/6 – 2cos0 + 2tg²π/3=

1. Решить уравнения:

а) sin2x=√2/2

б) 2cos(x/2 –π/6)=1

в) б) 16^5-3х = 0,125^{5х – 6}

г) √x² – x + 3=√3x² – 5x + 6

5.Решить неравенства:

а) lg (0,5x)

б) (1/25)^{2 – x x+1}

6.Решить систему уравнений:

а) х – у=7,

log₂(2x +y)=3.

б) x – y=8,

2^x-3y =16.

Вариант – 2

1. Выразить в радианной мере величины углов:

а) 80⁰; б) 130⁰; в) 250⁰; г) 310⁰

1. Выразить в градусной мере величины углов:

а) 7π/4; б) 3π/2; в) 5π/6; г) 4π/3

1. Вычислить:

1. 2sin π/2 + 3cos² π/4=

2. 6sin7π/6 – 4cos4π/3 + 5tg²5π/3=

1. Решить уравнения:

а) sin3x=1/2

б) √3tg(x/3 – π/3)=1

в) 2•5^x+2 – 10•5^x = 8

г) log₃(4 – 2x) - log₃2=2

5.Решить неравенства:

а) log₇(2x – 1)

б) 10^3x+1 0,001

6.Решить систему уравнений:

а) x + y=3,

5^x+3y = 1/5.

б) 3x + y=3,

log₃(5x+4y)=log₃(y+5).

Контрольная работа № 4.

Время выполнения: 90мин

Условия выполнения (используемые справочники, таблицы, наличие раздаточного материала): справочные плакаты

Вариант – 1 Вариант - 2

1. Вычислить производные:

а) у = 2соs(1/2x - 2π) a) y = x⁷ – 4x⁵ + 13x - 67

б) y = x⁵ – 21/3x³ + 6x - 7 б) y = 3sin(2/3x + π/2)

в) y = (x³ – 3x)/(1+4x⁵) в) y = (3x + x³)(2x – 3)

2. Найти промежутки возрастания и убывания функции:

а) f(x) = 3x² – 2x³ + 6 a) f(x) = 3x⁴ – 4x³ + 2

б) f(x) = 2x³ + 9x² – 24x б) f(x) = 2x³ - 3x² – 36

3. Найти наибольшее и наименьшее значения функции:

a) f(x) = 1+8x – x² на промежутке a) f(x)=3x² – 12x + 1 на

[2;5] промежутке [1;4]

4. Исследовать функцию с помощью производной и построить ее график:

а) f(x) = 2/5x⁵ – 2/3x³ а) f(x) = 3/2x² – 4/5x⁵

1. Найти все первообразные функций:

а) f (x) = 6+x⁴ – 3x² а) f (x) = 2x³ – 16x² + 4x – 1

б) f (x) = 2sin x + 14cos x – 9 б) f (x) = 12 – 3sin x – 3cos x

1. Найти площадь фигуры, ограниченной графиком данной функции и прямыми:

а) f (x) = 4 + 6x², y = 0, x = -1, x = 2 а) f (x) = x2 – 3, y = 0, x = -2, x = 3

1. Вычислить интегралы:

а) ∫(5x – 0,5x² – 4)dx а) ∫(x3 + 3x2 – 8x)dx

_{2 3}

б) ∫(2x³ – 6x²)dx б) ∫(4x³ – 3x²)dx

^{-1 -2}

Итоговая контрольная работа

Время выполнения: 90мин

Условия выполнения (используемые справочники, таблицы, наличие раздаточного материала): справочные плакаты

1 вариант

1. Решите неравенство 10^2+x .

2. Решите уравнение 27^{1 - х} =1/81.

3. Найдите производную функции f(х)= е^х(х² + 1).

4. Решите уравнение √ 3х² – 4х – 2 = √ 2х² – 2х + 1.

5. (1 балл) Найдите все первообразные функции f(x)=x⁴ + 3x² + 5.

6. Точки M и N расположены на ребрах четырехугольной пирамиды (рис.1). Скопируйте рисунок, отметьте и постройте точку, в которой прямая MN пересекает плоскость основания пирамиды.

Рис.1

1. Решите неравенство log₅(3х + 1)

2. Решите уравнение 2sin( π/3 – х)=1.

3. Высота цилиндра равна 6см, а площадь его боковой поверхности вдвое меньше площади его полной поверхности. Найдите объем цилиндра.

2 вариант

1. Решите неравенство log₂ (2x + 1) 4.

2. Решите уравнение cos (π + x) = sin π/2.

3. Найдите точки экстремума функции f(х) = 2х³ – ½ х⁴ – 8.

4. Найдите первообразную функции f(х) = 4 – х², график которой проходит через точку (- 3; 10).

5. Вычислите 25^1,5 + (0,25) ^{- 0,5} – 81^0,75.

6. Точки K, L, M и N принадлежат ребрам изображенной на рисунке 2 пирамиды. Определите, пересекаются ли прямые KL и MN, отрезки KN и LM.

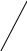
Рис. 2

1. Решите уравнение √ 3х² – 4х – 2 = √ 2х² – 2х + 1.

2. Упростите а^3/4 b^5/24(a^5/12b^-1/8)

3. Найдите площадь сечения шара радиуса 41см плоскостью, проведенной на расстоянии 29см от центра шара.

Критерии оценки письменных контрольных работ обучающихся по математике

Отметка «5» ставится, если:

• работа выполнена полностью;

• в логических рассуждениях и обосновании решения нет пробе­лов и ошибок;

• в решении нет математических ошибок (возможна одна неточ­ность, описка, не являющаяся следствием незнания или непо­нимания учебного материала).

Отметка «4» ставится, если:

• работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);

• допущена одна ошибка или два-три недочета в выкладках, ри­сунках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки).

Отметка «3» ставится, если:

допущены более одной ошибки или более двух-трех недоче­тов в выкладках, чертежах или графиках, но учащийся владеет обязательными умениями по проверяемой теме.

Отметка «2» ставится, если:

допущены существенные ошибки, показавшие, что учащийся не владеет

обязательными умениями по данной теме в полной мере

Отметка «1» ставится, если:

работа показала полное отсутствие у учащегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.

5. КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫЕ МАТЕРИАЛЫ ДЛЯ ПРОВЕДЕНИЯ

ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ

Экзамен

Форма проведения: письменная

Условия выполнения

Время выполнения задания: 4 академических часа

Наименование учебного кабинета, в котором проводится экзамен: Кабинет № 8 Математика

Оборудование учебного кабинета: учебные столы, стулья

Технические средства обучения: ноутбук, проектор, интерактивная доска

Информационные источники, допустимые к использованию на экзамене: справочные плакаты

Пакет экзаменатора:

Раздаточные материалы: варианты экзаменационной работы

Журнал учебной группы

Ведомость учета сдачи экзамена

Министерство образования Ставропольского края

Государственное бюджетное профессиональное образовательное учреждение «Государственный агротехнический колледж» с.Московское

Утверждаю

Заместитель директора по УР

_____________Л.С.Набокова

Экзаменационные задания

по учебной дисциплине ОУД.04 Математика

Профессия: 43.01.09 Повар, кондитер

Рассмотрено и одобрено на заседании П(Ц)К

общеобразовательных дисциплин

Протокол № ____ от ____________

Руководитель __________________

с.Московское

2021г.

1 вариант экзаменационной работы для проведения письменного экзамена по математике

Критерии оценки выполнения работы

Оценка	Число баллов, необходимое для получения оценки
«3» (удовлетворительно)	9 – 14
«4» (хорошо)	15 – 20 (не менее одного задания из дополнительной части)
«5» (отлично)	21 – 30 (не менее двух заданий из дополнительной части)

Обязательная часть

При выполнении заданий 1 – 8 запишите ход решения и полученный ответ.

1. (1 балл) Вычислите (а²b^1/2)^1/4 при а = 7, b = 2.

a^1/2b^9/8

1. (1 балл) Решите неравенство 0,01 ^2+x .

2. (1 балл) Решите уравнение 27^{1 - х} =1/81.

3. (1 балл) Найдите производную функции f(х)= е^х(х² + 1).

4. (1 балл) Решите уравнение √ 3х² – 4х – 2 = √ 2х² – 2х + 1.

5. (1 балл) Найдите все первообразные функции f(x)=x⁴ + 3x² + 5.

6. (1 балл) Один килограмм яблок стоит 78 рублей. Определите, на сколько килограмм яблок хватит 500 рублей, если стоимость 1 кг снизят на 10%.

7. (1 балл) Какая из данных функций у=х + sin x, у = сos x / х, у = tg x/ x, у = сos x + sin x является четной?

Используя график функции у=f(x) (см. рис. 1 ниже), определите и запишите ответ:

1. (1 балл) область определения функции;

2. (1 балл) при каких значениях х f(x) ≥ 3;

3. (1 балл) точки экстремума функции;

4. (1 балл) промежутки возрастания и промежутки убывания функции;

5. (1 балл) наибольшее и наименьшее значения функции. Рис.1

При выполнении заданий 14-18 запишите ход решения и полученный ответ

1. (1 балл) Через точки С и D проведены прямые, перпендикулярные плоскости α, пересекающие ее в точках А и В соответственно. Найдите расстояние между точками С и D, если AC = 3м, BD = 2м, АВ = 2,4м и отрезок СD не пересекает плоскость α.

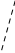
2. (1 балл) Точки M и N расположены на ребрах четырехугольной пирамиды (рис.2). Скопируйте рисунок, отметьте и постройте точку, в которой прямая MN пересекает плоскость основания пирамиды.

Рис.2

1. (1 балл) Тело движется по прямой так, что расстояние S от него до некоторой точки А этой прямой изменяется по закону S = 1 + 4t – t² (м), где t – время движения в секундах. Через какое время после начала движения тело остановится?

2. (1 балл) Решите неравенство log₅(3х + 1)

3. (1 балл) Решите уравнение 2sin( π/3 – х)=1.

Дополнительная часть

При выполнении заданий 19-22 запишите ход решения и полученный ответ

1. (3 балла) Найдите область определения функции y = lg (x² + 4x).

2. (3 балла) Объем конуса с радиусом основания 6см равен 96π см³. Найдите площадь боковой поверхности конуса.

3. (3 балла) Решите систему уравнений х – у = 8,

2^{х – 3у} = 16.

1. (3 балла) Найдите наибольшее и наименьшее значения функции у = 2х³ – 15х² + 24х + 3 на отрезке [2;3].

2 вариант экзаменационной работы для проведения письменного экзамена по математике

Критерии оценки выполнения работы

Оценка	Число баллов, необходимое для получения оценки
«3» (удовлетворительно)	9 – 14
«4» (хорошо)	15 – 20 (не менее одного задания из дополнительной части)
«5» (отлично)	21 – 30 (не менее двух заданий из дополнительной части)

Обязательная часть

При выполнении заданий 1 – 8 запишите ход решения и полученный ответ.

1. (1 балл) Вычислите ^0,5log₇⁹

7

1. (1 балл) Решите неравенство log₂ (2x + 1) 4.

2. (1 балл) Решите уравнение cos (π + x) = sin π/2.

3. (1 балл) Найдите точки экстремума функции f(х) = 2х³ – ½ х⁴ – 8.

4. (1 балл) Найдите первообразную функции f(х) = 4 – х², график которой проходит через точку (- 3; 10).

5. (1 балл) Вычислите 25^1,5 + (0,25) ^{- 0,5} – 81^0,75.

6. (1 балл) Определите, сколько банок краски по 2 кг нужно купить для покраски пола в кабинете математики площадью 6х9м², если на 1м² расходуется 300 граммов краски.

7. (1 балл) Решите уравнение 2^{х + 4} – 2^х = 120.

Используя график функции у=f(x) (см. рис. ниже), определите и запишите ответ:

1. (1 балл) область определения функции;

2. (1 балл) при каких значениях х f(x) 2;

3. (1 балл) промежутки возрастания и промежутки убывания функции;

4. (1 балл) координаты точек графика, в которых касательные к нему параллельны оси абсцисс;

5. (1 балл) наибольшее и наименьшее значения функции.

Рис.1

При выполнении заданий 14-18 запишите ход решения и полученный ответ

1. (1 балл) Точки K, L, M и N принадлежат ребрам изображенной на рисунке 2 пирамиды. Определите, пересекаются ли прямые KL и MN, отрезки KN и LM.

Рис. 2

1. (1 балл) Верхние концы двух вертикально стоящих столбов, удаленных друг от друга на расстояние 3,4м, соединены перекладиной. Высота одного столба 5,8м, другого – 3,9м. найдите длину перекладины.

2. (1 балл) Найдите производную функции f(x)=2х² + sinx.

3. (1 балл) Решите уравнение √ 3х² – 4х – 1 = √ 2х² – 5х – 3.

4. (1 балл) Тело движется по прямой так, что расстояние S от него до начальной точки изменяется по закону S = 5t – 0,5t² (м), где t – время движения в секундах. Найдите скорость тела через 2с после начала движения.

Дополнительная часть

При выполнении заданий 19-22 запишите ход решения и полученный ответ

1. (3 балла) Найдите площадь сечения шара радиуса 41см плоскостью, проведенной на расстоянии 29см от центра шара.

2. (3 балла) Найдите экстремумы функции у = х³ – 3х² – 9х – 4.

3. (3 балла) Найдите координаты общих точек графиков функций у = 2х – 7 и у = √ 2х – 1.

4. (3 балла) Решите систему уравнений 3х + у = 3,

log₃ (5x + 4y) = log₃ (y + 5).

3 вариант экзаменационной работы для проведения письменного экзамена по математике

Критерии оценки выполнения работы

Оценка	Число баллов, необходимое для получения оценки
«3» (удовлетворительно)	9 – 14
«4» (хорошо)	15 – 20 (не менее одного задания из дополнительной части)
«5» (отлично)	21 – 30 (не менее двух заданий из дополнительной части)

Обязательная часть

При выполнении заданий 1 – 8 запишите ход решения и полученный ответ.

1. (1 балл) Упростите а^3/4 b^5/24(a^5/12b^-1/8)

2. (1 балл) Решите уравнение 3^х+2 - 5·3^х =36.

3. (1 балл) Решите уравнение sin x/2 +1=0.

4. (1 балл) Найдите значение производной функции f(x) = tg x – 2sin x при х=-π/4.

5. (1 балл) Билет на автобус стоит 70 рублей. Определите, на сколько поездок хватит 600 рублей, если стоимость билета снизят на 10%.

6. (1 балл) Решите неравенство log_0,5(2x)2.

7. (1 балл) Вычислите 16^5/4 – (1/9)^-1/2 + 27^2/3 .

8. (1 балл) Найдите все первообразные функции f(x)= 3х⁴ – 1.

Используя график функции у=f(x) (см. рис. ниже), определите и запишите ответ:

1. (1 балл) область определения функции;

2. (1 балл) при каких значениях х f(x)

3. (1 балл) промежутки, на которых производная принимает положительные, отрицательные значения;

4. (1 балл) наибольшее и наименьшее значения функции.

Рис.1

При выполнении заданий 13-18 запишите ход решения и полученный результат

1. (1 балл) Точки K, L, M и N принадлежат ребрам изображенной на рисунке 2 пирамиды. Определите, пересекаются ли отрезки KN и LM.

Рис.2

1. (1 балл) Вычислите 3^2log₉¹².

2. (1 балл) Найдите площадь фигуры, ограниченной графиком функции f (x) = x² – 6х + 8, прямыми х= -2, х=-1 и осью абсцисс.

3. (1 балл) Решите неравенство lg (2x + 1)

4. (1 балл) Решите уравнение ½ √ х + 1 = 4.

5. (1 балл) Найдите sin x, если cos x = 0,6, 0

Дополнительная часть

При решении заданий 19-22 запишите ход решения и полученный ответ

1. (3 балла) Образующая конуса равна 5см, площадь его боковой поверхности равна 15π см². Найдите объем конуса.

   

2. (3 балла) Решите уравнение 2 cos² x – cos x – 1 = 0.

3. (3 балла) Решите систему уравнений х + у = 3,

5^{х + 3у} = 1/5.

1. (3 балла) Решите уравнение √ 1 + 4х – х² = х – 1.

4 вариант экзаменационной работы для проведения письменного экзамена по математике

Критерии оценки выполнения работы

Оценка	Число баллов, необходимое для получения оценки
«3» (удовлетворительно)	9 – 14
«4» (хорошо)	15 – 20 (не менее одного задания из дополнительной части)
«5» (отлично)	21 – 30 (не менее двух заданий из дополнительной части)

Обязательная часть

При выполнении заданий 1 – 8 запишите ход решения и полученный ответ.

1. (1 балл) Вычислите (27^2/5·2^1/5·2)^5/6.

2. (1 балл) Решите неравенство 10^{3х +1} 0,001.

3. (1 балл) Решите уравнение 2sin x – sin²x = cos²x.

4. (1 балл) Найдите производную функции f(x)=x²lnx.

5. (1 балл) Решит уравнение 25^1-3х = 1/125.

6. (1 балл) Точки K, L, M и N принадлежат соответствующим ребрам куба, изображенного на рисунке 1. Определите, пересекаются ли прямые KL и MN, отрезки KN и LM.

Рис. 1

1. (1 балл) Определите, сколько банок краски по 3кг необходимо купить для покраски пола в спортивном зале площадью 6х12м², если на 1м² расходуется 300 граммов краски.

2. (1 балл) Вычислите (3lg2 + lg0,25) : (lg14 – lg7).

Используя график функции у=f(x) (см. рис. ниже), определите и запишите ответ:

1. (1 балл) область определения функции;

2. (1 балл) при каких значениях х f(x) ≤ 0;

3. (1 балл) точки экстремума функции;

4. (1 балл) промежутки возрастания и убывания функции;

   

5. (1 балл) наибольшее и наименьшее значение функции. Рис.2

При выполнении заданий 14-18 запишите ход решения и полученный результат

1. (1 балл) Найдите значение производной функции f(x) = 3х + √х при х = 16.

2. (1 балл) От электрического столба высотой 6м к дому, высота которого 3м, натянут кабель. Определите длину кабеля, если расстояние между домом и столбом 4м.

3. (1 балл) Тело движется по закону S(t) = t² – 7t + 3 (м), где t – время движения в секундах. Определите, в какой момент времени скорость будет равна 3.

4. (1 балл) Решите уравнение 5^{5х + 1} = 25^2х.

   

5. (1 балл) На рисунке 3 изображены параллельные плоскости α и β. Точки А и В принадлежат плоскости α, а точка С лежит в плоскости β, а точка М принадлежит прямой ВС. Скопируйте рисунок и изобразите на нем точку D, принадлежащую плоскости β, так, чтобы прямые AD и BC пересекались в точке М.

В

Дополнительная часть

При выполнении заданий 19-22 запишите ход решения и полученный ответ

1. (2 балл) Найдите какую-нибудь первообразную функции f (x) =4 + 6х², значение которой при х = 2 отрицательно.

2. (3 балла) Осевым сечением цилиндра является квадрат, диагональ которого равна 6√2 см. Найдите площадь полной поверхности цилиндра.

   

3. (3 балла) Решите систему уравнений 4х + у = - 10,

log₃ (3y – x) = 2.

1. (3 балла) Найдите экстремумы функции у = х³ – 3х² – 9х – 4.

Критерии оценки результатов экзамена

При проверке математической подготовки обучающихся, сдающих экзамен по математике, оценивается уровень сформированности следующих умений:

• выполнять арифметические действия, сочетая устные и письменные приемы; находить значения корня натуральной степени, степени с рациональным показателем, логарифма;

• проводить по известным формулам и правилам преобразование буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;

• вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;

• определять значения функции по значению аргумента при различных способах задания функции;

• строить графики изученных функций; описывать по графику поведение и свойства функций, находить по графику функции наибольшее и наименьшее значения;

• решать уравнения, простейшие системы уравнений, используя графики функций;

• вычислять производные и первообразные элементарных функций;

• исследовать в простейших случаях функции на монотонность, находить наибольшее и наименьшее значения функций, строить графики многочленов с использованием аппарата математического анализа;

• решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, их системы;

• анализировать в простейших случаях взаимное расположение объектов в пространстве;

• изображать основные многогранники и круглые тела; выполнять чертежи по условиям задач;

• решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов);

• использовать при решении стереометрических задач планиметрические факты и методы;

• проводить доказательные рассуждения в ходе решения задач.

Инструкция для обучающихся

На выполнение письменной экзаменационной работы по математике дается 4 астрономических часа (240минут).

Экзаменационная работа состоит из двух частей: обязательной и дополнительной. Обязательная часть содержит задания минимально обязательного уровня, а дополнительная часть – более сложные задания.

При выполнении большинства заданий обязательной части требуется представить ход решения и указать полученный ответ, и только в нескольких заданиях достаточно представить ответ.

При выполнении любого задания дополнительной части описывается ход решения и дается ответ.

Правильное выполнение заданий оценивается баллами, баллы указываются в скобках около номера задания. Правильное выполнение любого задания обязательной части оценивается 1 баллом, правильное выполнение каждого задания дополнительной части – 3 баллами.

Баллы, полученные за все выполненные задания, суммируются.

Постарайтесь выполнить как можно больше заданий и набрать как можно больше баллов.

Перед началом работы внимательно изучите критерии оценивания и обратите внимание, что начинать выполнять работу следует с заданий обязательной части. И только после того, как Вы наберете необходимое количество баллов для удовлетворительной оценки, можете переходить к заданиям дополнительной части, чтобы повысить оценку до «4» или «5».

Желаем успехов!