Кейс "Сравнение величин. Размеры.Единицы измерения. Чтение и анализ графиков и диаграмм"

Сравнение величин. Размеры. Единицы измерения.

Задание №2 ЕГЭ математика (базовый уровень).

В задании №2 ЕГЭ необходимо установить соответствие между величинами и их возможными значениями. Для успешного выполнения этого задания необходимо хорошо ориентироваться в единицах измерения различных величин.

В заданиях этого типа встречаются следующие величины: время, длина (в том числе ширина, высота и расстояние между объектами), площадь, объём, масса, скорость (в том числе частота обращения).

Выучить наизусть соотношения единиц измерения различных величин очень полезно, но недостаточно. Ещё обязательно надо представлять примеры из своей жизни, где используются те или иные единицы измерения.

В вопросе не указано, в порядке возрастания или убывания надо записать ответ, поэтому можно записать и 32, и 23. Но лучше приучиться записывать ответ в порядке возрастания.

!!!Следует учитывать, что ответ в виде последовательности цифр на экзамене записывается в бланк ответов без пробелов, запятых и других дополнительных знаков.

1. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.

ВЕЛИЧИНЫ

А)  рост ребёнка

Б)  толщина листа бумаги

В)  длина автобусного маршрута

Г)  высота жилого дома

ВОЗМОЖНЫЕ ЗНАЧЕНИЯ

1)  32 км

2)  30 м

3)  0,2 мм

4)  110 см

А	Б	В	Г

Запишите в ответ цифры, расположив их в порядке,

соответствующем буквам:

Решение. Рост ребёнка может быть равен 110 см, толщина листа бумаги может составлять 0,2 мм, длина автобусного маршрута  — 32 км, высота жилого дома  — 30 м. Ответ: 4312.

2. Установите соответствие между названиями величин, встречающихся в русских пословицах и поговорках, и их приближёнными значениями:

ВЕЛИЧИНЫ

А)  От горшка два вершка

Б)  Косая сажень в плечах

В)  Семь вёрст не круг

Г)  Будто аршин проглотил

ПРИБЛИЖЁННЫЕ ЗНАЧЕНИЯ

1)  2,5 м

2)  9 см

3)  70 см

4)  7 км

А	Б	В	Г

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

Решение. Напомним меры длины: вершок  — примерно 4,5 см, аршин  — около 70 см, верста  — чуть больше километра, косая сажень  — примерно 2,5 м. Получим соответствие А - 2, Б -1, В - 4 и Г - 3. Окончательно получим 2143.

Чтение и анализ графиков, диаграмм и таблиц.

Задание №3 ЕГЭ математика (базовый уровень).

В задании №3 ЕГЭ вам предстоит определять значение величины, используя информацию, представленную в виде графика, диаграммы или таблицы.

!!! При выполнении этого задания крайне важно внимательно прочитать условие задачи и вопрос к ней, а также необходимо внимательно рассмотреть и проанализировать график, диаграмму или таблицу, представленную в задаче.

Рекомендую подчеркивать в тексте задачи в КИМе то, о чём спрашивается. В некоторых задачах могут спросить, например, о наибольшей величине какого-то показателя за весь указанный период времени, а в других – только за первую половину дня или за третий квартал года.

!!! Квартал – четвертая часть года Номера месяцев

Первый квартал – период с января по март Январь - 1

Второй квартал – период с апреля по июнь Февраль - 2

Третий квартал – период с июля по сентябрь Март - 3

Четвертый квартал – период с октября по декабрь Апрель - 4

Первая половина года период с января по июнь Май - 5

Вторая половина года период с июля по декабрь Июнь - 6

Первая половина дня - до 12:00 часов Июль - 7

Вторая половина дня - после 12:00 часов Август - 8

Утро - с 6:00 до 12:00 часов Сентябрь - 9

День - с 12:00 до 18:00 часов Октябрь - 10

Вечер - с 18:00 до 0:00 часов Ноябрь - 11

Ночь - с 0:00 до 6:00 часов Декабрь - 12

1. На диаграмме показано количество осадков за год, выпавших в некотором городе. По горизонтали указаны месяцы, по вертикали —количество выпавших осадков в миллиметрах. Определите по диаграмме наибольшее количество осадков, выпавших за месяц в этом городе в течение года. Ответ дайте в миллиметрах.

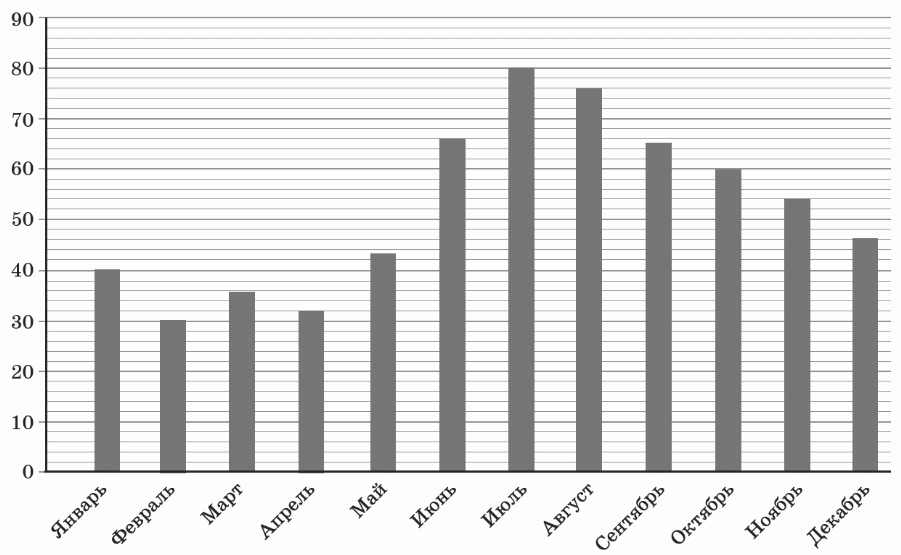
1. На диаграмме показано количество осадков за год, выпавших в некотором городе. По горизонтали указаны месяцы, по вертикали —количество выпавших осадков в миллиметрах. Найдите по диаграмме разность между наибольшим и наименьшим значениями количества выпавших осадков за месяц в первом квартале года. Ответ дайте в миллиметрах.

2. На графике показан процесс разогрева двигателя легкового автомобиля. На оси абсцисс откладывается время в минутах, прошедшее от запуска двигателя, на оси ординат  — температура двигателя в градусах Цельсия. Определите по графику, сколько минут двигатель нагревался от температуры 60 °C до температуры 90 °C.

1. В таблице представлены налоговые ставки на автомобили в Москве с 1 января 2013 года.

Мощность автомобиля (в л. с.*)	Налоговая ставка(руб. за 1 л. с.* в год)
не более 70	0
71–100	12
101–125	25
126–150	35
151–175	45
176–200	50
201–225	65
226–250	75
свыше 250	150

 *л. с.  — лошадиная сила.

Какова налоговая ставка (в рублях за 1 л. с. в год) на автомобиль мощностью 115 л. с.?