Алгоритмы и их применение на уроках математики

МБОУ Киселевская СОШ им. Н.В. Попова

Разработка интегрированного урока математики и информатики

в 10 классе:

Зайцевой Людмилы Михайловны

учителя математики и информатики

высшая квалификационной категории

Тема урока: «Алгоритмы и их применение на уроках математики».

Цель урока:

• закрепить и обобщить представления учащихся об алгоритмах на основе использования задач математики:

Основные задачи урока:

образовательные:

• формировать умения составлять алгоритмы при решении математических задач

развивающие:

• способствовать развитию приемов алгоритмического мышления;

• способствовать развитию интеллекта.

мотивационные:

• развивать познавательный интерес;

• способствовать применению полученных знаний и умений в различных информационных ситуациях.

воспитательные:

• формировать культуру умственного труда и умение планировать свою работу, рационально её выполнять;

• способствовать развитию настойчивости и целеустремлённости, творческой активности и самостоятельности, способности аргументировать свои убеждения.

Тип урока

• Интегрированный - на закрепление полученных знаний

• Урок обобщения и систематизации знаний.

Форма урока:

Сюжетный урок – практическое занятие с элементами беседы познавательного характера

Знать:

1. Понятие алгоритма

2. Виды алгоритмов

3. Понятие пошагового исполнения алгоритма

4. ППО для выполнения практических заданий

Уметь:

1. Быть «исполнителем» алгоритмов

2. Анализировать полученные результаты

3. Достигать цели с минимальными затратами

Методы:

1. Игровой

2. Наглядный

3. Иллюстративный.

4. Поисковый

Оборудование:

• доска,

• раздаточный материал,

• компьютер,

• компьютерная презентация.

План урока:

• Орг. момент.

• Сообщение темы и цели урока

• Проверка знаний (тест)

• Задания- разминка.

• Практическая часть.

• Самостоятельная работа

• Разгадайте кроссворд

• Кто быстрее?

• Итоги урока

• Домашнее задание

• Вопросы учеников

• Дополнительная задача

Ход урока:

I. Орг. момент.

Приветствие, проверка присутствующих. Объяснение хода урока.

2. Сообщение темы и цели урока ( Актуализация знаний.)

Для решения большинства задач существует множество готовых программ. Но для того чтобы лучше понимать все происходящее с компьютером и уверенно принимать правильные решения, рядовому пользователю необходимо обладать определенной компьютерной грамотностью.

Следует отметить, что большинство редакторов (например, Microsoft Office Word, Excel) имеют встроенные средства программирования, освоив которые можно значительно расширить свои возможности

Чтобы тему сегодняшнего урока узнать,
Вам нужно данную шифрограмму разгадать.

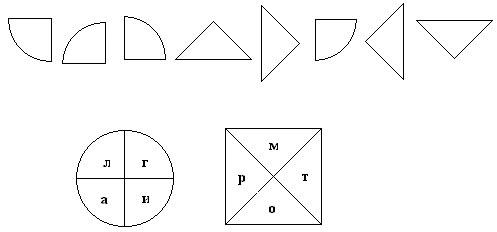
– Тема урока: «Алгоритмы. И их применение на уроках математики»

3. Проверка знаний.

Для того чтобы вспомнить тему предыдущего урока ответьте на вопросы небольшого теста. Учащиеся выполняют тест.

Ничего не говорите, только «да» или «нет» напишите :

Утверждения для 1 варианта

Утверждения для 2 варианта

.Алгоритм ветвления обязательно содержит условие, которое может выполниться или не выполниться В алгоритме ветвления направление решения задачи зависит от выполнения или невыполнения условия В линейном алгоритме последовательность команд выполняется многократно Линейный алгоритм является частным случаем алгоритма ветвления Число повторений для цикла с параметром нельзя вычислить заранее Тело цикла с параметром не может содержать ветвление Параметр цикла может принимать только положительное значение Шаг в цикле с параметром обязательно должен принимать целое значение В цикле с параметром начальное значение параметра всегда должно быть меньше конечного Любая последовательность действий является алгоритмом Строгая последовательность конечного числа действий является алгоритмом

Алгоритм должен обязательно выполняться за конкретное число шагов Форма представления алгоритма зависит от исполнителя Если задачу можно разбить на отдельные шаги (действия), то для нее можно составить алгоритм Графический способ представления алгоритма используется для исполнителя-человека Словесный способ представления алгоритма более нагляден по сравнению с графической формой Алгоритмизация — обязательный этап для решения задачи с использованием компьютера Программу – это способ задания алгоритмов Исполнитель алгоритма выполняет только те команды, которые входят в состав его команд Дискретность является необязательным свойством алгоритма Свойство "результативность" указывает на получение результата за конечное число шагов Программа — способ описания алгоритма для исполнителя-компьютера

1	2	3	4	5	6	7	8	9	10	11

Критерии оценки тестов:

Для теста из 11 вопросов:

• 9–11 правильных ответов – оценка “5”;

• 7–8 правильных ответов – оценка “4”;

• 4–6 правильных ответов – оценка “3”;

• меньше 4 правильных ответов – оценка “2”.

4. Теоретическая часть.

В 1983 году отмечалось 1200-летие со дня рождения одного из величайших ученых Средней Азии и средневекового Востока Мухамада ибн Мусы аль-Хорезми. Он написал ряд трактатов по арифметике и алгебре, в том числе книгу "Арифметика индусскими цифрами" – о счете с помощью десяти цифр и правилах арифметических действий с числами.

Имя ученого аль-Хорезми превратилось в понятие algorithmi, первоначально обозначавшее десятичную систему исчисления и правила арифметических действий в этой системе. Отсюда и возник современный научный термин "алгоритм".

Каждый из нас ежедневно использует различные алгоритмы: инструкции, правила, рецепты и т.п. Обычно мы это делаем не задумываясь. Например, открывая дверь ключом, никто не размышляет над тем, в какой последовательности выполнять действия. Однако чтобы научить кого-нибудь открывать дверь, придется четко указать и сами действия, и порядок их выполнения. То же потребуется и при указании маршрута поездки.

Сравним эти алгоритмы. На первый взгляд, между ними нет ничего общего. Одно дело – открывать дверь, другое – ехать в гости. Но если приглядеться внимательно, можно заметить существенное сходство между ними. Прежде всего, это строгий порядок выполнения действий

1. Достать ключ из кармана.

2. Вставить ключ в замочную скважину.

3. Повернуть ключ два раза против часовой стрелки.

4. Вынуть ключ.

Если вы внимательно оглянитесь вокруг, то обнаружите множество алгоритмов которые мы с вами постоянно выполняем. Мир алгоритмов очень разнообразен. Несмотря на это, удается выделить общие свойства, которыми обладает любой алгоритм.

Свойства алгоритмов:

1. Дискретность (алгоритм должен состоять из конкретных действий, следующих в определенном порядке);

2. Детерминированность (любое действие должно быть строго и недвусмысленно определено в каждом случае);

3. Конечность (каждое действие и алгоритм в целом должны иметь возможность завершения);

4. Массовость (один и тот же алгоритм можно использовать с разными исходными данными);

5. Результативность (отсутствие ошибок, алгоритм должен приводить к правильному результату для всех допустимых входных значениях).

Виды алгоритмов:

1. Линейный алгоритм (описание действий, которые выполняются однократно в заданном порядке);

2. Циклический алгоритм (описание действий, которые должны повторятся указанное число раз или пока не выполнено задание);

3. Разветвляющий алгоритм (алгоритм, в котором в зависимости от условия выполняется либо одна, либо другая последовательность действий)

4. Вспомогательный алгоритм (алгоритм, который можно использовать в других алгоритмах, указав только его имя).

Для более наглядного представления алгоритма широко используется графическая форма - блок-схема, которая составляется из стандартных графических объектов.

Стадии создания алгоритма:

1. Алгоритм должен быть представлен в форме, понятной человеку, который его разрабатывает.

2. Алгоритм должен быть представлен в форме, понятной тому объекту (в том числе и человеку), который будет выполнять описанные в алгоритме действия.

Алгоритм, записанный на «понятном» компьютеру языке программирования, называется программой.

5. Задания - разминка

Определить, что обозначают крылатые фразы:

• «Что, из чего и как?» (Ответ: понятие алгоритма; ученики дают понятие алгоритма)

• «Казнить нельзя помиловать» (Ответ: свойство алгоритма – однозначность)

• «Пойди туда, не знаю куда, принеси то, не знаю, что» (Ответ: свойство алгоритма понятность)

• «Где начало того конца, которым заканчивается начало» (Ответ: вид алгоритма циклический)

• «Налево пойдешь – коня потеряешь, направо пойдешь – убитым быть» (Ответ: вид алгоритма – полное ветвление)

• Я – часть, которая была целым (Ответ: вид алгоритма – вспомогательный; метод пошаговой детализации)

6. Практическая часть.

Линейные алгоритмы:

Простейшие задачи имеют линейный алгоритм решения. Это означает, что он не содержит проверок условий и повторений.

Пример 1.

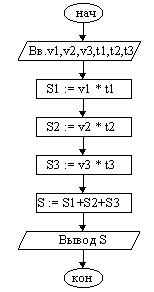
Пешеход шел по пересеченной местности. Его скорость движения по равнине v =1 км/ч, в гору — v =2 км/ч и под гору v=3 км/ч. Время движения соответственно t=1, t=2 и t=3 ч. Какой путь прошел пешеход?

1. Ввести v1, v2, v3, t1, t2, t3. 2. S1 := v1 * t1. 3. S2 := v2 * t2. 4. S3 := v3 * t3. 5. S := S1 + S2 + S3. 6. Вывести значение S. 7. Конец.

Для проверки работоспособности алгоритма необходимо задать значения входных переменных, вычислить конечный результат по алгоритму и сравнить с результатом ручного счета.

Пример 2. Рассмотрим для примера программу вычисления площади треугольника по 3 сторонам.

, где

Составим алгоритм и запишем его в виде блок-схемы:

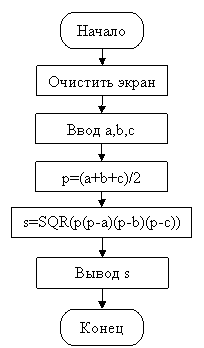
Все операторы этой программы выполняются друг за другом, т.е. программа имеют линейную структуру.

Развилка: Достаточно часто то или иное действие должно быть выполнено в зависимости от значения логического выражения, выступающего в качестве условия. В таких случаях используется развилка.

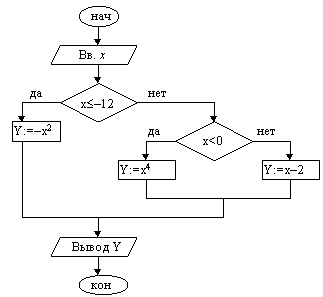
Пример 1. Вычислить значение функции

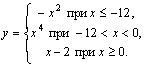
1. Ввести x. 2. Если x–12, то y:=–x2 3. Если x4 4. y := x–2 5. Вывести y 6. Конец

При тестировании алгоритмов с развилкой необходимо подбирать такие исходные данные, чтобы можно было проверить все ветви. В приведенном выше примере должно быть по крайней мере три тестовых набора.

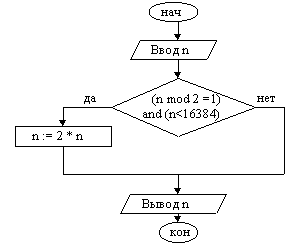
Пример 2. Дано натуральное число n. Если число нечётное и его удвоение не приведет к выходу за 32767 (двухбайтовое целое число со знаком), удвоить его, иначе — оставить без изменения.

Чтобы удовлетворить условию удвоения, число n должно быть нечетным и меньше 16384.

1. Ввести число n 2. Если число n нечетное и меньше 16384, то n := n * 2 3. Вывод n 4. Конец

Рассмотренный пример иллюстрирует неполную развилку. Также следует отметить, здесь логическое выражение, являющееся условием, содержит 2 операнда.

Циклы: Если какие-либо операторы необходимо выполнить несколько раз, то их не переписывают каждый раз заново, а организуют цикл.

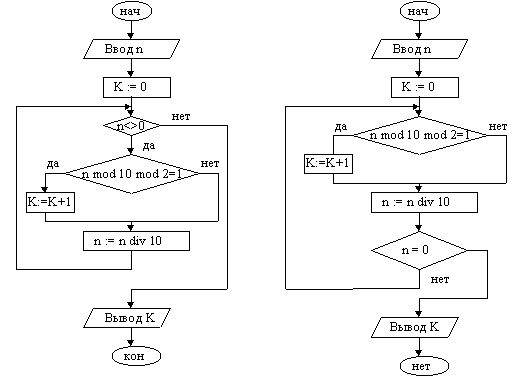
Пример 1. Подсчитать количество нечетных цифр в записи натурального числа n.

Идея решения. Из заданного числа выбирать из младшего разряда цифру за цифрой до тех пор, пока оно не исчерпается, т.е. станет равным нулю. Каждую нечётную цифру учитывать.

1. Ввести число n 2. K := 0 {подготавливаем счётчик} 3. Если n = 0, переход к п. 7 4. Если n mod 10 mod 2 = 1, то K := K +1 5. n := n div 10 6. Переход к п. 3 7. Вывод K 8. Конец

Задача решена двумя способами. Слева решение оформлено с использованием цикла с предусловием, справа — с постусловием.

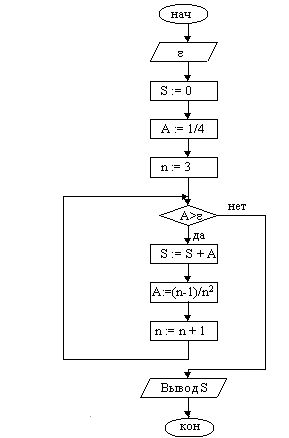
Пример 2. Дана последовательность, общий член которой определяется формулой

Вычислить при n2 сумму тех ее членов, которые больше заданного числа .

При решении задачи находится очередной член последовательно и, если он больше , добавляется к сумме.

1. Ввести  2. S := 0 3. A := 1/4 4. n := 3 5. Сравнить А с . Если A=, переход к п. 10 6. S := S + A 7. A := (n-1)/(n*n) 8. n := n + 1 9. Переход к п. 5 10. Вывод S 11. Конец

В рассмотренных выше примерах количество повторений заранее неизвестно. В первом оно зависит от количества цифр в записи натурального числа, во втором — от числа .

В тех же случая, когда количество шагов известно из условия задачи, проще и предпочтительней использовать цикл с параметром.

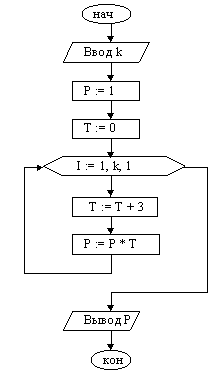
Пример 3. Найти произведение первых k натуральных чисел, кратных трём.

При составлении алгоритма учтем, что первое натуральное число, кратное 3, есть тройка, а все последующие больше предыдущего на 3.

1. Ввод k 2. P := 1 {здесь накапливаем произведение} 3. T := 0 {здесь будут числа, кратные 3} 4. I := 1 5. Если I k, переход к п. 10 6. T := T + 3 7. P := P * T 8. I := I + 1 9. Перейти к п. 5 10. Вывод P 11. Конец

 

7. Самостоятельная работа

На практической части урока вам необходимо будет разработать алгоритм программы для нахождения площади, высоты, диагонали (см. свой вариант задания). Перед написанием программы на компьютере запишите в тетрадь блок-схему ее алгоритма.

ВАРИАНТ 1

 1. Составьте блок-схему и программу вычисления значения функции: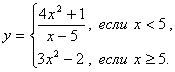

2. Составьте программу, определяющую, является ли данное число делителем числа 3.
3. Составьте блок-схему алгоритма и программу вычисления площади трапеции по сумме оснований и высоте.

ВАРИАНТ 2

1. Составьте блок-схему и программу вычисления значения функции: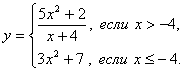

2. Составьте программу, определяющую, является ли данное число кратным 4.

3.Составьте блок-схему алгоритма и программу вычисления площади треугольника по основанию и высоте.
Учащиеся выполняют задание.

8. Разгадайте кроссворд:

По вертикали:

1. Последовательность строк, каждая из которых содержит некоторую команду для компьютера.

По горизонтали:

2.Свойство алгоритма, обозначающее, к чему приводит выполнение алгоритма,

3.Действие, при выполнении которого числовое значение будет записано в ячейку памяти компьютера с определенным именем.

4.Отдельное указание исполнителю выполнить некоторое законченное действие.

5.Последовательность действий, направленных на достижение указанной цели или решение поставленной задачи.

1. 

1. Программа. 2. Результативность. 3. Присвоить. 4. Команда. 5. Алгоритм

9.Кто быстрее?

Помоги роботу заполнить таблицу по заданному алгоритму.

А	3	5	7	8	10	11	12	15	17
Х

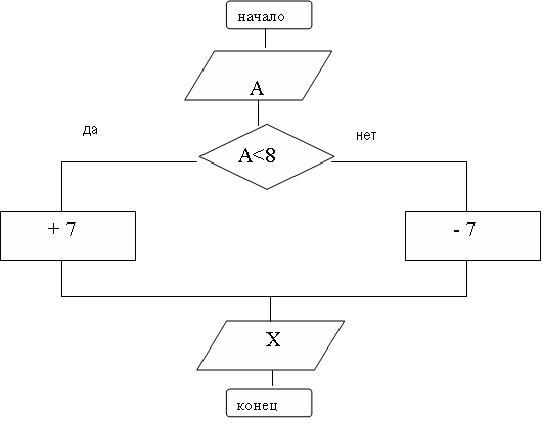
10. Итоги урока.

Подведение итога урока. Выставление оценок.

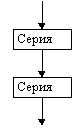
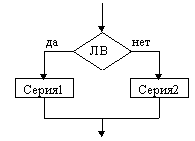
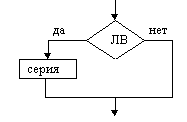
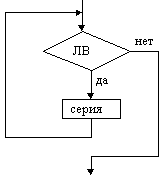
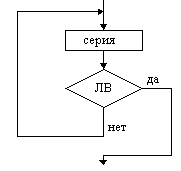
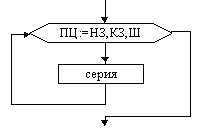
Напомним, что основными алгоритмическими структурами (ОАС) являются следование, развилка и цикл. В более сложных случаях используются суперпозиции (вложения) ОАС.

Ниже приведены графические обозначения (обозначения на блок-схемах) ОАС.

Структура “следование”	Полная развилка	Неполная развилка
Цикл с предусловие (цикл ПОКА)	Цикл с постусловием (цикл ДО)	Цикл с параметром

Вопросы:

• Что такое алгоритм? Приведите примеры алгоритмов.

• Какие свойства алгоритмов вы знаете?

• Какие виды алгоритмов вы знаете?

• Какие способы записи алгоритмов вы знаете?

• Что такое исполнитель алгоритмов?

• Что такое программа?

1. Домашнее задание.

Знать, что такое алгоритм, виды и свойства алгоритмов, уметь составлять программы, имеющие линейную структуру.. Составить программу для вычисления площади треугольника по высоте и основанию. Дополнительное задание: написать программу, описав в ней все используемые переменные. привести примеры алгоритмов из жизненной практики.

Задача. Имеются два кувшина емкостью 3 л и 8 л. Напишите алгоритм на естественном языке, выполняя который можно набрать из реки 7 л воды. (Разрешается пользоваться только этими кувшинами.)

12. Вопросы учеников.

Ответы на вопросы учащихся.

13. Дополнительная задача:

Крестьянин стоит на левом берегу реки с волком, козой и капустой. Ему нужно перевезти все это на правый берег. Но его лодка слишком мала: он может взять только одного пассажира – либо волка, либо капусту, либо козу. Как тут поступить?

Возможные действия крестьянина. В списке четыре строки:

• Перевези волка

• Перевези козу

• Перевези капусту

• Переправься

Все прочие действия запрещены. Рассказанная история приводит нас к еще одному понятию – исполнитель алгоритма и система команд исполнителя.

 

19