Урок по теме " Квадратичная функция"

Урок систематизации и обобщения знаний по теме «Квадратичная функция». 9-й класс. ( Подготовка к ОГЭ).

Образовательные цели:

• обобщить и систематизировать знания учащихся по данной теме;

• повторить определение и основные понятия квадратичной функции;

• рассмотреть ряд примеров;

• закрепить навыки и умения применения знаний по теме к решению упражнений.

Развивающие цели:

• развивать познавательный интерес, навыки коллективной работы;

• применить сформированные знания, умения и навыки в новых ситуациях;

• сформировать навыки взаимоконтроля и самоконтроля.

Воспитательные цели:

• воспитать трудолюбие, аккуратность ведения записей, умение объективно оценивать результаты своей работы;

• прививать желание иметь качественные, глубокие знания, доводить дело до конца.

Тип урока: урок систематизации знаний.

План урока

1. Сообщение темы, целей урока.

2. Проверка знаний фактического материала (теории и практики).

3. Применение знаний в различных конкретных ситуациях.

4. Самостоятельная работа (проверочный тест).

5. Проверка, анализ, оценка самостоятельно выполненных заданий.

6. Сообщение домашнего задания.

7. Итог урока.

Ход урока (40 минут )

1. Организационный момент.

2. Сообщение темы и цели урока.

3. Устная работа: для того чтобы достичь целей урока вспомним теоретический материал по теме «Квадратичная функция»:

   • Функцию какого вида называют квадратичной?

   • Что является графиком квадратичной функции?

   • Назовите квадратичные функции ,которые мы изучили

   • Как зависит направление ветвей параболы от коэффициента а?

   • Как определить координаты вершины параболы?

   • как зависит расположение графика квадратичной функции от D?

   • Можно ли, не выполняя построения графика квадратичной функции, определить промежутки монотонности (т.е. когда функция возрастает, а когда убывает )?

   • Среди заданных функций назовите квадратичные:

1) у = х² ; 2) у = 5- х; 3) у = - 5х; 4) у = 2х+ 3 х² + х; 5) у = - 12 х² + х

Не выполняя построения графика функции у = - 2 х² + 4 х +1, ответить на следующие вопросы:

1) какая это функция;

2) назовите коэффициенты a, b, c;

3) как направлены ветви параболы;

4) какая прямая служит осью параболы;

5) каковы координаты вершины параболы;

6) найдите наибольшее значение функции;

7) назовите координаты точки пересечения ветви параболы с осью ОУ.

4.Решение упражнений

№1 Построим график функции у = 3 х² - 6 х + 2. Определим промежутки монотонности и найдём наименьшее и наибольшее значения функции на [ 0; 3 ].

Решение:

1) у = 3х² - 6 х + 2 – квадратичная функция, графиком которой является парабола;

а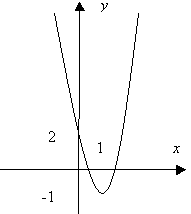 = 3 0, значит, ветви параболы направлены вверх;

2) найдём координаты вершины параболы - ( 1; -1 )

3) дополнительные точки

х	2	3
у	2	11

4) промежутки монотонности:

- функция убывает на (- ; 1]

- функция возрастает на [ 1; +)

5) у_наиб = 11

У_наим = -1

№2. Найти нули функции у = 3 х² - 4 х

Ответ: 0; .

№3 Найдите абсциссы точек пересечения параболы у = х² - 5 х + 4 с осью ОХ.

Ответ: 1; 4.

№ 4. Построить график функции у = -2 х² + 8 х - 1

5.Самостоятельная работа (проверочный тест).

вариант 1

1. Определить коэффициенты квадратичной функции 2у = - х² + 4х + 1

1) -1; 4; 1 2) – 0,5; 2; 0,5 3) -2; 8; 2

2. Найти значение квадратичной функции у = 2х² + 4х + 1 при х = -2

 1) -1 2) -11 3) 1

3. Укажите график функции, который проходит через точку А(1; 2)

1) у = х² – х + 1 2) у = 0,5х² + 3х – 1,5 3) у = -7х² + 4х + 6

4. Найти координаты вершины параболы у = -3х² + 6х + 7

1) (1; 10) 2) (-1; -2) 3) (1; 16)

5. Определить координаты точек пересечения с осью ОХ функции у = х² + 9х + 20

1) (5; 0), (-4; 0) 2) (-4; 0), (-5; 0) 3) (4; 0), (5; 0)

вариант 2

1. Определить коэффициенты квадратичной функции-2у = х² – 4х – 2

1) 1; -4; -2 2) -2; 8; 4 3) -0,5; 2; 1

2. Найти значение квадратичной функции у = -3х² – 4х – 2 при х = -2

1) -6 2) 4 3) -4

3. Укажите график функции, который проходит через точку А(1; 2)

1) у = х² + х + 1 2) у = 2х² – 4 3) у = -3х² + 7х –2

4. Найти координаты вершины параболы у = 3х² - 12х + 1

1) (-2; 37) 2) (2; -11) 3) (2; 11)

5. Определить координаты точек пересечения с осью ОХ функции у = х² - 8х + 15

1) (3; 0),(5; 0) 2) (0; 3), (0; 5) 3) (-3; 0), (-5; 0)

ответы

	ВI	ВII
1	2	3
2	3	1
3	2	3
4	1	2
5	2	1

 

Критерии оценки:

• “5” - 5 заданий;

• “4” - 4 задания;

• “3” - 3 задания.

6. Сообщение домашнего задания.

1. Дана функция y = f ( x ), где f ( x ) = - 4х² - 12х + 40

1) Найти f ( 0 ),  f ( 1 ), f ( -1 )

2) написать уравнение оси симметрии параболы

3) определить координаты точек пересечения параболы с осью ОХ

4) найти все х, при которых у 0

5) указать промежутки монотонности функции.

2. Построить графики заданных функций

1) у = - ( х – 2 )² + 4 2) у =

7. Итог урока.