Тест поматематике (алгебра и н. м. а.) «Первообразная», 11 класс
Вариант 1
1. Найдите производную функции y = 3sin3xв точке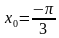
| 1) 4,5; | 2) -9; | 3) -4,5; | 4) свой ответ. |
2. Найдите промежутки убывания функции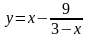
| 1) (-∞; 0)∪(6; +∞); | 2) (0; 6); | 3) (0; 3)∪(3; 6); | 4) свой ответ. |
3. Какая из данных функций является первообразной для функцииy=3x3–2x?
| 1) | 2) x4–x2; | 3) x4–2x2+3; | 4) таких нет. |
4. Какая из данныхфункций является первообразной для функции y=1–2cos2x?
| 1) x | 2) x+cos3x; | 3) | 4) 2– |
5. На каком из указанных промежутков функцияF(x)=2sinx–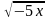 –3является первообразной для функцииf(x)= 2cosx–
–3является первообразной для функцииf(x)= 2cosx–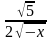 ?
?
| 1) [0; π); | 2) (-π; 0); | 3) (-∞; 0]; | 4) (-∞; 0). |
6. Для функции y=3+4x3найдитепервообразную, график которой проходит через точку М(1; 1)
| 1) y=x4+3x–3; | 2) y=x4; | 3) y=4x4+3x–7; | 4) свой ответ. |
7. Известно, что F1, F2,F3– первообразные дляf(x)=3x5–5на R, графикикоторых проходят через точкиM(1; –3), N(–1; 6),K(2; –4)соответственно. Перечислите, в каком порядке (сверху вниз) графики этих функций пересекают ось ординат?
| 1) F3, F1 ,F2; | 2) F3, F2, F1; | 3) F1, F3, F2; | 4) F1, F2, F3. |
8. Материальная точка движется прямолинейно со скоростьюv(t)=6t2–4t. Найдите закон движения точки, если в момент времени t=0она была в начале координат.
| 1) s(t)=4t3–6t2–2; | 2) s(t)=2t3–2t2; | 3) s(t)=t3–t2; | 4) свой ответ. |
9. Какое расстояние пройдет материальная точка (см. задание 8) за первые 2 секунды своего движения?
| 1) 32 м; | 2) 8 м; | 3) 4 м; | 4) свой ответ. |
10. Найдите наименьшее значение первообразной функции y=4x–3, проходящей через точку(1; 1).
| 1) 0,875; | 2) 0,625; | 3) 0,425; | 4) свой ответ. |
Ключ к тесту:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|
|
|
|
|
|
|
|
|
|
|
Тест поматематике (алгебра и н. м. а.)«Первообразная», 12 класс
Вариант 2
1. Найдите производную функции y = ctg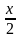 в точке
в точке 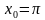 .
.
| 1) – | 2) -1; | 3) | 4) свой ответ. |
2. Найдите промежутки возрастания функции 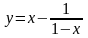
| 1) (-∞; 0]∪(2; +∞); | 2) (0; 2); | 3) (0; 1)∪(1; +∞); | 4) свой ответ. |
3. Какая из данных функций является первообразной для функции y=7x6–15x4?
| 1) 2x7–5x3; | 2) x7–x5–1; | 3) x7–3x5–5,5; | 4) таких нет. |
4. Какая из данных функций является первообразной для функции
y=–4sin2x?
| 1) 2cos2x+2; | 2) 2cos2x+2; | 3) sin4x; | 4) 1–2cos2x. |
5. На каком из указанных промежутков функция F(x)=ctgx–2x–2является первообразной для функции f(x)= –2–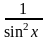 ?
?
| 1) | 2) | 3) (0; 2π); | 4) |
6. Для функции y=–3x2+2 найдите первообразную, график которой проходит через точку М(1; 5)
| 1) y= –3x2+2x+4; | 2) y= –3x3+2x+5; | 3) y= –x3+2x+4; | 4) свой ответ. |
7. Известно, что F1, F2, F3– первообразные для f(x)=4x3+2x+1 на R, графики которых проходят через точки M(0; 0), N(2; -5), K(1; 4) соответственно. Перечислите, в каком порядке (сверху вниз) графики этих функций пересекают ось ординат?
| 1) F1, F2 ,F3; | 2) F1, F3, F2; | 3) F3, F1, F2; | 4) свой ответ. |
8. Материальная точка движется прямолинейно со скоростью v(t)=8t–4. Найдите закон движения точки, если в момент времени t=2cпройденный путь составил 4 м.
| 1) s(t)=4t2–4t–4; | 2) s(t)=t2–t+2; | 3) s(t)=8t2–4t–20; | 4) свой ответ. |
9. Какое расстояние пройдет материальная точка (см. задание 8) за первые 3 секунды своего движения?
| 1) 24 м; | 2) 20 м; | 3) 16 м; | 4) свой ответ. |
10. Найдите наименьшее значение первообразной функции y=6–2x, проходящей через точку (3; 1).
| 1) 10; | 2) 1; | 3) 12; | 4) свой ответ. |
Ключ к тесту:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|
|
|
|
|
|
|
|
|
|
|

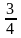
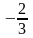 cos
cos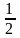
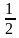 ;
;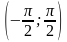 ;
;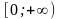 ;
;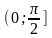 .
.



