6
УРОК МАТЕМАТИКИ В 6 КЛАССЕ:
«СВОЙСТВА ДЕЙСТВИЙ С РАЦИОНАЛЬНЫМИ ЧИСЛАМИ»
Цели урока:
1. Проверить, выполняются ли свойства действий над числами при работе с рациональными числами.
2. Содействовать формированию интеллектуальной, исследовательской культур учащихся (умению анализировать, конкретизировать, творчески мыслить, обобщать полученные знания, размышлять и рассуждать).
3. Развивать коммуникативные способности учащихся (умение работать в парах, обучаться в сотрудничестве, вести монолог и диалог).
4. С помощью интересных форм работы повысить активность учащихся на уроке, добиться сознательного усвоения материала.
5. Работать над повышением грамотности устной и письменной речи учащихся.
Задачи урока:
1. Систематизировать знания учащихся о свойствах рациональных чисел.
2. Через повторение изученного материала перевести учащихся к нахождению значения числового выражения, содержащего рациональные числа и знаки « +» и «-».
Информационная составляющая (жизненно важные знания):
применение умений выполнять действия над рациональными числами при дальнейшем изучении курса алгебры.
Знания, используемые в других дисциплинах: физика, информатика, география, химия.
Учебная задача:
«Открытие» свойств действий с рациональными числами
Тип урока. Деловая игра Урок изучения нового материала.
Организационные формы общения: коллективная, самостоятельная, работа в парах.
Оборудование и наглядность: компьютер, мультимедийный проектор, экран, интерактивная презентация, карточки. индивидуальные задания
Структура урока:
| Вид деятельности | № слайдов | мин. |
| 1. Организационный момент. |
| 1 |
| 2. Сообщение задачи и урока. |
| 2 |
| 3. Актуализация опорных знаний. |
| 10 |
| 4. Закрепление пройденного материала. |
| 11 |
| 5. Физкультминутка. |
| 1 |
| 6. Подготовка к ГИА. |
| 10 |
| 7. Задание на дом: в рубрике газеты « знаете ли вы…?» 8 Дом работа |
| 2 2 |
| 8.Подведение итогов урока. Выставление оценок. | 14 | 1 |
ХОД УРОКА
Организационный момент
Проверка готовности учащихся к уроку.
II. Сообщение темы и целей урока
Сегодня необычный урок Я предлагаю провести его в форме деловой игры и девизом нашего урока
Да, путь познания не гладок.
Но знаем мы со школьных лет,
Загадок больше, чем разгадок,
И поискам предела нет!
Мы с вами на уроке должны создать математическую газету то есть, сверстать номер Я – буду главным редактором, а вы ее – корреспондентами, корректорами. Как вы понимаете значение этого слова? Работать будут 2 отдела по направлениям сложение и вычитание рац чисел,2 отдел умножение и деление рациональных чисел.
А газета наша называется «Рациональные числа».
Представляю вам макет газеты, которая состоит из следующих рубрик: «Спрашивают – отвечаем»,
«Новости дня», «Актуальный репортаж», «Проблема дня» Знаете ли вы…?».
III. Актуализация опорных знаний
Устная работа:I колонка
В первой рубрике «Спрашивают – отвечаем» нам нужно проверить правильность информации, которую нам прислали в письмах наши корреспонденты , конверты получат руководители отделов и распределят работу среди сотрудников. Посмотрите внимательно и скажите, какие правила нам нужно вспомнить, чтобы проверить эту информацию. Правильные ответы примеров передать начальнику отдела ,который в свою очередь печатную информацию передает техническому директору
1 пара 1. Правило сложения отрицательных чисел:
«Чтобы сложить два отрицательных числа, не надо:
1) сложить их модули,
2) поставить перед полученным числом знак?????????».
1) – 8,4 + (– 8,4) = 0;
2) (– 2,2) + 3,5 = 1,3;
2. Правило сложения чисел с разными знаками:
«Чтобы сложить два числа с разными и одинаковыми знаками, надо 1) из большего модуля слагаемых вычесть меньший,
2) поставить перед полученным числом знак того слагаемого, модуль которого больше( меньше).
3) – 13 – 8 = – 5;
4) 15 – 18 = – 13;
5) 7,4 – (– 3,2) = 10,6;
1. Правило деления чисел с разными знаками:
«При делении, умножения чисел с разными знаками, надо:
1) разделить модуль делимого на модуль делителя, 2) поставить перед полученным числом знак плюс».
1) (– 6,7) . (– 10) = – 67;
2) – 9 . 6 = – 54;
3) – 3,6 . 1 = –1;2. Правило умножения двух отрицательных чисел:
«Чтобы перемножить два отрицательных числа, очень надо перемножить их модули».
«Чтобы разделить отрицательное число на отрицательное число, надо разделить модуль разности на модуль делителя».
1) (– 6,7) . (– 10) = – 67;
2) – 9 . 6 = – 54;
3) – 3,6 . 1 = –1;
4) – 18 : (– 0,3) = 60;
5) – 3,7 . 0 = – 3,7.
– Молодцы, хорошо справились.
IV. Закрепление пройденного материала
– А сейчас мы переходим к рубрике «Новости дня». Чтобы заполнить эту рубрику, нам необходимо систематизировать знания о числах.
– Какие вы знаете числа? (Натуральные, дробные, целые)
Как мы можем одним словом назвать это множество чисел и я думаю это будет подзаголовок нашей колонки новости дня
См презентацию
Следующая колонка нашей газета « Актуальный репортаж»
–– А теперь перейдем к письменной работе. Открыли тетради, записали18.03.2015 число, классная работа а вот тему урока мы с вами сформулируем после того как каждый отдел редакции выполняет очень ответственную работу .Работаем с рациональными числами и выясним какие отличительные особенности действий с рациональными числами выполняются и применяются, опираясь на знания, полученные ранее с числами
1 исследования и открытия
(задания на слайдах)
Задания корреспондентам отдела сложения и вычитания рац чисел
Какие отличительные особенности действий с рациональными числами выполняются и применяются в математике и в жизни
1)-7+0; 2)0+(-9,7) 3)-1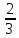 +0; 4)0-(-8).
+0; 4)0-(-8).
1)-7,5+7,5; 2)3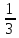 + (-3
+ (-3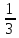 ) 3)-1,25+1
) 3)-1,25+1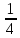
1)-3,2+5=? 2)-8 +(-2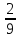 )= 3)8+ (-10)=
)= 3)8+ (-10)=
1)-8+5-2= 2)-6,4-0,6+2,4 3)-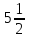 +
+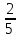 -(0,4)
-(0,4)
Для начальника отдела
-8,125+7,84+9
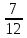 +8
+8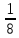 -6,24-9
-6,24-9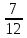
-8
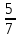 +2
+2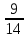 -3
-3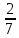 +4
+4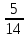 .
.Задания корреспондентам отдела умножения и деления рац чисел
Какие отличительные особенности действий с рациональными числами выполняются и применяются в математике и в жизни.
-12
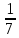 ×0 2)0×(-128,56) 3)0÷(-8,57) 4)-7÷0
×0 2)0×(-128,56) 3)0÷(-8,57) 4)-7÷0
1)13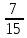 ×1 2)-5,1×(-1) 3)-9×
×1 2)-5,1×(-1) 3)-9×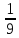 ;
;
1)-6×(-2,4) 2)-5×(-1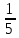 )
)
1)0,2×(-7)×5 2)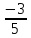 ×50×(-
×50×(-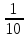 )
)
Для начальника отдела
1 ) (-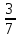 )×(-
)×(-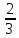 )×
)×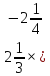 )
)
2)-2,8×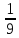 ×(-
×(-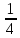 )
)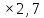
1)Проверка переместительного свойства сложения:
-3 +(- 4) =-4+ (-3) = - 7 a +b = b + a
Вывод: переместительное свойство сложения справедливо при сложении рациональных чисел
2) работа по рядам (проверка сочетательного свойства
(a + b) + c= a + (b + c)
Если 1) a = - 0,7, b = - 0,2, c = 1,2;
(a + b) + c = a + (b + c)
Вывод: сочетательное свойство сложения справедливо при сложении рациональных чисел
3) Прибавление к нулю рационального числа, сумма противоположных чисел:
- 3 ½ + 0 = - 3 ½ а + 0 = а
-1,6 + 1,6 = 0 а + (-а) = 0
Вывод: прибавление нуля к рациональному числу не изменяет это число, а сумма противоположных рациональных чисел равна нулю.
4) Проверка переместительного свойства умножения рациональных чисел:
0,5 * (-2)=* 0,5 = - 1 аb = bа
Вывод: переместительное свойство умножения справедливо при умножении рациональных чисел.
5) Проверка сочетательного свойства умножения рациональных чисел:
- 3 *(4*2,5)= (-,3*4)*2,5 a(bc) = (ab)c
Вывод: сочетательное свойство умножения справедливо при умножении рациональных чисел
6) Умножение рационального числа на единицу, на обратное ему число, на нуль.
- 5/8 * 1 = - 5/8 2 * ½ = 1 4/5 * 0 = 0
а * 1= а а * 1/а = 1 а * 0 = 0
7) Проверка распределительного свойства относительно сложения
(a + b)c = ac +bc, если а = 2 b = - 3 с = - 0,1
Вывод: распределительное свойство относительно сложения справедливо для рациональных чисел.
Свойство а*в=0 если а=0 или в=0
А для чего необходимо знание свойств рациональных чисел? (выполнять вычисления лучше и быстрее).
материал подтвержден в учебнике на стр 207 №1205.(а,в),1209 (а.бв)
Д.М. стр 22 №262,№265(а)
V. Производственная физкультминутка
ГБОУ ЦО 497
VI. Подготовка к ГВЭ
В рубрику «Проблема дня » пришло письмо, где ученик просит помочь ему в решении заданий к и экзамену в 10 классе нашей школы. Нам нужно каждому самостоятельно прорешать задания, тесты Приложение 1 у вас на столах:
1. Решить уравнения:
а) (х + 3)(х – 6) = 0
1) х = 3, х = – 6
2) х = – 3, х = – 6
3) х = – 3, х = 6
б) – 7(3,5 – х) = 0
1) х = 3,5
2) х = – 7
3) х = – 3,5
2. Округлить число 253,355 до десятых:
1) 253,4
2) 253,3
3) 253,35
3. Выберите наименьшее число:
1) – 13,5
2) – 32,8
3) – 40,2
4. Выбери наибольшее число:
1) – 12,4
2) – 43,5
3) – 12,2
5. Расположите в порядке возрастания: ![]()
1) ![]()
2) ![]()
3) ![]()
VII. Задание на дом
– Домашнее задание вы возьмете в последней рубрике нашей газеты « знаете ли вы…?» информация о рац числах приложение
VIII. Подведение итогов урока. Выставление оценок
Вот и получилась у нас вами замечательная математическая газета и как же все таки мы ее назовем. Где мы систематизировали свои знания по теме «Свойства действий с рациональными числами». Приложение 2 И я вам дарю первый выпуск нашей газет это подарок от меня, который будет вам необходим на уроках математики . свойства рац чисел Сегодня тесное сотрудничество в деловой игре я предлагаю оценить себя по лестнице успеха
Что быстрее всего? – Ум.
Что мудрее всего? – Время.
Что приятнее всего? – Достичь желаемого.
– Я думаю, мы с вами достигли желаемого. Спасибо вам большое за урок!
Приложение 3При этом в течение долгого времени многие выдающиеся математики отказывались вводить их в употребление или вводили с большой неохотой. Еще Декарт называл отрицательные числа «ложными числами».
отрицательные числа появились значительно позже натуральных чисел и обыкновенных дробей. Первые сведения об отрицательных числах встречаются у китайских математиков во II в. до н.э. Положительные числа тогда толковались как имущество, а отрицательные как долг, недостача. Но ни египтяне, ни вавилоняне, ни древние греки отрицательных чисел не знали. Лишь в VII в индийские математики начали широко использовать отрицательные числа, но относились к ним с некоторым недоверием. В Европе отрицательными числами начали пользоваться с XII-XIII вв, но до Х//I в. как и в древности , они понимались как долги, большинство ученых считали их ложными в отличие от положительных чисел - истинных. Признанию отрицательных чисел способствовали работы французского математика, физика и философа Рене Декарта (1596-1650) . Он предложил геометрическое истолкование положительных и отрицательных чисел - ввел координатную прямую (1637).
Окончательное и всеобщее признание как действительно существующие отрицательные числа получили лишь в первой половине ХVIII века. Тогда же утвердилось и современное обозначение для отрицательных чисел.

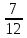 +8
+8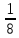 -6,24-9
-6,24-9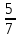 +2
+2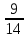 -3
-3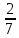 +4
+4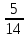 .
.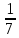 ×0 2)0×(-128,56) 3)0÷(-8,57) 4)-7÷0
×0 2)0×(-128,56) 3)0÷(-8,57) 4)-7÷0



