«Развитие математической грамотности
школьников на уроках математики в начальной школе»
Функционально грамотный человек — это человек, который способен использовать все постоянно приобретаемые в течение жизни знания, умения и навыки для решения максимально широкого диапазона жизненных задач в различных сферах человеческой деятельности, общения и социальных отношений».
А. А. Леонтьев
Математическая грамотность – это способность индивидуума формулировать, применять и интерпретировать математику в разнообразных контекстах. Она включает математические рассуждения, использование математических понятий, процедур, фактов и инструментов, чтобы описать, объяснить и предсказать явления. Она помогает людям понять роль математики в мире, высказывать хорошо обоснованные суждения и принимать решения, которые необходимы конструктивному, активному и размышляющему гражданину.
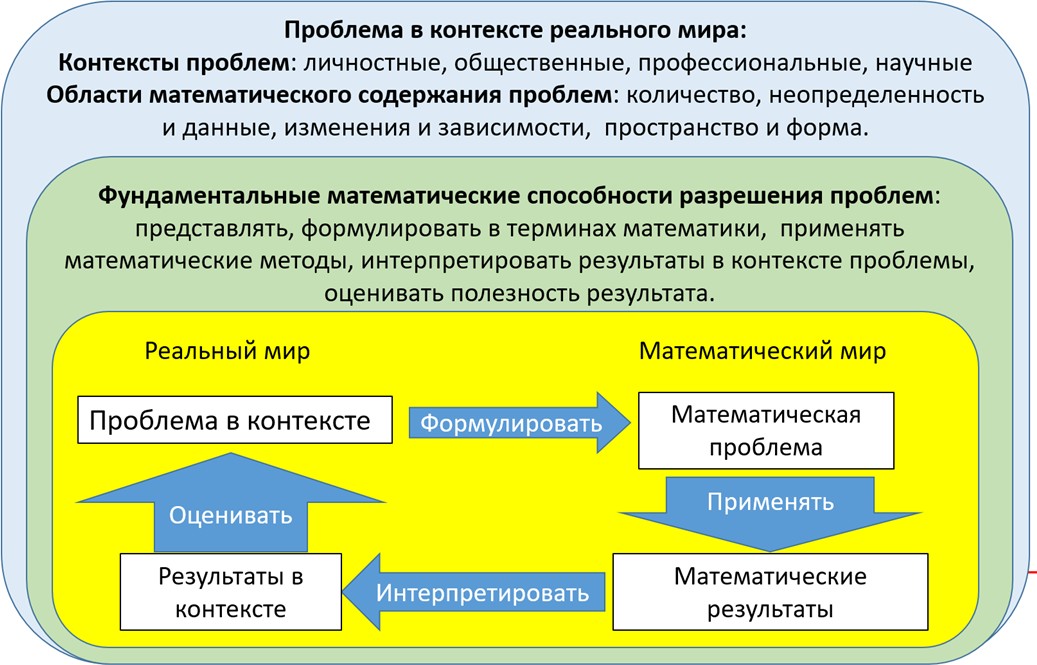Структура математической грамотности
Межпредметность и метапредметность математической грамотности
Межпредметность математической грамотности включает в себя - мотивацию, применение, объяснение, демонстрацию.
Математическая грамотность позволяет
решать учебно-познавательные и учебно-практические задачи, требующие полного и критического понимания текста;
удерживать условия задания в процессе решения;
самоконтроль за выполнением условий (ограничений) в описании ситуации при нахождении решения и интерпретации полученного решения в рамках предложенной ситуации;
работать с информацией, представленной в различной форме (текста, таблицы, диаграммы столбчатой или круговой, схемы, рисунка, чертежа с обозначением видимых и невидимых элементов геометрической фигуры) в контексте конкретной проблемы.
Уровни математической грамотности
Давайте разберем несколько задач и ответим на поставленные вопросы.
Задача №1
Ответим на вопросы:
1.виды математической деятельности? 2. уровень математической грамотности?
3. контекст проблемы? 4.область математического содержания проблемы 5.фундаментальные математические способности разрешения проблемы Ученик хочет изобразить эти данные на столбчатой диаграмме. Приведите одну причину, по которой столбчатая диаграмма не подходит для изображения этих данных.
ОЦЕНКА ВЫПОЛНЕНИЯ:
Ответ принимается полностью (трудность – 551) – 1 балл.
Процент учащихся, набравших данный балл: 31,8 - Россия; 51,5 - средний по ОЭСР; 74,8 - Корея (максимальный).
Код 1А: Причина сфокусирована на большом различии между данными для некоторых видов мусора.
Ответ № 1: «Различие в высоте столбцов на столбчатой диаграмме будет слишком большим».
Ответ № 2: «Если взять столбик в 10 см для полистирола, то столбик для картонных коробок будет высотой 0,05 см».
Код 1 В: Причина сфокусирована на неопределенности данных для некоторых видов мусора.
Ответ № 3: «Высота столбика для «полистироловых чашек» неопределимая».
Ответ № 4: «Вы не построите один столбик для данных 1-3 года или один столбик для данных 20-25 лет».
Ответ не принимается:
Код 0: Другие ответы.
№ 5: Потому что она не годится.№ 6: Пиктограмма лучше.
№ 7: Вы не можете проверить эту информацию
№ 8: Потому что числа, указанные в таблице, приближенные. Код 9: Ответ отсутствует.
ОТВЕТЫ НА ВОПРОСЫ
исследовательская
Задание проверяет: 3-ий уровень компетентности – рассуждения (широкий спектр математических рассуждений)
контекст проблемы, ситуация: научная
Область математического содержания: неопределенность 5 интерпретировать результаты в контексте проблемы
Анализ понятий «разложение» и «время, необходимое для разложения бытовых отходов». В тексте задания не объяснено, что значит понятие «разложение», что значит «время разложения», не объяснено, почему имеется большой разброс по времени разложения для одного вида отходов, почему полистирол более устойчив, чем бумага и т.п. Не понимая всего этого, учащиеся вынуждены отвечать вопрос: «Можно ли для отображения этих данных использовать столбчатую диаграмму?». Имеет смысл разъяснить читателю эти понятия. Например, в случае бумаги конечными продуктами разложения являются: перегной, тела различных микроорганизмов, углекислый газ, метан и вода. Большой разброс данных по времени разложения бумаги в естественных условиях: от месяца до 10 лет объясняется тем, что не указаны условия, при которых происходит разложение. Бумага состоит в основном из клетчатки (целлюлозы). Разложение клетчатки происходит под действием микроорганизмов. Активность микроорганизмов зависит от многих условий, в том числе и от температуры. Например, в Антарктиде газетная бумага будет сохраняться, наверное, в течение столетий, а в тропиках разложение произойдет в течение нескольких месяцев.
Целлюлозоразлагающие микроорганизмы выполняют огромную санитарную роль, разлагая в аэробных и анаэробных условиях клетчатку отмерших растений, благодаря чему в почве накапливается гумус (перегной), повышающий ее плодородие. Почему для разложения полистирола необходимо более ста лет? Потому что он химически устойчив, и микроорганизмы его не «едят». Под действием ультрафиолета (часть солнечного излучения) он очень медленно окисляется кислородом воздуха. Клетчатка тоже химически устойчива, но ее «едят» микроорганизмы.
Задача №2
Задание «ПИЦЦА» В пиццерии продаются два вида круглой пиццы, имеющих одинаковую толщину и разные размеры. Диаметр меньшей пиццы равен 30 см, и она стоит 30 зедов. Диаметр большей пиццы равен 40 см, и она стоит 40 зедов. Какие пиццы выгоднее продавать хозяину пиццерии? Приведите ваши рассуждения.
Сравним площадь этих пицц. S кр.=1/4 * π * D²
S1=1/4 * π * 900 ≈ 706,5 см² S2=1/4 * π * 1600 ≈ 1256 см²
Стоимость 1 см² первой пиццы≈15 : 706,5≈0,021 зеда. Стоимость 1 см² второй пиццы ≈25 : 1256≈0,019 зеда. Вывод: Выгоднее покупать большую.
Ответим на вопросы:
виды математической деятельности? (познавательная)
уровень математической грамотности? (5 создают сложные математические модели для решения проблемы, оценивают стратегию)
контекст проблемы? (личностный (профессиональные)
область математического содержания проблемы (изменения и зависимость) 5.фундаментальные математические способности разрешения проблемы (формулировать в терминах математики , т к требуется создать модель решения) Решение:
Sменьшей пиццы= 3,14(30:2)2= 706,5 (см2) Sбольшей пиццы= 3,14(40:2)2= 1256 (см2) 1 см2меньшей пиццы будет стоить 30 : 706,5 ≈ 0,042 (зед.) 1 см2большей пиццы
будет стоить 40 : 1256 ≈ 0,032 (зед.) на 1 зед можно купить 706,5:30= 23,55 (см2) меньшей пиццы на 1 зед можно купить 1256 :40 = 31,4 (см2) большей пиццы большая пицца выгоднее покупателю, а меньшая – продавцу При втором подходе нужно поделить площадь пиццы на её стоимость. S меньшей пиццы = 3,14 (30:2)2= 706,5 (см2); на 1 зед можно купить 706,5:30= 23,55 (см2) Sбольшей пиццы = 3,14 (40:2)2 =
1256 (см2); на 1 зед можно купить 1256 :40 = 31,4 (см2)
Полученное решение показало, что хозяину выгоднее продавать меньшие пиццы, так как на 1 зед покупатель может купить меньшую площадь у меньшей пиццы и большую площадь у большей пиццы. То есть большая пицца выгоднее покупателю, а меньшая – продавцу.
ВЫВОД Задание оказалось одним из самых трудных, в 2003 г. с ним справилось всего 11% из всех участников исследования. Ключевым моментом для решения задачи является установление зависимости между размером пиццы и её стоимостью, поэтому задание отнесено к области «Изменение и зависимости». Сам контекст носит личностный характер. По характеру превалирующей познавательной деятельности задание отнесено к когнитивной области «Формулировать», так как требуется создать модель решения задачи.
Подведем итог Чему мы учим учеников на уроках математики?
1
