
ГАПОУ КО «ККЭТ»
Студентка группы Д-21
Шадрина Екатерина
Тела вращения

«Знаете ли Вы, что…»
В далеком прошлом, важнейшей задачей египетской и вавилонской геометрии было определение объема различных пространственных тел. Эта задача отвечала необходимости строить дома, дворцы, храмы и другие сооружения. Объемы сооружений в виде кубов, призм и цилиндров египтяне и вавилоняне, китайцы и индийцы вычисляли путем умножения площади основания на высоту. Однако древнему Востоку были известны в основном только отдельные правила, найденные опытным путем. В более позднее время, когда геометрия сформировалась как наука, был найден общий подход к вычислению площадей и объемов многогранников и тел вращения. Среди замечательных греческих ученых V-IV вв. до н.э., которые разрабатывали теорию объемов, были :
Евклид
Архимед
Демокрит
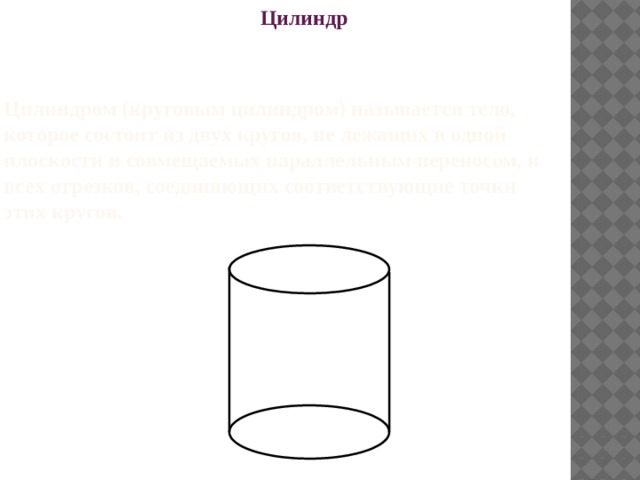
Цилиндр
Цилиндром (круговым цилиндром) называется тело, которое состоит из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.
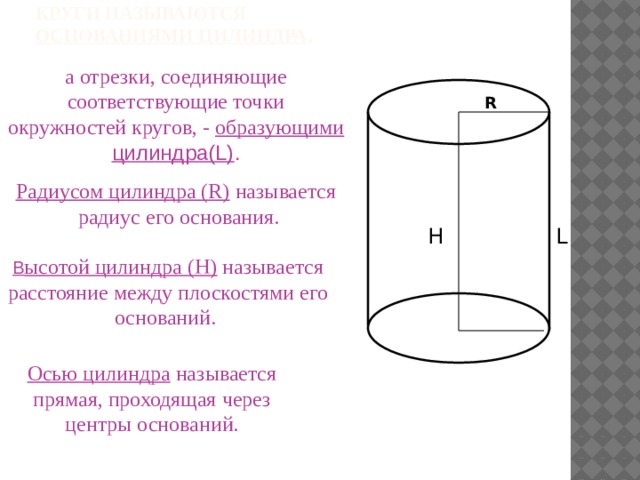
Круги называются основаниями цилиндра ,
а отрезки, соединяющие соответствующие точки окружностей кругов, - образующими цилиндра(L) .
R
Радиусом цилиндра (R) называется радиус его основания.
H
L
В ысотой цилиндра (H) называется расстояние между плоскостями его оснований.
Осью цилиндра называется прямая, проходящая через центры оснований.
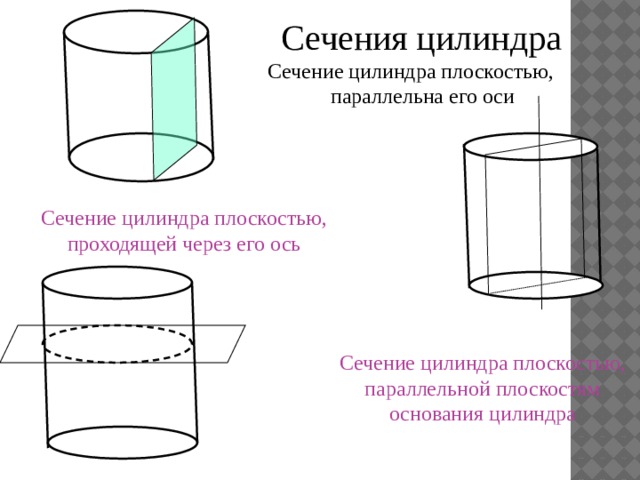
Сечения цилиндра
Сечение цилиндра плоскостью, параллельна его оси
Сечение цилиндра плоскостью, проходящей через его ось
Сечение цилиндра плоскостью, параллельной плоскостям основания цилиндра

Основные формулы:
1. Объем цилиндра равен произведению площади основания на высоту.
2. Площадь боковой поверхности цилиндра вычисляется по формуле
3. Площадь полной поверхности цилиндра вычисляется по формуле
где R – радиус цилиндра, H – высота, L - образующая

Конус
Конусом (круговым конусом) называется тело, которое состоит из круга – основания конуса, точки, не лежащей в плоскости этого круга, - вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания.
H
L
R

Конус называется прямым , если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания.
Высотой конуса (H) называется перпендикуляр, опущенный из его вершины на плоскость основания. У прямого конуса основание высоты совпадает с центром основания.
H
L
Осью прямого кругового конуса называется прямая, содержащая его высоту.
R
Образующая конуса L отрезок соединяющий вершину конуса с точкой окружности основания.
R-радиус основания конуса
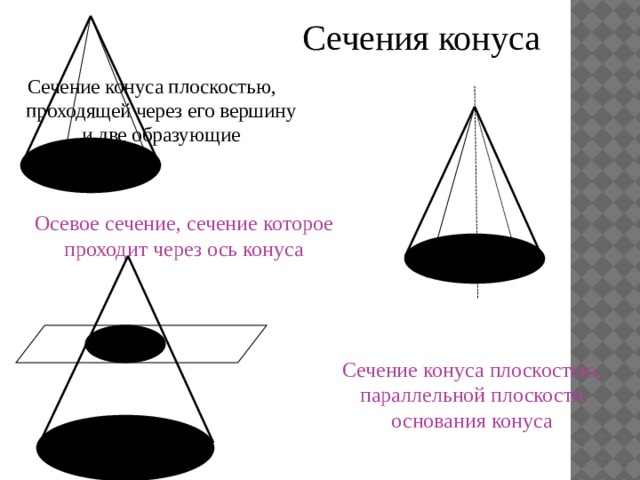
Сечения конуса
Сечение конуса плоскостью, проходящей через его вершину и две образующие
Осевое сечение, сечение которое проходит через ось конуса
Сечение конуса плоскостью, параллельной плоскости основания конуса

Основные формулы
1. Объем конуса равен
2. Площадь основания равна.
3. Площадь боковой поверхности прямого конуса равна
4. Площадь полной поверхности конуса равна
Н-высота конуса, R-радиус основания, L - образующая

Усеченный конус
Плоскость, параллельная основанию конуса и пересекающая конус, отсекает от него меньший конус. Оставшаяся часть называется усеченным конусом .

Круги называются основаниями усеченного конуса ,
а отрезки, соединяющие соответствующие точки окружностей кругов, - образующими (L)усеченного конуса .
R 2
R 1 R 2 – радиусы оснований усеченного конуса
L
H
Высотой (H) усеченного конуса называется расстояние между плоскостями его оснований.
R 1
Осью усеченного конуса называется прямая, проходящая через центры оснований.
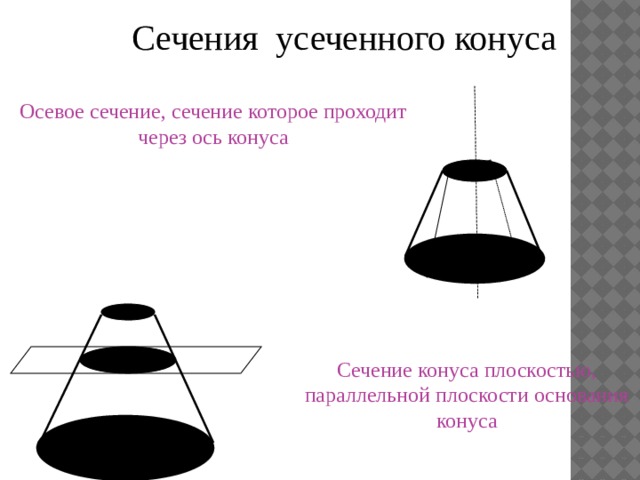
Сечения усеченного конуса
Осевое сечение, сечение которое проходит через ось конуса
Сечение конуса плоскостью, параллельной плоскости основания конуса

Основные формулы:
1. Объем усеченного конуса равен
2. Площадь боковой поверхности усеченного конуса
(Для вычисления площади оснований используется формула площади круга)
3. Площадь полной поверхности усеченного конуса
где, радиусы оснований R 1 и R 2 , образующая L, высота H

Ш а р
Шаром называется тело, которое состоит из точек пространства, находящихся на расстоянии, не большем данного, от данной точки. Эта точка называется центром шара, а данное расстояние радиусом шара.
О
R
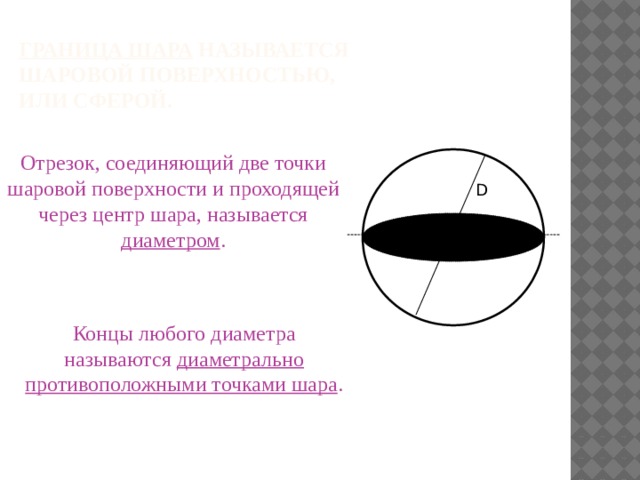
Граница шара называется шаровой поверхностью, или сферой.
Отрезок, соединяющий две точки шаровой поверхности и проходящей через центр шара, называется диаметром .
D
О
Концы любого диаметра называются диаметрально противоположными точками шара .
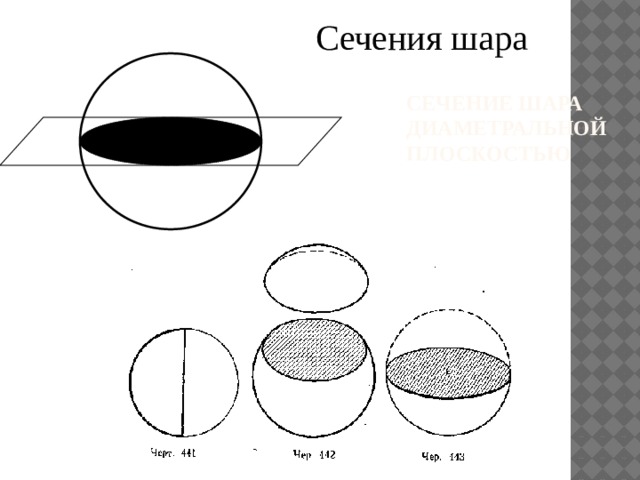
Сечения шара
Сечение шара диаметральной плоскостью
О
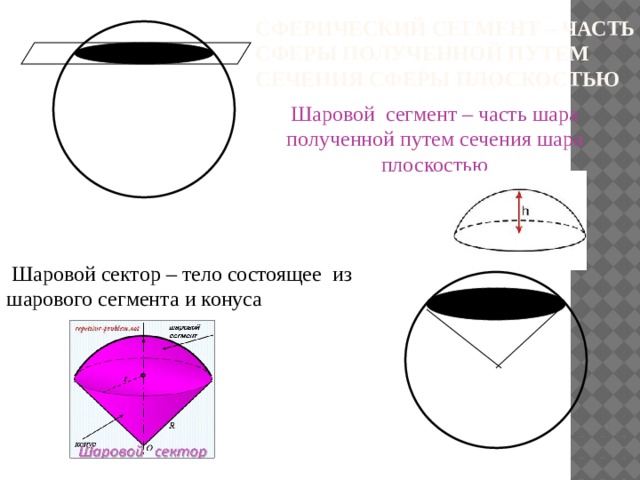
Сферический сегмент – часть сферы полученной путем сечения сферы плоскостью
О
Шаровой сегмент – часть шара полученной путем сечения шара плоскостью
Шаровой сектор – тело состоящее из шарового сегмента и конуса
О

Основные формулы:
1 . Площадь сферы радиуса R вычисляется по формуле
2. Объем шара определяется по формуле
R
3. Объем шарового сектора определяется по формуле, где R – радиус шара, H – высота соответствующего шарового фрагмента.
4. Площадь сферического сегмента вычисляется по формуле, где H – высота сегмента





