
Алгебра логики
Логические элементы

Логика - это наука о формах и способах мышления.
- Алгебра логики – математический аппарат, с помощью которого записывают (кодируют), упрощают, вычисляют и преобразовывают логические высказывания.
- Высказывание -это повествовательное предложение, о котором можно сказать, истинно оно или ложно.
- Высказывание может принимать только одно из двух логических значений - истинно или ложно .

В алгебре высказываний высказывания обозначаются именами логических переменных, которые могут принимать лишь два значения « истинно » и « ложно ».
Истинно =1 Ложно=0
Примеры высказываний :
- Земля – планета Солнечной системы ( истинное высказывание ).
- 3+6 10 ( ложное высказывание ).

Задание
- Объясните, почему следующие предложения не являются высказываниями:
А) Уходя гасите свет.
Б) Какого цвета этот дом?
В) Посмотрите в окно.

Самостоятельное задание
- Придумайте несколько высказываний:
А)
Б)
В)

Самостоятельное задание
- Придумайте 2-3 предложения, которые не являются высказываниями:
А)
Б)
В)

Высказывания бывают простые и сложные
Простое высказывание (логическая переменная ) содержит только одну простую мысль. Логические переменные обычно обозначаются буквами латинского алфавита: A, B, C, D…
Например , А = {Квадрат – это ромб}.
Сложное высказывание (логическая функция ) содержит несколько простых мыслей, соединенных между собой с помощью логических операций.
Например ,
F(A,B) - {Лил дождь, и дул холодный ветер}
А В
- А В
- А В
- А В
- А В

Значение логической функции можно определить с помощью специальной таблицы - (таблицы истинности)
- Таблица истинности — это таблица, в которой перечислены все возможные значения входящих логических переменных и соответствующие им значения функции.

Например,
А
В
0
0
F (А,В)
0
1
0
1
1
0
1
1
0
0
А и В – логические переменные, n =2
F – логическая функция
Количество строк ( q ) в таблице истинности можно вычислить по формуле q=2 n .

Согласно определению, таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы.
Для формулы, которая содержит две переменные, таких наборов значений переменных всего четыре:
(0, 0), (0, 1), (1, 0), (1, 1).

Для образования новых высказываний используются базовые логические операции:
- логическое отрицание -операция «не» - инверсия
- логическое умножение - операция «и» - конъюнкция
- логическое сложение - операция «или» - дизъюнкция
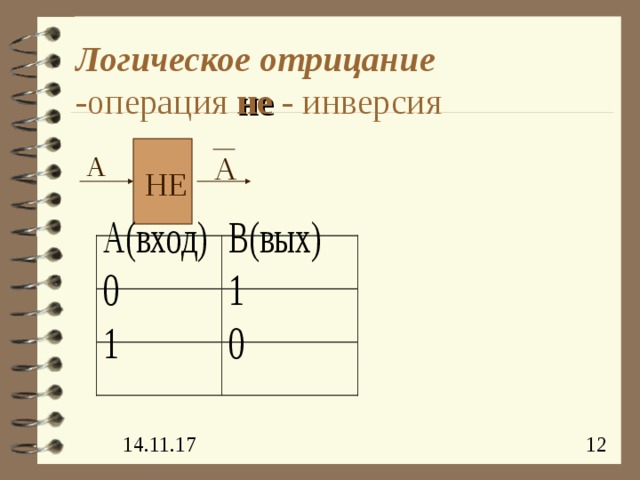
Логическое отрицание -операция не - инверсия
А
А
НЕ

Логическое умножение - операция и - конъюнкция
А
C=A&B
С
И
В
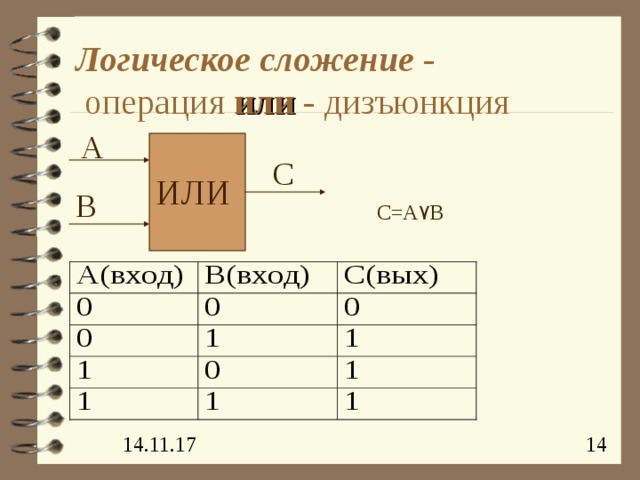
Логическое сложение - операция или - дизъюнкция
А
С
ИЛИ
В
C=A ۷ B
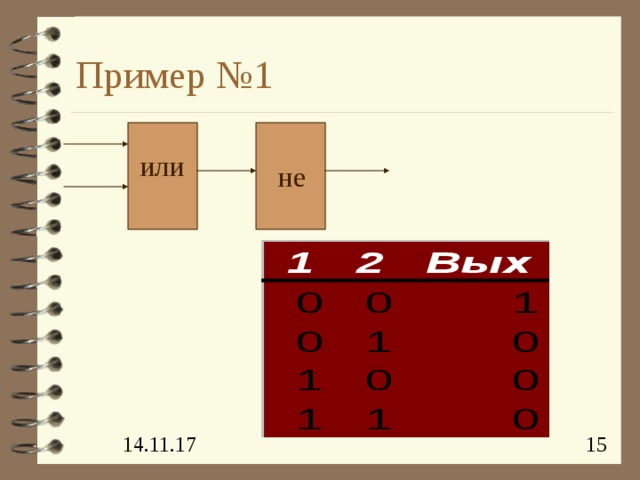
Пример №1
или
не
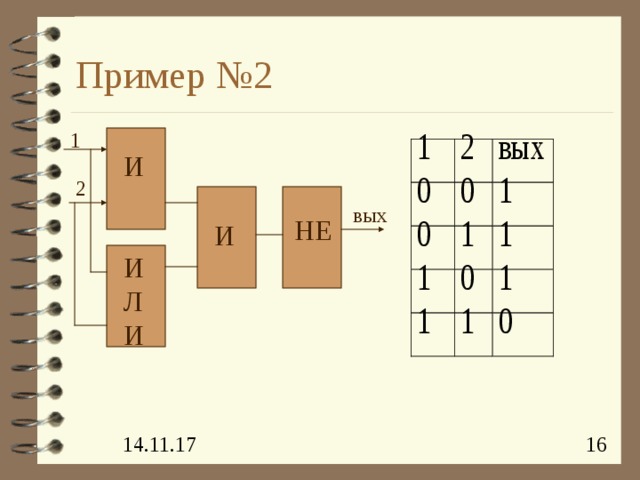
Пример №2
1
И
2
вых
НЕ
И
ИЛИ
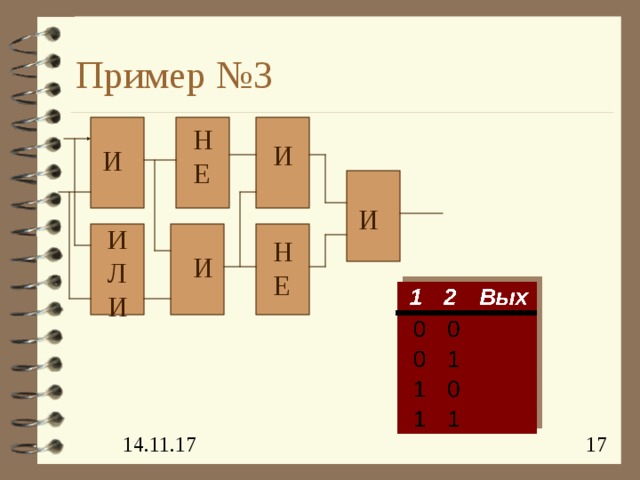
Пример №3
НЕ
И
И
И
И ЛИ
НЕ
И
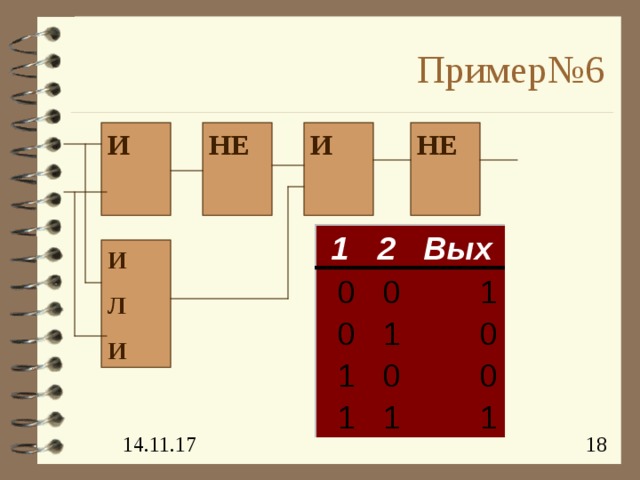
Пример№6
НЕ
НЕ
И
И
И
Л
И
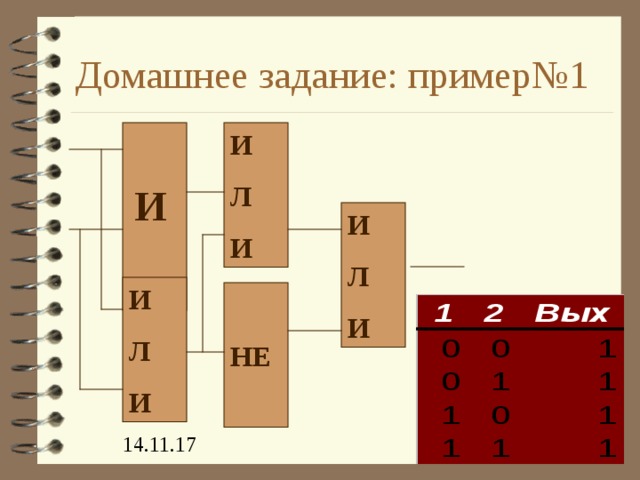
Домашнее задание: пример№1
И
И
Л
И
И
Л
И
И
Л
И
НЕ
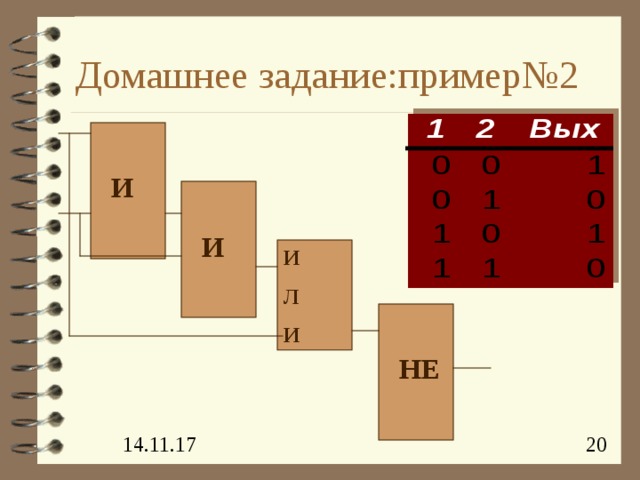
Домашнее задание:пример№2
И
И
И
Л
И
НЕ
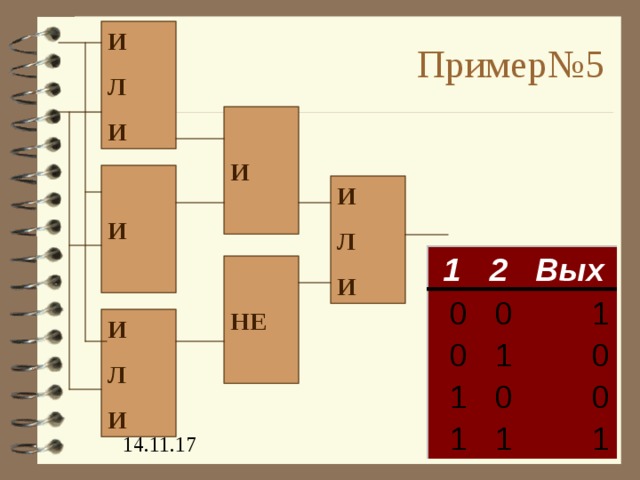
Пример№5
И
Л
И
И
И
И
Л
И
НЕ
И
Л
И
И
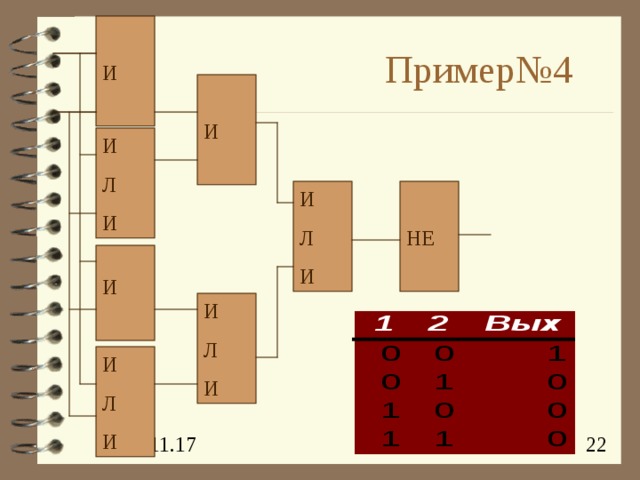
Пример№4
И
И
Л
И
НЕ
И
Л
И
И
И
Л
И
И
Л
И
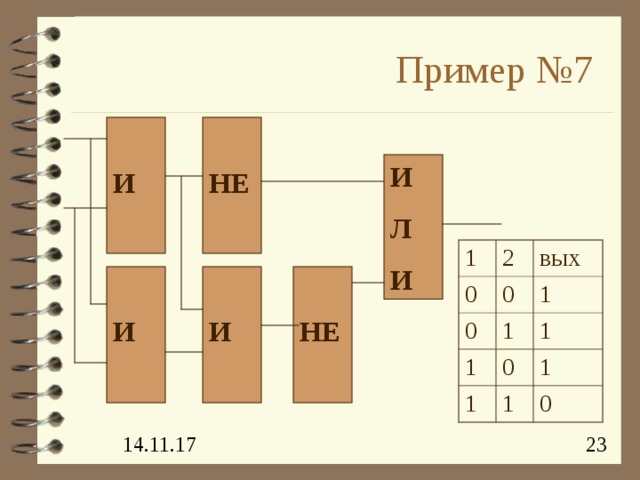
Пример №7
И
НЕ
И
Л
И
1
0
2
0
0
вых
1
1
1
1
1
0
1
1
0
И
И
НЕ
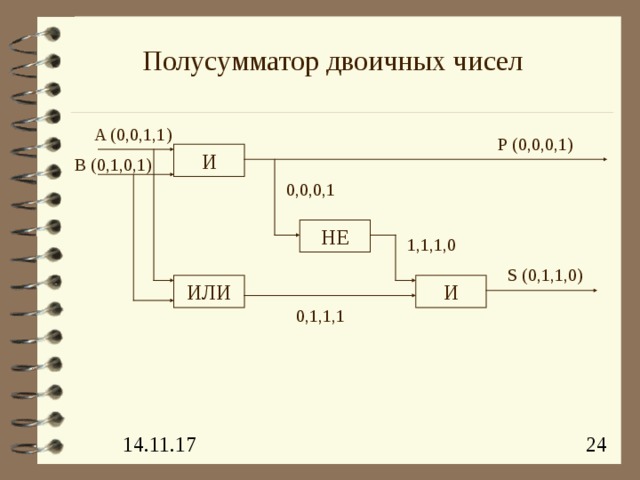
Полусумматор двоичных чисел
A (0,0,1,1)
Р (0,0,0,1)
И
B (0,1,0,1)
0,0,0,1
НЕ
1,1,1,0
S (0,1,1,0)
ИЛИ
И
0,1,1,1

Пример№8
F(A,B,C)=(A^B) ۷ (A ۷ C)
=(A*B)+(A+C)
۷ C

Пример№8
F(A,B,C)=(A^B) ۷ (A ۷ C)
=(A*B)+(A+C)
۷ C

Пример№8
F(A,B,C)=(A^B) ۷ (A ۷ C)
=(A*B)+(A+C)
۷ C

Пример№8
F(A,B,C)=(A^B) ۷ (A ۷ C)
=(A*B)+(A+C)
۷ C

Пример№8
F(A,B,C)=(A^B) ۷ (A ۷ C)
=(A*B)+(A+C)
۷ C
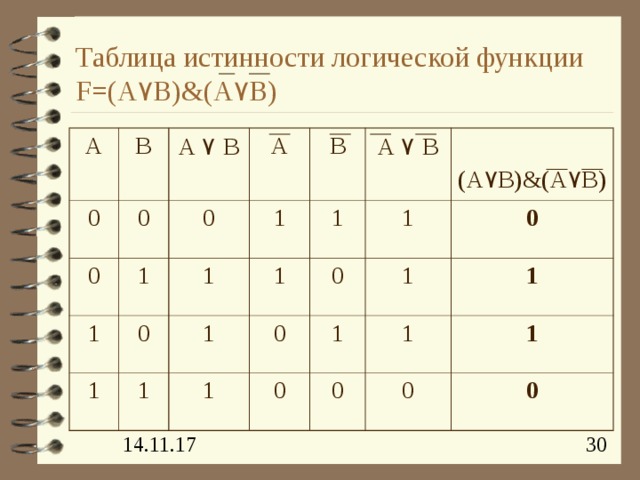
Таблица истинности логической функции F=(A ۷ B)&(A ۷ B)
A
B
0
0
0
A ۷ B
1
A
1
0
1
1
B
1
0
1
A ۷ B
1
1
1
1
(A ۷ B)&(A ۷ B)
0
0
1
0
1
1
0
1
0
1
0
1
0
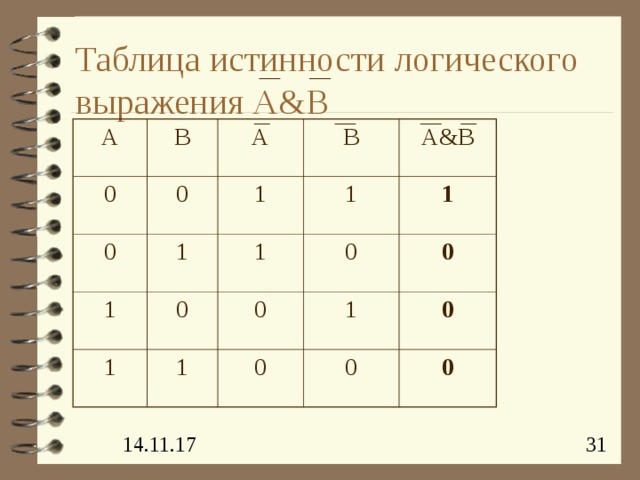
Таблица истинности логического выражения A&B
A
B
0
0
0
A
1
B
1
1
A&B
1
0
1
1
1
0
0
1
1
0
0
0
0
0
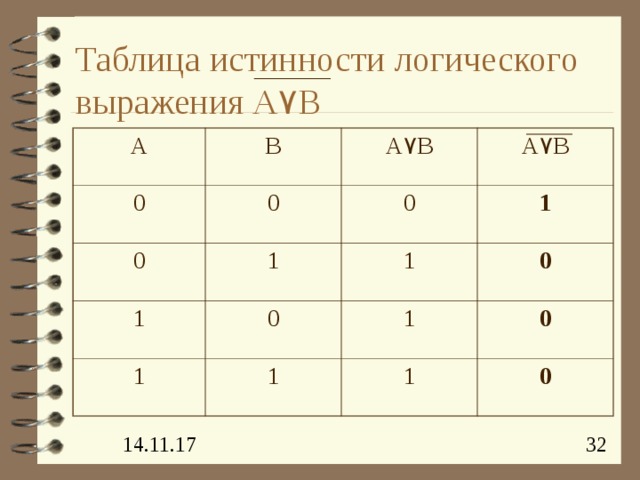
Таблица истинности логического выражения A ۷ B
A
B
0
0
0
A ۷ B
1
1
0
A ۷ B
1
0
1
1
1
1
0
0
1
0

Логические законы и правила преобразования логических выражений
- Закон тождества : всякое высказывание тождественно самому себе.
А=А
- Закон непротиворечия: высказывание не может быть одновременно истинным и ложным.
А & А=1
- Закон исключенного третьего. Высказывание может быть истинным, либо ложным, третьего не дано.
А ۷ А=1
- Закон двойного отрицания: если дважды отрицать некоторое высказывание, то в результате мы получим исходное высказывание.
А=А

Логические законы и правила преобразования логических выражений
- Законы Моргана:
А ۷ В=А & В
А & В=А ۷ В

- Таблицы истинности совпадают, следовательно, логические выражения равносильны: A&B = A&B
- Докажите , используя таблицы истинности, что логические выражения А ۷ В и А & В равносильны

Домашнее задание
- Докажите справедливость первого закона Моргана , используя таблицы истинности.
- Докажите справедливость второго закона Моргана , используя таблицы истинности.
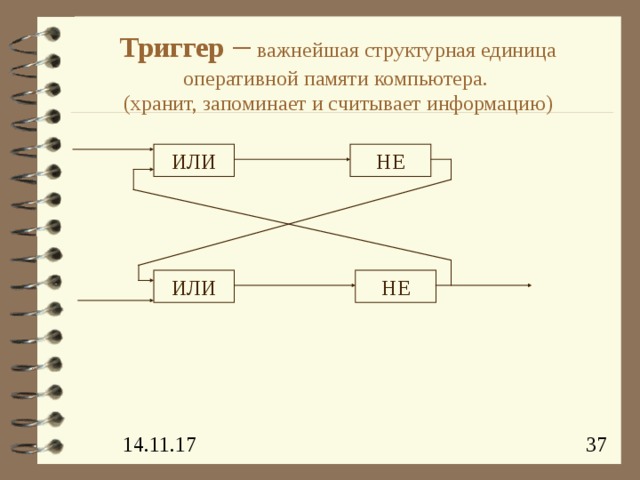
Триггер – важнейшая структурная единица оперативной памяти компьютера. (хранит, запоминает и считывает информацию)
ИЛИ
НЕ
НЕ
ИЛИ





