Тема урока: Практическое применение тригонометрии».
Класс: 10
Тип урока: урок обобщения.
Цель урока: показать значимость и практическое применение знаний тригонометрии в жизни человека.
Задачи:
Повторение истории возникновения тригонометрии и свойств тригонометрических функций.
Развитие познавательного интереса и привитие стремления к изучению предмета математики.
Воспитание творчества, самостоятельности и работы в группах.
Ход урока
Наука тригонометрия возникла и развивалась в древности как один из разделов астрономии, как её вычислительный аппарат, отвечающий практическим нуждам человека.
Некоторые тригонометрические сведения были известны древним вавилонянам и египтянам, но основы этой науки заложены в Древней Греции.
Греческий астроном Гиппарх во II в. до н. э. составил таблицу числовых значений хорд в зависимости от величин стягиваемых ими дуг. Более полные сведения из тригонометрии содержатся в известном “Альмагесте” Птолемея. Сделанные расчёты позволили Птолемею составить таблицу, которая содержала хорды от 0 до 180 ![]() .
.
Название линий синуса и косинуса впервые были введены индийскими учёными. Они же составили первые таблицы синусов, хотя и менее точные, чем птолемеевы.
В Индии начинается по существу учение о тригонометрических величинах, названное позже гониометрией (от “гониа” - угол и “метрио” - измеряю).
На пороге XVII в. в развитии тригонометрии начинается новое направление – аналитическое.
Тригонометрия даёт необходимый метод развития многих понятий и методы решения реальных задач, возникающих в физике, механике, астрономии, геодозии, картографии и других науках. Кроме этого, тригонометрия является большим помощником в решении стереометрических задач.
Почему на инженерном микрокалькуляторе, имеющем клавиши для вычисления синуса, косинуса и тангенса угла, нет клавиши для вычисления котангенса?
Ответ: такой калькулятор оснащен клавишей для вычисления числа, обратного
Один из семи мудрецов Древней Греции Фалес Милетский вычислил высоту одной из египетских пирамид. Он утверждал, что «когда тень от меня будет равна моему росту, то тень от пирамиды будет равна высоте пирамиды». Какое свойство котангенса использовал Фалес?
Ответ: котангенс угла зависит только от величины угла и не зависит от размеров и расположения треугольника
Многие задаются вопросами:
зачем нужна тригонометрия?
Как она используется в нашем мире?
С чем может быть связана тригонометрия?
И вот ответы на эти вопросы.
Тригонометрия или тригонометрические функции используются в астрономии (особенно для расчётов положения небесных объектов), когда требуется сферическая тригонометрия, в морской и воздушной навигации, в теории музыки, в акустике, в оптике, в анализе финансовых рынков, в электронике, в теории вероятности, в статистике, в биологии, в медицинской визуализации ,например, компьютерной томографии и ультразвук, в аптеках, в химии, в теории чисел, в сейсмологии, в метеорологии, в океанографии, во многих физических науках, в межевании и геодезии, в архитектуре, в фонетике, в экономике, в электротехнике, в машиностроении, в гражданском строительстве, в компьютерной графике, в картографии, в кристаллографии, в разработке игр и многих других областях.
Геодезия
Часто с синусами и косинусами приходится сталкиваться геодезистам. Они имеют специальные инструменты для точного измерения углов. При помощи синусов и косинусов углы можно превратить в длины или координаты точек на земной поверхности.
Древняя астрономия
Зачатки тригонометрии можно найти в математических рукописях Древнего Египта, Вавилона и Древнего Китая. 56-я задача из папируса Ринда (II тысячелетие до н. э.) предлагает найти наклон пирамиды, высота которой равна 250 локтей, а длина стороны основания — 360 локтей.
Дальнейшее развитие тригонометрии связано с именем астронома Аристарха Самосского (III век до н. э.). В его трактате «О величинах и расстояниях Солнца и Луны» ставилась задача об определении расстояний до небесных тел; эта задача требовала вычисления отношения сторон прямоугольного треугольника при известном значении одного из углов. Аристарх рассматривал прямоугольный треугольник, образованный Солнцем, Луной и Землёй во время квадратуры. Ему требовалось вычислить величину гипотенузы (расстояние от Земли до Солнца) через катет (расстояние от Земли до Луны) при известном значении прилежащего угла (87°), что эквивалентно вычислению значения sin угла 3. По оценке Аристарха, эта величина лежит в промежутке от 1/20 до 1/18, то есть расстояние до Солнца в 20 раз больше, чем до Луны; на самом деле Солнце почти в 400 раз дальше, чем Луна, ошибка возникла из-за неточности в измерении угла.
Несколько десятилетий спустя Клавдий Птоломей в своих трудах «География», «Аналемма» и «Планисферий» даёт подробное изложение тригонометрических приложений к картографии, астрономии и механике. Среди прочего, описана стереографическая проекция, исследованы несколько практических задач, например: определить высоту и азимут небесного светила по его склонению и часовому углу. С точки зрения тригонометрии, это значит, что надо найти сторону сферического треугольника по другим двум сторонам и противолежащему углу.
В общем, можно сказать, что тригонометрия использовалась для:
точного определения времени суток;
вычисления будущего расположения небесных светил, моментов их восхода и заката, затмений Солнца и Луны;
нахождения географических координат текущего места;
вычисления расстояния между городами с известными географическими координатами.
Гномон - древнейший астрономический инструмент, вертикальный предмет (стела, колонна, шест), позволяющий по наименьшей длине его тени (в полдень) определить угловую высоту солнца.
Так, под котангенсом понималась длина тени от вертикального гномонавысотой 12 (иногда 7) единиц; первоначально эти понятия использовались для расчёта солнечных часов. Тангенсом называлась тень от горизонтального гномона. Косекансом и секансом назывались гипотенузы соответствующих прямоугольных треугольников (отрезки AO на рисунке слева)
Архитектура
Широко используется тригонометрия в строительстве, а особенно в архитектуре. Большинство композиционных решений и построений рисунков проходило именно с помощью геометрии. Но теоретические данные мало что значат. Хочу привести пример на построение одной скульптуры французского мастера Золотого века искусства.
Пропорциональное соотношение в построении статуи было идеально. Однако при поднятии статуи на высокий пьедестал, она смотрелась уродливой. Скульптором не было учтено, что в перспективе к горизонту уменьшаются многие детали и при взгляде снизу вверх уже не создается впечатления ее идеальности. Велось множество расчетов, чтобы фигура с большой высоты смотрелась пропорционально. В основном они были основаны на методе визирования, то есть приблизительного измерения, на глаз. Однако коэффициент разности тех или иных пропорций позволили сделать фигуру более приближенной к идеалу. Таким образом, зная примерное расстояние от статуи до точки зрения, а именно от верха статуи до глаз человека и высоту статуи, можно рассчитать синус угла падения взгляда с помощью таблицы (тоже самое мы можем сделать и с нижней точкой зрения), тем самым найдем точку зрения
Ситуация меняется , так как статую поднимают на высоту, поэтому расстояние от верхушки статуи до глаз человека увеличивается, следовательно и синус угла падения увеличивается. Сравнив изменения расстояния от верхушки статуи до земли в первом и во втором случаи, можно найти коэффициент пропорциональности. Впоследствии мы получим чертеж, а потом скульптуру, при поднятии которой зрительно фигура будет приближена к идеалу
Медицина и биология
Модель боритмов можно построить с помощью тригонометрических функций. Для построения модели биоритмов необходимо ввести дату рождения человека, дату отсчета (день, месяц, год) и длительность прогноза (кол-во дней).
Формула сердца. В результате исследования, проведенного студентом иранского университета Шираз Вахидом-Резой Аббаси, медики впервые получили возможность упорядочить информацию, относящуюся к электрической активности сердца или, другими словами, электрокардиографии. Формула представляет собой комплексное алгебраически-тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчетов в случаях аритмии. Как утверждают медики, эта формула в значительной степени облегчает процесс описания основных параметров деятельности сердца, ускоряя, тем самым, постановку диагноза и начало собственно лечения.
Также тригонометрия помогает нашему мозгу определять расстояния до объектов.
Американские ученые утверждают, что мозг оценивает расстояние до объектов, измеряя угол между плоскостью земли и плоскостью зрения. Строго говоря, идея "измерения углов" не является новой. Еще художники Древнего Китая рисовали удаленные объекты выше в поле зрения, несколько пренебрегая законами перспективы. Сформулировал теорию определения расстояния по оценке углов арабский ученый XI века Альхазен. После долгого забвения в середине прошлого столетия идею реанимировал психолог Джеймс Гибсон (James Gibson), строивший свои выводы на основе опыта работы с пилотами военной авиации. Однако после того о теории вновь позабыли.
Движение рыб в воде происходит по закону синуса или косинуса, если зафиксировать точку на хвосте, а потом рассмотреть траекторию движения. При плавании тело рыбы принимает форму кривой, которая напоминает график функции y=tgx.
Измерительные работы
Тригонометрией пользуются при измерение расстояния между точек на местности. Предположим, что нам надо найти расстояние d от пункта А до недоступного пункта «дерево». На местности можно выбрать точку d B и измерим длину с отрезка АВ. Затем измерим, например с помощью астролябии, углы A и B. Эти данные, т.е. c, a и b позволяют решить треугольник АВС и найти искомое расстояние d=AC. Сначала находим угол С sinC:
С=180-а-b, sinC=sin(180-a-b)=sin(a+b)
Затем с помощью теоремы синусов находим d.
Тригонометрия в физике
В окружающем нас мире приходится сталкиваться с периодическими процессами, которые повторяются через одинаковые промежутки времени. Эти процессы называются колебательными. Колебательные явления различной физической природы подчиняются общим закономерностям и описываются одинаковыми уравнениями. Существуют разные виды колебательных явлений.
Гармоническое колебание - явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса. Например, гармонически колеблется величина, изменяющаяся во времени.
Механические колебания
Механическими колебаниями называют движения тел, повторяющиеся точно через одинаковые промежутки времени. Графическое изображение этой функции дает наглядное представление о протекании колебательного процесса во времени. Примерами простых механических колебательных систем могут служить груз на пружине или математический маятник.
Тригонометрия в природе
Мы часто задаем вопрос «Почему мы иногда видим то, чего нет на самом деле?». Для исследования предложены следующие вопросы: «Как возникает радуга? Северное сияние?», «Что такое оптические иллюзии?» , «Как тригонометрия может помочь найти ответы на эти вопросы?».
Впервые теория радуги была дана в 1637 году Рене Декартом. Он объяснил радугу, как явление, связанное с отражением и преломлением света в дождевых каплях.
Северное сияние Проникновение в верхние слои атмосферы планет заряженных частиц солнечного ветра определяется взаимодействием магнитного поля планеты с солнечным ветром.
Сила, действующая на движущуюся в магнитном поле заряженную частицу называется силой Лоренца. Она пропорциональна заряду частицы и векторному произведению поля и скорости движения частицы.
Многофункциональная тригонометрия
Американские ученые утверждают, что мозг оценивает расстояние до объектов, измеряя угол между плоскостью земли и плоскостью зрения.
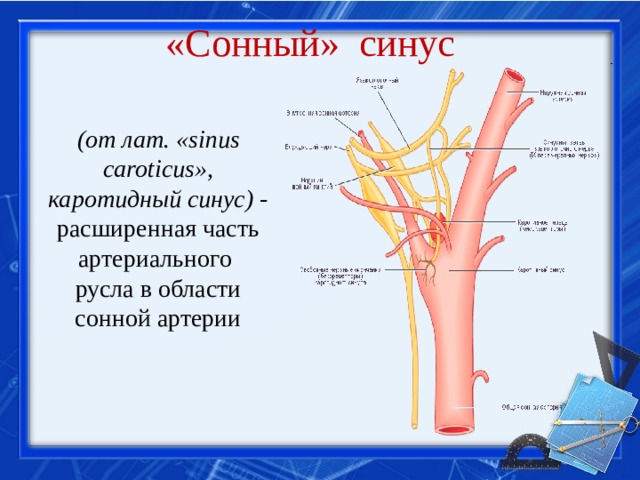
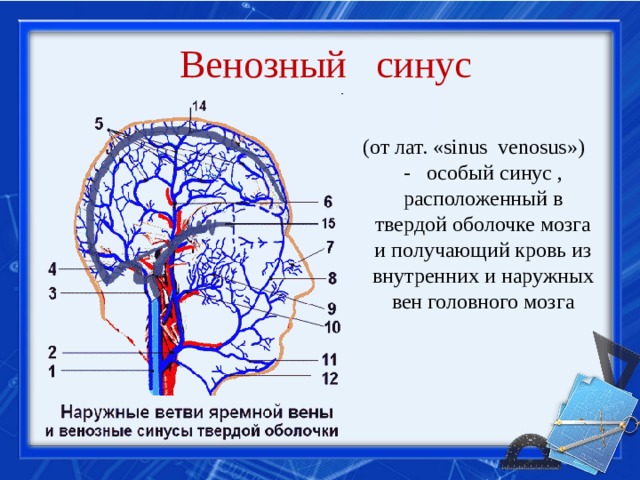
К тому же в биологии используется такое понятие как синус сонный, синус каротидный и венозный или пещеристый синус.
Тригонометрия играет важную роль в медицине. С ее помощью иранские ученые открыли формулу сердца - комплексное алгебраически-тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчетов в случаях аритмии.
Тригонометрия и тригонометрические функции в медицине и биологии.
Одно из фундаментальных свойств живой природы - это цикличность большинства происходящих в ней процессов.
Биологические ритмы, биоритмы – это более или менее регулярные изменения характера и интенсивности биологических процессов.
Основной земной ритм – суточный.
Модель биоритмов можно построить с помощью тригонометрических функций.
Тригонометрия в биологии
Какие биологические процессы связаны с тригонометрией?
Тригонометрия играет важную роль в медицине. С ее помощью иранские ученые открыли формулу сердца - комплексное алгебраически-тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчетов в случаях аритмии.
Биологические ритмы, биоритмы связаны с тригонометрией
Связь биоритмов с тригонометрией
Модель биоритмов можно построить с помощью графиков тригонометрических функций. Для этого необходимо ввести дату рождения человека ( день, месяц, год ) и длительность прогноза
Движение рыб в воде происходит по закону синуса или косинуса, если зафиксировать точку на хвосте, а потом рассмотреть траекторию движения.
При полёте птицы траектория взмаха крыльев образует синусоиду.
Возникновение музыкальной гармонии
Согласно дошедшим из древности преданиям, первыми, кто попытался сделать это, были Пифагор и его ученики.
Частоты, соответствующие одной и той же ноте в первой, второй и т.д. октавах, относятся, как 1:2:4:8…
диатоническая гамма 2:3:5
Тригонометрия в архитектуре
Детская школа Гауди в Барселоне
Страховая корпорация Swiss Re в Лондоне
Феликс Кандела Ресторан в Лос-Манантиалесе
Интерпретация
Мы привели лишь малую часть того, где можно встретить тригонометрические функции.. Мы выяснили, что тригонометрия была вызвана к жизни необходимостью производить измерения углов, но со временем развилась и в науку о тригонометрических функциях.
Мы доказали, что тригонометрия тесно связана с физикой, встречается в природе, медицине. Можно приводить бесконечно много примеров периодических процессов живой и неживой природы. Все периодические процессы можно описать с помощью тригонометрических функций и изобразить на графиках
Мы думаем, что тригонометрия нашла отражение в нашей жизни, и сферы, в которых она играет важную роль, будут расширяться.
Заключение
Выяснили, что тригонометрия была вызвана к жизни необходимостью производить измерения углов, но со временем развилась и в науку о тригонометрических функциях.
Доказали, что тригонометрия тесно связана с физикой, встречается в природе, музыке, астрономии и медицине.
Думаем, что тригонометрия нашла отражение в нашей жизни, и сферы, в которых она играет важную роль, будут расширяться.
4