Показательная функция (экспонента), ее свойства и график.
0, а≠1, называют показательной функцией. Примеры:" width="640"
Определение
Функцию у=a х , где а0, а≠1, называют показательной функцией.
Примеры:
Область определения показательной функции: D (y)=R – множество всех действительных чисел.
Область значений показательной функции: E (y)=R+ - множество всех положительных чисел.
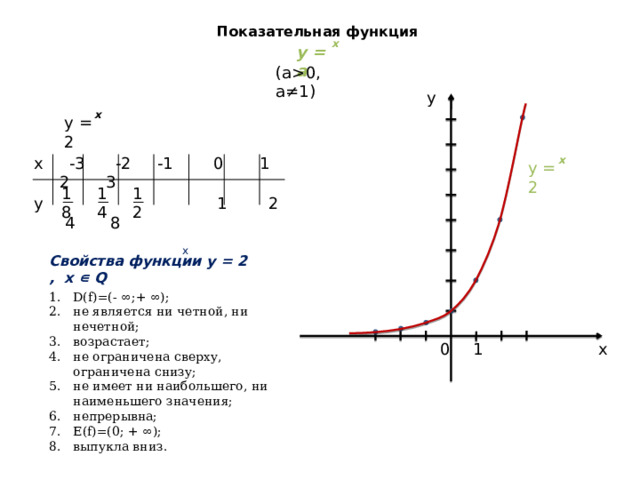0, a≠1) y x y = 2 x x -3 -2 -1 0 1 2 3 y = 2 1 1 1 2 4 8 y 1 2 4 8 x Свойства функции y = 2 , x ∊ Q D(f)=(- ∞;+ ∞); не является ни четной, ни нечетной; возрастает; не ограничена сверху, ограничена снизу; не имеет ни наибольшего, ни наименьшего значения; непрерывна; E(f)=(0; + ∞); выпукла вниз. 1 0 x" width="640"
Показательная функция
x
y = a
(a0, a≠1)
y
x
y = 2
x
x -3 -2 -1 0 1 2 3
y = 2
1
1
1
2
4
8
y 1 2 4 8
x
Свойства функции y = 2 , x ∊ Q
- D(f)=(- ∞;+ ∞);
- не является ни четной, ни нечетной;
- возрастает;
- не ограничена сверху, ограничена снизу;
- не имеет ни наибольшего, ни наименьшего значения;
- непрерывна;
- E(f)=(0; + ∞);
- выпукла вниз.
1
0
x
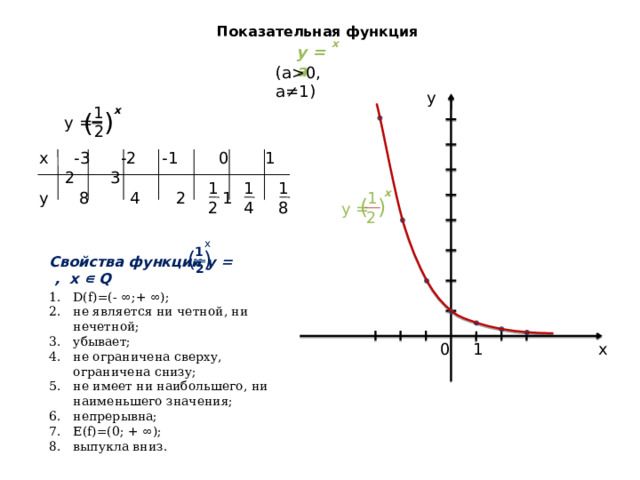0, a≠1) y 1 x ) ( y = 2 x -3 -2 -1 0 1 2 3 1 1 1 8 2 4 x 1 y 8 4 2 1 ) ( y = 2 x 1 ( ) Свойства функции y = , x ∊ Q 2 D(f)=(- ∞;+ ∞); не является ни четной, ни нечетной; убывает; не ограничена сверху, ограничена снизу; не имеет ни наибольшего, ни наименьшего значения; непрерывна; E(f)=(0; + ∞); выпукла вниз. 1 0 x" width="640"
Показательная функция
x
y = a
(a0, a≠1)
y
1
x
)
(
y =
2
x -3 -2 -1 0 1 2 3
1
1
1
8
2
4
x
1
y 8 4 2 1
)
(
y =
2
x
1
(
)
Свойства функции y = , x ∊ Q
2
- D(f)=(- ∞;+ ∞);
- не является ни четной, ни нечетной;
- убывает;
- не ограничена сверху, ограничена снизу;
- не имеет ни наибольшего, ни наименьшего значения;
- непрерывна;
- E(f)=(0; + ∞);
- выпукла вниз.
1
0
x
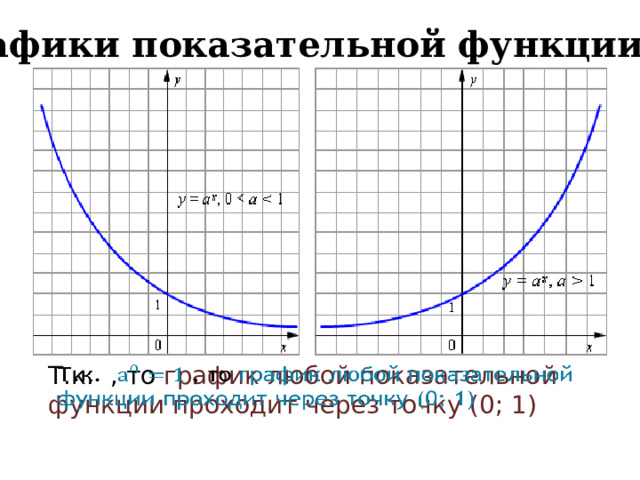
Графики показательной функции:
Т.к. , то график любой показательной функции проходит через точку (0; 1)
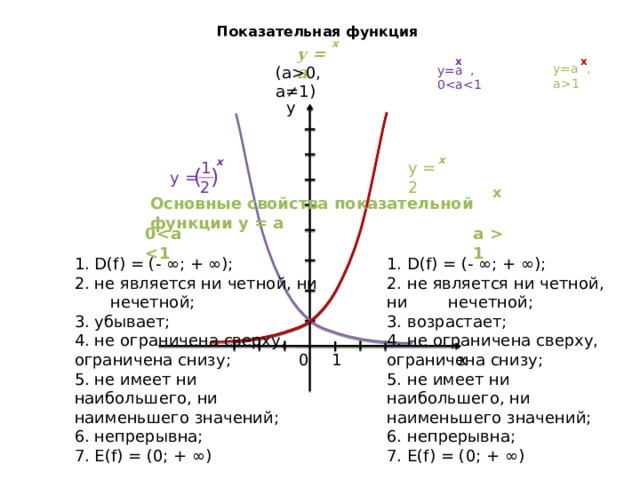1 (a0, a≠1) y=a , 0y x x y = 2 1 ) ( y = 2 x Основные свойства показательной функции y = a a 1 0 1. D(f) = (- ∞; + ∞); 1. D(f) = (- ∞; + ∞); 2. не является ни четной, ни нечетной; 2. не является ни четной, ни нечетной; 3. возрастает; 3. убывает; 4. не ограничена сверху, ограничена снизу; 4. не ограничена сверху, ограничена снизу; 5. не имеет ни наибольшего, ни наименьшего значений; 5. не имеет ни наибольшего, ни наименьшего значений; 6. непрерывна; 6. непрерывна; 7. E(f) = (0; + ∞) 7. E(f) = (0; + ∞) x 1 0 7" width="640"
Показательная функция
x
y = a
x
x
y=a , a1
(a0, a≠1)
y=a , 0
y
x
x
y = 2
1
)
(
y =
2
x
Основные свойства показательной функции y = a
a 1
0
1. D(f) = (- ∞; + ∞);
1. D(f) = (- ∞; + ∞);
2. не является ни четной, ни нечетной;
2. не является ни четной, ни нечетной;
3. возрастает;
3. убывает;
4. не ограничена сверху, ограничена снизу;
4. не ограничена сверху, ограничена снизу;
5. не имеет ни наибольшего, ни наименьшего значений;
5. не имеет ни наибольшего, ни наименьшего значений;
6. непрерывна;
6. непрерывна;
7. E(f) = (0; + ∞)
7. E(f) = (0; + ∞)
x
1
0
7
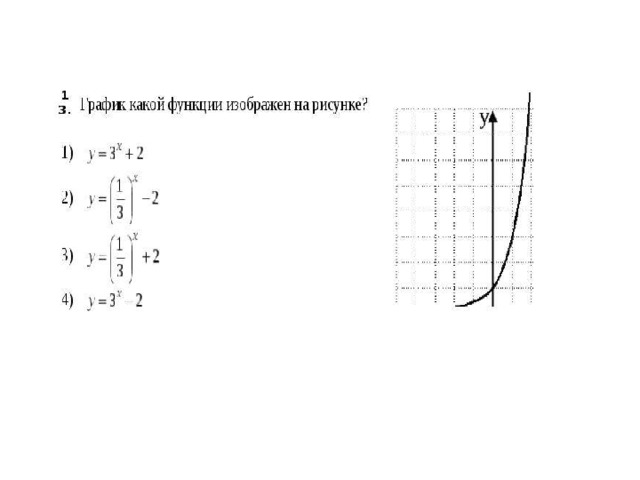
Решить графически уравнение : (построив графики функций левой и правой части уравнения на одном чертеже и определив точку их пересечения)
